浙教版数学八上第2章章末重难点专训 勾股定理的实际运用-最短路径问题
试卷更新日期：2024-08-28 类型：复习试卷
一、选择题
-
1. 如图，圆柱的底面直径为AB，高为AC.一只蚂蚁在C处，沿圆柱的侧面爬到B处，现将圆柱侧面沿AC“剪开”，在侧面展开图上画出蚂蚁爬行的最近路线，正确的是（ ）
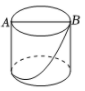A、
B、
C、
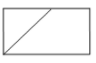D、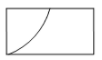
2. 如图，一个圆桶底面直径为8cm，高为12cm，则桶内所能容下的最长木棒的长度为（ ）．
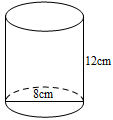A、8cm B、10cm C、 D、3. 如图，有两棵垂直于地面
树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，则它至少要飞行（ ）米．
A、6 B、8 C、10 D、124. 如图，动点P从点A出发，沿着圆柱的侧面移动到BC的中点S ， 若 ， 点P移动的最短距离为5，则圆柱的底面周长为（ ）
A、4 B、4π C、8 D、105. 如图，小明想用彩色胶带装饰他的笔筒，这条胶带沿着这个圆柱的表面，从点A粘贴到点C ， 再从圆柱另外一面粘贴到A ， 已知它的底面直径为6，圆柱高为4，最少要用到的胶带长度为（ ）．
A、 B、 C、 D、6. 如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是（ ）
A、 B、 C、120 D、130二、填空题
-
7. 如图，长方体的上下底面是正方形，底面边长是 ， 高为 ． 在其侧面从点开始，绕侧面两周，嵌入装饰彩条至点停止，则彩条的最短长度为 ．
8. 如图所示，已知圆柱的底面周长为36，高 ， 点位于圆周顶面处，小虫在圆柱侧面爬行，从点爬到点，然后再爬回点，则小虫爬行的最短路程为 ．
9. 如图，长方体的高为 ， 底面长为 ， 宽为 ． 若一只蚂蚁从点爬到 ， 则爬行的最短路程是 ．
10. 如图，在一个长方形草坪上，放着一根长方体的木块，已知米，米，该木块的较长边与平行，横截面是边长为1米的正方形，一只蚂蚁从点A爬过木块到达C处需要走的最短路程是米.
三、解答题
-
11. 如图，学校有一块长方形花圃，且 ， 极少数同学为了避开拐角走“捷径”，在花圃内走出了一条“路”E ， 为此也踩伤了嫩绿的小草．已知m，m，请问他们仅仅少走了多少米？
12. 如图所示的是一个长8 m、宽6 m、高5 m的仓库，在其内壁的A(长的四等分点)处有一只壁虎，B(宽的三等分点)处有一只蚊子，求壁虎爬到蚊子处的最短路程.
13. 一只螳螂在一圆柱形松树树干的点A处，它发现在其正上方的点B处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是按如图所示的路线，绕到虫子后面吃掉它．已知树干的底面周长为20cm，A，B两点间的距离为15cm，求螳螂绕行的最短路程．
14. 如图1，一只蚂蚁要从圆柱的下底面的点爬到上底面的点处，求它爬行的最短距离．已知圆柱底面半径为 ， 高度为 ． 小明同学在研究这个问题时，提出了两种可供选择的方案，方案1：沿爬行；方案2：沿圆柱侧面展开图的线段爬行，如图2．（取3）图1
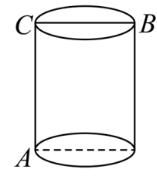图2
(1)、当 ， 时，哪种方式的爬行距离更近？(2)、当 ， 时，哪种方式的爬行距离更近？(3)、当与满足什么条件时，两种方式的爬行距离同样远？四、实践探究题
-
15. 【阅读材料】如图1，有一个圆柱，它的高为12cm，底面圆的周长为18cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，蚂蚁沿圆柱侧面爬行的最短路程是多少?
【方法探究】对于立体图形中求最短路程问题，应把立体图形展开成平面图形，再确定A ， B两点的位置，依据“两点之间线段最短”，结合勾股定理，解决相应的问题．如图2，在圆柱的侧面展开图中，点A ， B对应的位置如图所示，利用勾股定理即可求出蚂蚁爬行的最短路程线段AB的长．
【方法应用】
(1)、如图3，圆柱形玻璃容器的高为18cm，底面周长为60cm，在外侧距下底1cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇，试求急于捕获苍蝇充饥的蜘蛛，所走的最短路线的长度．
(2)、如图4，长方体的棱长 ， ， 假设昆虫甲从盒内顶点开始以的速度在盒子的内部沿棱向下爬行，同时昆虫乙从盒内顶点以相同的速度在盒内壁的侧面上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?