浙教版数学八上第2章特殊三角形三阶单元测试卷

试卷更新日期：2024-08-28 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 如图，长方形 $A B C D$ 的顶点 $A$ ， $B$ 在数轴上，点 $A$ 表示 $- 1$ ， $A B = 3$ ， $A D = 1 .$ 若以点 $A$ 为圆心，对角线 $A C$ 长为半径作弧，交数轴正半轴于点 $M$ ，则点 $M$ 所表示的数为( )

A、 $\sqrt{10} - 1$ B、 $\sqrt{10}$ C、 $\sqrt{10} + 1$ D、 $\sqrt{10} + 2$

查看试题解析
2. 如图，在 Rt $△ A B C$ 中， $∠ A C B = 90^{\circ}$ 。若 $A B = 10$ ，则正方形 $A D E C$ 和正方形 $B C F G$ 的面积和为 ( )

A、80 B、100 C、200 D、无法确定

查看试题解析
3. 如图有两棵树，一棵高，一棵矮，两树之间相距，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了 $()$ 米？

A、 $11$ B、 $12$ C、 $13$ D、 $14$

查看试题解析
4. $△ A B C$ 的三边分别为 $a$ ， $b$ ， $c$ ，下列条件：
$① ∠ A = ∠ B - ∠ C$ ； $② a^{2} = (b + c) (b - c)$ ； $③ a$ ： $b$ ： $c = 3$ ： $4$ ： $5$ ．
其中能判断 $△ A B C$ 是直角三角形的条件个数有( )

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析
5. 如图，直线 $l_{1} / / l_{2}$ ，以直线 $l_{1}$ 上的点 $A$ 为圆心，适当长为半径画弧，分别交直线 $l_{1} 和 l_{2} 于 B 、 C$ 两点，连接 $A C 、 B C$ ，若 $∠ A B C = 65 °$ ，则 $∠ 1$ 的度数是( )

A、 $35 °$ B、 $50 °$ C、 $65 °$ D、 $70 °$

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD，CE是 $△ A B C$ 的两条中线，P是AD上的一个动点，则下列线段的长等于 $B P + E P$ 最小值的是（）

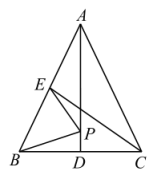A、AC B、BC C、AD D、CE

查看试题解析
7. 如图，在四边形 $A B C D$ 中， $∠ A = ∠ B C D = 60 °$ ， $B C = C D$ ， $C M ⊥ A B$ 交 $A B$ 的延长线于点M ， $C N ⊥ A D$ 交 $A D$ 的延长线于点N ．若 $2 B M = 3 D N$ ， $A D = k A B$ ，则常数k的值为（）

A、 $\frac{9}{8}$ B、 $\frac{8}{7}$ C、 $\frac{7}{6}$ D、 $\frac{6}{5}$

查看试题解析
8. 如图，在 $Δ A B C$ 中， $∠ C = 90^{\circ}$ ， $∠ B = 30^{\circ}$ ，以 $A$ 为圆心，任意长为半径画弧分别交 $A B$ 、 $A C$ 于点 $M$ 和 $N$ ，再分别以 $M$ 、 $N$ 为圆心，大于 $M N$ 的长为半径画弧，两弧交于点 $P$ ，连结 $A P$ 并延长交 $B C$ 于点 $D$ ，则下列说法中正确的个数是（）
① $A D$ 是 $∠ B A C$ 的平分线；② $∠ A D C = 60^{\circ}$ ；③ $D A = D B$ ；④ $S_{Δ D A C} = S_{Δ A B C} = 1 ： 2$

A、1 B、2 C、3 D、4

查看试题解析
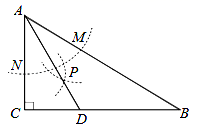9. 在 $△ A B C$ 中，已知 $∠ B A C = 9 0^{°} ， A B \neq A C$ ，若用无刻度的直尺和圆规在BC上找一点 $D$ ，使 $△ A C D$ 是等腰三角形，则下列作法中，正确的有（）

A、②③ B、①② C、①③ D、①②③

查看试题解析
10. 如图，BD平分∠_ABC，且∠BEC=∠BCE，D为BE延长线上的一点，BD= BA，过D作DG⊥AB，垂足为G．下列结论：①△ABE≌△DBC；②∠BCE+∠BCD= 180°；③AD= AE= DG；④BA+BC=2BG．其中正确的是（）

A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 如图，在边长为4的等边△ABC中，射线BD⊥AC于点D，将△ABD沿射线BD平移，得到△EGF，连接CF、CG，则CF+CG的最小值为.

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ C = 30 °$ ，点 $D$ 是 $A C$ 的中点， $D E ⊥ A C$ 交 $B C$ 于 $E$ ；点 $O$ 在 $D E$ 上， $O A = O B$ ， $O D = 1$ ， $O E = 2$ ，则 $B E$ 的长为．

查看试题解析
13. 如图， $A B ∥ C D ， ∠ C = 60^{\circ} ， E$ 是射线 $C D$ 上一点，连结 $A E$ ，将三角形 $A E C$ 沿着 $A E$ 翻折得到三角形 $A E F$ ，点 $C$ 的对应点为点 $F$ ，若 $∠ E A F = \frac{7}{6} ∠ F A B$ ，则 $∠ A E C =$

查看试题解析
14. 如图，等腰 $△ A B C$ 的底边 $B C = 12$ ，面积为48，点 $F$ 在边 $B C$ 上，且 $B F = 3 F C$ ， $E G$ 是腰 $A C$ 的垂直平分线，若点 $D$ 在 $E G$ 上运动，则 $△ C D F$ 周长的最小值为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A < 90^{\circ}$ ，点 $D ， E ， F$ 分别在边 $A B ， B C ， C A$ 上，连结 $D E ， E F ， F D$ ，已知点 $B$ 和点 $F$ 关于直线 $D E$ 对称．设 $\frac{B C}{A B} = k$ ，若 $A D = D F$ ，则 $\frac{C F}{F A} =$ (结果用含 $k$ 的代数式表示)．

查看试题解析
16. 如图，有一直角三角形纸片 $A B C$ ， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $A C = 1$ ， $C D ⊥ A B$ 于点 $D$ ． $F$ ， $G$ 分别是线段 $A D$ ， $B D$ 上的点， $H$ ， Ⅰ分别是线段 $A C$ ， $B C$ 上的点，沿 $H F$ ， $G I$ 折叠，使点 $A$ ， $B$ 恰好都落在线段 $C D$ 上的点 $E$ 处．当 $F G = E G$ 时， $A F$ 的长是．

查看试题解析

三、解答题（本题共8小题，第17题6分，第18题6分，第19题8分，第20题11分，第21题8分，第22题8分，第23题7分，第24题10分，共66分）

17. 如图，在四边形 $A B C D$ 中，已知 $∠ A C D = 90 °$ ， $C D = 2$ ， $A D = 2 \sqrt{2}$ ， $B C = 1$ ， $A B = \sqrt{3}$ ．

(1)、判断 $△ A B C$ 是直角三角形吗？请说明理由．

(2)、连接 $B D$ ，求 $△ B C D$ 的面积．

查看试题解析
18. 已知 $△ A B C$ 为等边三角形， $D$ 是边 $A B$ 上一点，连接 $C D$ ，点 $E$ 为 $C D$ 上一点，连接 $B E$ ．
图1 图2 图3

(1)、如图1，延长 $B E$ 交 $A C$ 于点 $F$ ，若 $∠ C B F = 45 °$ ， $B F = 3 \sqrt{2}$ ，求 $C F$ 的长；

(2)、如图2，将 $△ B E C$ 绕点 $C$ 顺时针旋转 $60 °$ 到 $△ A G C$ ，延长 $B C$ 至点 $H$ ，使得 $C H = B D$ ，连接 $A H$ 交 $C G$ 于点 $N$ ，求证 $C E = D E + 2 G N$ ；

(3)、如图3， $A B = 8$ ，点 $H$ 是 $B C$ 上一点，且 $B D = 2 C H$ ，连接 $D H$ ，点 $K$ 是 $A C$ 上一点， $C K = A D$ ，连接 $D K$ ， $B K$ ，将 $△ B K D$ 沿 $B K$ 翻折到 $△ B K Q$ ，连接 $C Q$ ，当 $△ A D K$ 的周长最小时，直接写出 $△ C K Q$ 的面积．

查看试题解析
19. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 10 c m$ ， $B C = 6 c m$ ，若动点 $P$ 从点 $C$ 开始，按 $C \to A \to B \to C$ 的路径运动，且速度为每秒 $2 c m$ ，设出发的时间 $t$ 秒．

(1)、出发2秒后，求 $△ A B P$ 周长；

(2)、求当 $t$ 为何值时， $△ B C P$ 为等腰三角形．

(3)、另有一点 $Q$ ，从点 $C$ 开始，按 $C \to A \to B \to C$ 的路径运动，且速度为每秒 $8 c m$ ，若 $P 、 Q$ 两点同时出发，当 $P 、 Q$ 中有一点到达终点时，另一点也停止运动．当 $t$ 为何值时，直线 $P Q$ 把 $△ A B C$ 的周长分成相等的两部分？

查看试题解析
20. 实验学校数学兴趣小组对特殊三角形外一点与该三角形三个顶点所形成的线段数量关系展开探究：

(1)、如图①，已知等边三角形 $A B C$ 边 $C B$ 的延长线上一点P ，且满足 $∠ A P B = 30 °$ ，求线段 $P A$ 、 $P B$ 、 $P C$ 的数量关系，马超同学一眼看出结果为， $P A^{2} + P B^{2} = P C^{2}$ ，你是否同意，请聪明的你说明理由；

(2)、在探究过程中，小组同学们发现，当点P不在任意边的延长线上时，所形成的图形形似“鸡爪”，于是兴趣小组同学们对“鸡爪”图形的特点展开深入探究：如图②， $△ A B C$ 为等边三角形， $∠ A P B = 30 °$ ，（1）中的结论是否仍成立？小孙同学是这样做的：首先将线段 $A P$ 朝外作等边三角形 $A P D$ ，连接 $B D$ ， $P C$ ……，请沿着小孙同学的思路尝试着走下去看看结论是否符合（1）中的结论；

(3)、如图③，“鸡爪”图形 $P A C B$ 中， $△ A B C$ 是等腰直角三角形， $∠ B A C = 90 °$ ， $∠ A P B = 45 °$ ，请简述线段 $P A$ 、 $P B$ 、 $P C$ 的的数量关系；

(4)、如图④，“鸡爪”图形 $P A C B$ 中， $△ A B C$ 是等腰直角三角形， $∠ B A C = 90 °$ ， $∠ A P B = 45 °$ ，若 $P B = 1$ ， $P C = 2$ ，请直接写出 $P A$ 的长．

查看试题解析
21. 某研究性学习小组在学习第三章第4节《简单的图案设计》时，发现了一种特殊的四边形，如图1，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B + ∠ D = 180 °$ ，我们把这种四边形称为“等补四边形”．如何求“等补四边形”的面积呢？

(1)、探究一：
如图2，已知“等补四边形” $A B C D$ ，若 $∠ A = 90 °$ ，将“等补四边形” $A B C D$ 绕点 $A$ 顺时针旋转 $90 °$ ，可以形成一个直角梯形（如图3）．若 $B C = 4 c m$ ， $C D = 2 c m$ ，则“等补四边形”的面积为 $c m^{2}$

(2)、探究二：
如图4，已知“等补四边形” $A B C D$ ，若 $∠ A = 120 °$ ，将“等补四边形”绕点 $A$ 顺时针旋转 $120 °$ ，再将得到的四边形按上述方式旋转 $120 °$ ，可以形成一个等边三角形（如图5）．若 $B C = 6 c m$ ， $C D = 4 c m$ ，求“等补四边形” $A B C D$ 的面积．

(3)、探究三：
由以上探究可知，对一些特殊的“等补四边形”，只需要知道 $B C$ ， $C D$ 的长度，就可以求它的面积．那么如图6，已知“等补四边形” $A B C D$ ，连接 $A C$ ，若 $B C = m$ ， $C D = n$ ， $∠ A C D = 30 °$ ，试求出“等补四边形” $A B C D$ 的面积（用含 $m$ ， $n$ 的代数式表示）．

查看试题解析
22. 在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是直线 $B C$ 上一点 $($ 不与 $B$ 、 $C$ 重合 $)$ ，以 $A D$ 为一边在 $A D$ 的右侧作 $△ A D E$ ，使 $A D = A E$ ， $∠ D A E = ∠ B A C$ ，连接 $C$ E ．

(1)、如图1，当点 $D$ 在线段 $B C$ 上，如果 $∠ B A C = 90 °$ ．

①则 $△ A B D$ 与 $△ A C E$ 全等吗？请说明理由；
②求 $∠ B C E$ 的度数；

(2)、如图2，如果 $∠ B A C = 60 °$ ，当点 $D$ 在线段 $B C$ 上移动，则 $∠ B C E$ 的度数是 $°$ ；

(3)、如图2，当点 $D$ 在线段 $B C$ 上，如果 $∠ B A C = 60 °$ ， $D$ 点为 $△ A B C$ 中 $B C$ 边上的一个动点 $(D$ 与 $B$ 、 $C$ 均不重合 $)$ ，当点 $D$ 运动到什么位置时， $△ D C E$ 的周长最小？

查看试题解析
23. 在 $△ A B C$ 中， $A B = A C$ ， $D$ 是直线 $A B$ 上一动点（不与点 $A$ ， $B$ 重合）．

(1)、如图1，若 $∠ A < 90 °$ ，点 $D$ 在边 $A B$ 上， $D E ⊥ A B$ 交 $B C$ 于点 $E$ ， $E F ⊥ B C$ 交 $A C$ 于点 $F$ ．若 $∠ A F E = 155 °$ ，求 $∠ D E F$ 的度数．

(2)、如图2，若 $∠ B A C = 90 °$ ，点 $D$ 在边 $A B$ 上， $B E ⊥ C D$ ，交直线 $C D$ 于点 $E$ ，交直线 $A C$ 于点 $F$ ．
①线段 $A B$ ， $A F$ ， $B D$ 三者之间的数量关系是 ▲ ；

②若点 $D$ 在 $A B$ 的延长线①中的结论是否成立？若成立，请给出推理过程；若不成立，请画出图形，并直接写出 $A B$ ， $A F$ ， $B D$ 三者之间的数量关系．

③若点 $D$ 在边 $A B$ 上，且 $C D = 2 B E$ ，请判断 $A B$ ， $A F$ ， $B C$ 三者之间的数量关系，并说明理由．

查看试题解析
24. 已知线段 $A B$ 垂直直线 $l$ 于点 $B$ ，点 $D$ 在直线 $l$ 上，分别以 $A B$ ， $A D$ 为边作等边三角形 $A B C$ （点 $C$ 在边 $A B$ 的右侧）和等边三角形 $A D E$ ，直线 $C E$ 交直线 $l$ 于点 $F$ ．

(1)、当点 $F$ 在线段 $B D$ 上时，如图1，求证： $C E = C F + D F$ ；

(2)、①当点 $F$ 在线段 $B D$ 的延长线上时（如图2），请直接写出线段 $C E$ ， $C F$ ， $D F$ 之间的数量关系；
②当点 $F$ 在线段 $D B$ 的延长线上时（如图3），请直接写出线段 $C E$ ， $C F$ ， $D F$ 之间的数量关系；
③在①和②中，选择其中一个进行证明；

(3)、当 $B D = 3 B F$ ，且 $E F = 16$ 时，请直接写出 $A B$ 的长．

查看试题解析

浙教版数学八上第2章 特殊三角形 三阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题6分，第18题6分，第19题8分，第20题11分，第21题8分，第22题8分，第23题7分，第24题10分，共66分）

浙教版数学八上第2章特殊三角形三阶单元测试卷