浙教版数学八上第2章特殊三角形二阶单元测试卷

试卷更新日期：2024-08-28 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 下列长度的三条线段，能成为一个直角三角形的三边的一组是（　　）

A、 $\sqrt{3} ， \sqrt{4} ， \sqrt{5}$ B、1，2， $\sqrt{3}$ C、2，4， $\sqrt{6}$ D、9，16，25

查看试题解析
2. 若3、4、a为勾股数，则a的值为（）

A、 $\sqrt{7}$ B、5 C、5或7 D、5或 $\sqrt{7}$

查看试题解析
3. 中华文明，源远流长：中华汉字，寓意深广．下列四个选项中，是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
4. 有六根细木棒，它们的长度分别是2，4，6，8，10，12（单位：cm），从中取出三根首尾顺次连接搭成一个直角三角形，则这三根木棒的长度分别为（）

A、2，4，8 B、4，8，10 C、6，8，10 D、8，10，12

查看试题解析
5. 我国是最早了解勾股定理的国家之一，在《周髀算经》中记载了勾股定理的公式与证明，相传是由商高发现，故又称之为“商高定理”．下列四幅图中，不能证明勾股定理的是（）

A、 B、 C、 D、

查看试题解析
6.
如图，矩形纸片ABCD中，点E是AD的中点，且AE=1，连接BE，分别以B、E为圆心，以大于 $\frac{1}{2}$ BE的长为半径作弧，两弧交于点M、N，若直线MN恰好过点C，则AB的长度为（　　）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、2

查看试题解析
7. 如图所示的衣架可以近似看成一个等腰三角形 $A B C$ ，其中 $A B = A C$ ， $A D ⊥ B C$ 于点 $D$ ，若 $A C = 60 c m, ∠ B = 3 0^{∘}$ ，则下列说法正确的是（）

A、 $B C = 40 c m$ B、 $A D = 30 c m$ C、 $∠ C A D = 3 0^{∘}$ D、 $∠ B A C = 10 0^{∘}$

查看试题解析
8. 如图，每个小正方形的边长都相等， $A, B, C$ 是小正方形的顶点，则 $∠ A B C$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $50 °$ D、 $60 °$

查看试题解析
9. 如图，在等边 $△ A B C$ 中， $A B = 3$ ， D ， E分别是边 $B C$ ， $C A$ 上的动点，且 $B D = C E$ ，连接 $A D$ ， $B E$ 交于点F ，在点D从点B运动到点C的过程中，图中阴影部分的面积的最小值为（）

A、 $\frac{3 \sqrt{3}}{8}$ B、 $\frac{3 \sqrt{3}}{4}$ C、 $\frac{3}{8}$ D、 $\frac{1}{3}$

查看试题解析
10. 如图， $O$ 是等边 $△ A B C$ 内一点， $O A = 6, O B = 8, O C = 10$ ，将线段 $B O$ 以点 $B$ 为旋转中心逆时针旋转 $60 °$ 得到线段 $B O^{'}$ ，下列结论：① $△ B O^{'} A$ 可以由 $△ B O C$ 绕点 $B$ 逆时针旋转 $60 °$ 得到；②点 $O$ 与 $O^{'}$ 的距离为6；③ $∠ A O B = 150 °$ ；④ $S_{四边形 A O B O^{'}} = 24 + 12 \sqrt{3}$ ；⑤ $S_{△ B O C} = 12 + 16 \sqrt{3}$ ．其中正确的结论有（）个

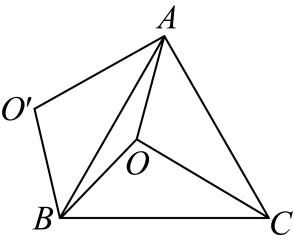A、5 B、4 C、3 D、2

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 一个直角三角形的两条边长分别为4和5，则第三边长为.

查看试题解析
12. 等腰三角形的一个内角是 $70 °$ ，则它底角的度数是．

查看试题解析
13. 如图，一块形如“Z”字形的铁皮，每个角都是直角，且AB＝BC＝EF＝GF＝1，CD＝DE＝GH＝AH＝3，则AF＝.

查看试题解析
14. 如图，阴影部分表示以 $R t △ A B C$ 的各边为直径的三个半圆所组成的两个新月形，面积分别记作 $S_{1}$ 和 $S_{2}$ .若 $S_{1} + S_{2} = 14$ ， AB=5，则 $△ A B C$ 的周长是.

查看试题解析
15. 如图， $R t ∆ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C = 4$ ，点 $E$ 为 $A B$ 边上一点， $A E = 3$ ，点 $D$ 为 $B C$ 边的中点，连接 $A D$ ，点 $F$ 为线段 $A D$ 上的动点，连接 $F E, F B$ ，则 $F E + F B$ 的最小值为．

查看试题解析
16. 如图，等边 $△ A B C$ 的边长为6，D是 $B C$ 的中点，E是 $A C$ 边上的一点，连接 $D E$ ，以 $D E$ 为边作等边 $△ D E F$ ，若 $C E = 2$ ，则线段 $A F$ 的长为．

查看试题解析

三、解答题（本题共8小题，第17题6分，第18题6分，第19题6分，第20题8分，第21题8分，第22题10分，第23题10分，第24题12分，共66分）

17. 如图，连接四边形ABCD的对角线AC，已知∠B＝90°，BC＝1，∠BAC＝30°，CD＝2，AD＝2 $\sqrt{2}$ .

(1)、求证：△ACD是直角三角形；

(2)、求四边形ABCD的面积．

查看试题解析
18. 如图，在4x3正方形网格中，每个小正方形的边长都是1．

(1)、分别求出线段AB、CD的长度；

(2)、在图中画出线段EF、使得EF的长为 $\sqrt{5}$ ，以AB、CD、EF三条线段能否构成直角三角形，并说明理由.

查看试题解析
19. “儿童散学归来早，忙趁东风放纸鸢” $.$ 又到了放风筝的最佳时节．某校八年级 $(1)$ 班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E ($ 如图 $)$ ，他们进行了如下操作： $①$ 测得水平距离 $B D$ 的长为 $8$ 米； $②$ 根据手中剩余线的长度计算出风筝线 $B C$ 的长为 $17$ 米； $③$ 牵线放风筝的小明的身高为 $1.5$ 米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降 $9$ 米，则他应该往回收线多少米？

查看试题解析
20. 在综合与实践课上，老师让同学们以“两条平行线AB ， CD和一块含 $60 °$ 角的直角三角尺EFG（ $∠ E F G = 90 °$ ， $∠ E G F = 60 °$ ）”为主题开展数学活动．

(1)、如图（1），若三角尺的 $60 °$ 角的顶点G放在CD上，若 $∠ 2 = 2 ∠ 1$ ，求 $∠ 1$ 的度数；

(2)、如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明 $∠ A E F$ 与 $∠ F G C$ 间的数量关系．

查看试题解析
21. 阅读与思考
如图 1 所示的是一座钢铁桥梁，为了计算其中一个三角形钢架的面积，小明想办法测量出三边的长度 $A B = c = 24$ 米， $B C = a = 26$ 米， $A C = b = 28$ 米，如何求三角形 $A B C$ 钢架的面积?下面是甲，乙两位同学的解题思路，分别根据甲、乙两位同学的解题思路求 $△ A B C$ 的面积.

(1)、甲同学：我们知道，已知 $△ A B C$ 的三边长 $a, b, c$ ，设 $p = \frac{1}{2} (a + b + c)$ ，即 $p$ 为 $△ A B C$ 周长的一半，那么利用海伦公式 $S_{△ A B C} = \sqrt{p (p - a) (p - b) (p - c)}$ 就可求出 $△ A B C$ 的面积.

(2)、乙同学：如图 2 ，过点 $A$ 作 $A D ⊥ B C$ 于点 $D$ ，设BD=x米，然后用含 $x$ 的代数式表示出 $C D$ ，根据勾股定理，利用 $A D$ 作为“桥梁”建立方程，利用勾股定理求出 $A D$ 的长，再计算 $Δ A B C$ 的面积.

查看试题解析
22. 如图，一个梯子 $A B$ 长25米，顶端 $A$ 靠在墙 $A C$ 上（墙与地面垂直），这时梯子下端 $B$ 与墙角 $C$ 距离为7米．

(1)、求梯子顶端 $A$ 与地面的距离 $A C$ 的长；

(2)、若梯子的顶端 $A$ 下滑到 $E$ ，使 $A E = 4$ ，求梯子的下端 $B$ 滑动的距离 $B D$ 的长．

查看试题解析
23. 已知 $A M ∥ C N ， B$ 为平面内一点， $A B ⊥ B C$ 于点 $B$ ．

(1)、如图 1 所示，直接写出 $∠ A$ 和 $∠ C$ 之间的数量关系．

(2)、如图 2 所示，过点 $B$ 作 $B D ⊥ A M$ 于点 $D$ ，求证： $∠ A B D = ∠ C$ ．

(3)、如图 3 所示，在 (2) 问的条件下，点 $E ， F$ 在 $D M$ 上，连结 $B E ， B F ， C F ， B F$ 平分 $∠ D B C ， B E$ 平分 $∠ A B D$ ，若 $∠ F C B + ∠ N C F = 180^{\circ} ， ∠ B F C = 3 ∠ D B E$ ，求 $∠ E B C$ 的度数．

查看试题解析
24. 在 $△ A B C$ 中， $∠ B = 40 °$ ， $∠ A C B = 110 °$ ， $D$ 为边 $B C$ 延长线上一点，连接 $A D$ ．

(1)、如图1，当 $∠ D = ∠ B$ 时，求证： $A B = C D$ ；

(2)、如图2，当 $∠ D = 2 ∠ B$ 时，求证： $A B = A D + C D$ ；、

(3)、如图3，当 $A B = C D$ 时，求证： $∠ D = ∠ B$ ．

查看试题解析

浙教版数学八上第2章 特殊三角形 二阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题6分，第18题6分，第19题6分，第20题8分，第21题8分，第22题10分，第23题10分，第24题12分，共66分）

浙教版数学八上第2章特殊三角形二阶单元测试卷