浙教版数学八上第2章特殊三角形一阶单元测试卷

试卷更新日期：2024-08-28 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 以下是回收、绿色包装、节水、低碳四个标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各组数中，能构成直角三角形的是（）

A、4，5，6 B、1，1， $\sqrt{2}$ C、6，8，11 D、5，12，23

查看试题解析
3. $R t △ A B C$ 中， $∠ C = 90 ° ， ∠ B - ∠ A = 30 °$ ，则 $∠ B$ 的度数为（）

A、50° B、60° C、70° D、80°

查看试题解析
4. 一根旗杆在离地面3米处断裂，旗杆顶部落在离旗杆底部4米处，旗杆折断之前的高度是（）

A、5米 B、7米 C、8米 D、9米

查看试题解析
5. 如图，已知AB⊥CD ， △ABD ， △BCE都是等腰直角三角形，如果CD=8，BE=3，则AC等于（）

A、8 B、5 C、3 D、 $\sqrt{34}$

查看试题解析
6. 如图所示的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，则点A到BC的距离等于（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、 $\frac{4}{\sqrt{10}}$ D、 $\frac{2}{\sqrt{10}}$

查看试题解析
7. 如图，在四边形ABCD中，∠ABC＝∠CDA＝90°，分别以四边形ABCD的四条边为边长，向外作四个正方形，面积分别为S₁ ， S₂ ， S₃和S₄ ．若S₁＝2，S₂＝8，S₄＝3，则S₃的值是（）

A、8 B、7 C、6 D、5

查看试题解析
8. 已知 $△$ ABC的三边长a，b，c满足（a﹣b）（c²﹣a²﹣b²）＝0，则 $△$ ABC的形状是（）

A、等腰三角形或直角三角形 B、等腰直角三角形 C、等腰三角形 D、直角三角形

查看试题解析
9. 如图，在 $△ D E F$ 中， $∠ D = 90 °$ ， $D G ： G E = 1 ： 3$ ， $G E = G F$ ， Q是 $E F$ 上一动点，过点Q作 $Q M ⊥ D E$ 于M ， $Q N ⊥ G F$ 于N ， $E F = 4 \sqrt{3}$ ，则 $Q M + Q N$ 的长是（）

A、 $4 \sqrt{3}$ B、 $3 \sqrt{2}$ C、4 D、 $2 \sqrt{3}$

查看试题解析
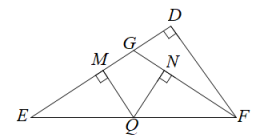10. 如图，在△ABC中，AD为∠BAC的平分线，BM⊥AD，垂足为M，且AB=5，BM=2，AC=9，则∠ABC与∠C的关系为（）

A、∠ABC=2∠C B、∠ABC= $\frac{5}{2}$ ∠C C、 $\frac{1}{4}$ ∠ABC=∠C D、∠ABC=3∠C

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 命题“两直线平行，同位角相等．”的逆命题是．

查看试题解析
12. 在 $R t △ A B C$ 中， $D$ 是斜边 $A B$ 的中点，若 $A B = 13$ ，则 $D C$ 的长是．

查看试题解析
13. 写出一组勾股数．

查看试题解析
14. 如图，网格中每个小正方形的边长均为 $1$ ，以 $A$ 为圆心， $A B$ 为半径画弧，交网格线于点 $D$ ，则 $E D$ 的长为．

查看试题解析
15. 如图，已知P是∠AOB平分线上一点， $∠ A O P = 15 °$ ， $C P / / O B$ 交 $O A$ 于点 $C$ ， $P D ⊥ O B$ ，垂足为 $D$ ，且 $P C = 6$ ，则△OPC的面积等于．

查看试题解析
16. 如图， $△ ABC$ 中， $AB = AC$ ， $∠ BAC = 54^{\circ}$ ，点 $D$ 为 $AB$ 中点，且 $OD ⊥ AB$ ， $∠ BAC$ 的平分线与 $AB$ 的垂直平分线交于点 $O$ ，将 $∠ C$ 沿 $EF$ （ $E$ 在 $BC$ 上， $F$ 在 $AC$ 上）折叠，点 $C$ 与点 $O$ 恰好重合，则 $∠ OEC$ 为度.

查看试题解析

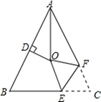
三、解答题（本题共8小题，第17题6分，第18题6分，第19题6分，第20题7分，第21题10分，第22题12分，第23题7分，第24题12分，共66分）

17. 已知一个直角三角形的两条直角边长分别为 $\sqrt{7} + \sqrt{3}$ 和 $\sqrt{7} - \sqrt{3}$ . 求这个直角三角形的斜边长和面积.

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $A B = 16$ ， $B C = 12$ ， $A D = 21$ ， $C D = 29$ ．求四边形 $A B C D$ 的面积．

查看试题解析
19. 如图所示，E，F分别是等边三角形ABC的边AB，AC上的点，且BE=AF，CE，BF交于点P.

(1)、试说明：BF=CE；

(2)、求∠BPC的度数.

查看试题解析

20. 综合与实践

某实践探究小组在放风筝时想测量风箏离地面的垂直高度，通过勘测，得到如下记录表：

测量示意图
测量数据	边的长度	①测得水平距离 $B C$ 的长为15米．
		②根据手中剩余线的长度计算出风筝线 $A B$ 的长为17米．
		③小明牵线放风筝的手到地面的距离为1.7米．

数据处理组得到上面数据以后做了认真分析，他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度 $A D$ ．请完成以下任务．

(1)、已知：如图，在

R t △ A B C

中，

∠ A C B = 90 °

，

B C = 15

，

A B = 17

．求线段

A D

的长．

(2)、如果小明想要风筝沿

D A

方向再上升12米，

B C

长度不变，则他应该再放出多少米线？

查看试题解析

21. 如图1所示，D，E，F分别是 $△ A B C$ 的三边 $A B$ ， $B C$ 和 $A C$ 上的点，若 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ， $∠ 5 = ∠ 6$ ，则称 $△ D E F$ 为 $△ A B C$ 的反射三角形．

(1)、如图2所示，若 $△ A B C$ 是等边三角形，猜想其反射三角形的形状，并画出图形．

(2)、如图3所示，若 $△ D E F$ 是 $△ A B C$ 的反射三角形， $∠ B = ∠ C$ ， $∠ A = 50 °$ ，求 $△ D E F$ 各个角的度数．

(3)、利用图1探究：
① $△ A B C$ 的三个内角与其反射三角形 $D E F$ 的对应角（如 $∠ D E F$ 与 $∠ A$ ）之间的数量关系．
②在直角三角形和钝角三角形中，是否存在反射三角形？如果存在，说出其反射三角形的形状；如果不存在，请说明理由．

查看试题解析
22. 今年第6号台风“烟花”登录我国沿海地区，风力强，累计降雨量大，影响范围大，有极强的破坏力.如图，台风“烟花”中心沿东西方向AB由A向B移动，已知点C为一海港，且点C与直线AB上的两点A、B的距离分别为AC＝300km，BC＝400km，又AB＝500km，经测量，距离台风中心260km及以内的地区会受到影响.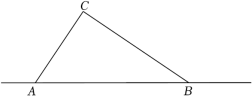

(1)、求∠ACB的度数；

(2)、海港C受台风影响吗？为什么？

(3)、若台风中心的移动速度为28千米/时，则台风影响该海港持续的时间有多长？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ， D为 $A C$ 的中点， $D E ⊥ A B$ 于点E ， $D F ⊥ B C$ 于点F ，且 $D E = D F$ ，连接 $B D$ ，点G在 $B C$ 的延长线上，且 $C D = C G$ ．

(1)、求证： $△ A B C$ 是等边三角形；

(2)、若 $B F = 3$ ，求 $C G$ 的长．

查看试题解析
24. 如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．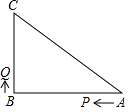

(1)、当t=2秒时，求PQ的长；

(2)、求出发时间为几秒时，△PQB是等腰三角形？

(3)、若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析

浙教版数学八上第2章 特殊三角形 一阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题6分，第18题6分，第19题6分，第20题7分，第21题10分，第22题12分，第23题7分，第24题12分，共66分）

浙教版数学八上第2章特殊三角形一阶单元测试卷