【培优版】浙教版数学八上2.8 直角三角形的判定同步练习
试卷更新日期:2024-08-27 类型:竞赛测试
一、选择题
-
1. 如图,在△ABC中,∠C=90°,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( )
2. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( ) A、①②③ B、①②④ C、①③④ D、②③④3. 如图,在中, , 是的平分线,于点E , 平分 , 则等于( )
A、①②③ B、①②④ C、①③④ D、②③④3. 如图,在中, , 是的平分线,于点E , 平分 , 则等于( ) A、 B、 C、 D、4. 如图,点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上②点P在∠CBE的平分线上③点P在∠BCD的平分线上 ④点P是 ∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )
A、 B、 C、 D、4. 如图,点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上②点P在∠CBE的平分线上③点P在∠BCD的平分线上 ④点P是 ∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )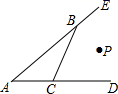 A、①②③ B、①②③④ C、②③ D、④5. 如图, 在 Rt 中, 的平分线 A E 交 B C 于点 于点 , 若 的周长为 12 , 则 的周长为 4 , 则 A C 为 ( )
A、①②③ B、①②③④ C、②③ D、④5. 如图, 在 Rt 中, 的平分线 A E 交 B C 于点 于点 , 若 的周长为 12 , 则 的周长为 4 , 则 A C 为 ( ) A、3 B、4 C、6 D、86. 如图,点 是 的中点,平分 , 下列结论:①;②;③;④ , 四个结论中成立的是( )
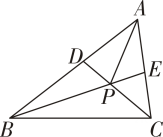
A、3 B、4 C、6 D、86. 如图,点 是 的中点,平分 , 下列结论:①;②;③;④ , 四个结论中成立的是( ) A、①②④ B、①②③ C、③④ D、①③7. 如图,任意画一个的△ABC , 再分别作△ABC的两条角平分线BE和CD , BE和CD相交于点P , 连接AP , 以下结论:
A、①②④ B、①②③ C、③④ D、①③7. 如图,任意画一个的△ABC , 再分别作△ABC的两条角平分线BE和CD , BE和CD相交于点P , 连接AP , 以下结论:①;②AP平分∠BAC;③;④;⑤ ,
正确的有( )
 A、5个 B、4个 C、3个 D、2个8. 如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( )
A、5个 B、4个 C、3个 D、2个8. 如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. 如图,在△ABC中,D为AB中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥BC交AC于点F,AC=8,BC=12,则BF的长为.
 10. 如图,在中,是高, , , 在边上取点 , 连接 , , 若 , , 则 .
10. 如图,在中,是高, , , 在边上取点 , 连接 , , 若 , , 则 . 11. 如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为.
11. 如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为.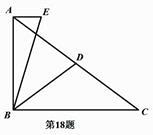 12. 如图,已知等边和等边 , 点P在BC的延长线上,EC的延长线交AP于点M,连接BM;下列结论:①;②;③BM平分;④ , 其中正确的有(填序号).
12. 如图,已知等边和等边 , 点P在BC的延长线上,EC的延长线交AP于点M,连接BM;下列结论:①;②;③BM平分;④ , 其中正确的有(填序号).
三、解答题
-
13. 如图,在和中, , , , 延长 , 交于点 .
 (1)、求证:平分;(2)、若 , , , 求的长.14. 如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一点,连接BD,EC⊥AC,且AE=BD,连接AE交BC于点F,交BD于点H.
(1)、求证:平分;(2)、若 , , , 求的长.14. 如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一点,连接BD,EC⊥AC,且AE=BD,连接AE交BC于点F,交BD于点H. (1)、求证:CE=AD;(2)、当AD=CF时,求证:H是AF的中点.15. 已知和都是等边三角形,分别连接 .
(1)、求证:CE=AD;(2)、当AD=CF时,求证:H是AF的中点.15. 已知和都是等边三角形,分别连接 . (1)、如图1,若 .
(1)、如图1,若 .①求的度数;
②延长交于点F , 求证:;
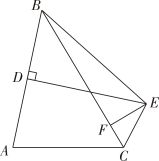
(2)、如图2,若点D在边上,延长交于点G , 连接 . 求证:平分 .16. 问题探究: (1)、如图1,中, , , 是高,求证:.(2)、如图2,在(1)条件下,、分别是和上的点,且 , 如果 , 那么四边形的面积是;(3)、如图3,四边形中,平分 , , , , 求的值.
(1)、如图1,中, , , 是高,求证:.(2)、如图2,在(1)条件下,、分别是和上的点,且 , 如果 , 那么四边形的面积是;(3)、如图3,四边形中,平分 , , , , 求的值.四、实践探究题
-
17. 数学活动课上,同学们用矩形纸片折叠作特殊的角.操作如下:
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:再一次折叠纸片,使折痕经过点 , 得到折痕BM,点的对应点为点 , 把纸片展平,连接MN,BN.
 (1)、如图1,当点N落在EF上,直接写出BM和MN的数量关系.(2)、如图2,当AB=BC时,延长MN交CD于点P.
(1)、如图1,当点N落在EF上,直接写出BM和MN的数量关系.(2)、如图2,当AB=BC时,延长MN交CD于点P.①求证:点P在∠NBC的平分线上;
②若AB=8cm,CP=3cm,求AM的长.