【提升版】浙教版数学八上2.7 探索勾股定理同步练习

试卷更新日期：2024-08-27 类型：同步测试

进入出卷网下载

一、选择题

1. 在Rt△ABC中，∠C＝90°，a＝12，b＝16，则c的长为（）

A、26 B、18 C、20 D、21

查看试题解析
2. 下列几组数中，不能作为直角三角形三边的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、7，24，25 C、4，5，6 D、 $\frac{3}{5}$ ， $\frac{4}{5}$ ，1

查看试题解析
3. 如图，在5×5的正方形网格中，从在格点上的点A ， B ， C ， D中任取三点，所构成的三角形恰好是直角三角形的个数为（）

A、3 B、2 C、1 D、0

查看试题解析
4. 如图，一棵大树在一次强台风中于离地面3m处折断倒下，树干顶部落在距根部4m处，这棵大树在折断前的高度为（）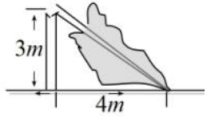

A、5米 B、7米 C、8米 D、12米

查看试题解析
5. 如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为5m，梯子的顶端B到地面的距离为12m，现将梯子的底端A向外移动到A'，使梯子的底端A'到墙根O的距离等于6m，同时梯子的顶端B下降至B'，那么BB'（　　　）

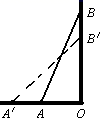A、小于1m B、大于1m C、等于1m D、小于或等于1m

查看试题解析
6. 《九章算术》中记录了这样一则“折竹抵地”问题：今有竹高一丈，末折抵地，去本四尺，问折者高几何？意思是：一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远（如图），则折断后的竹子高度为多少尺？（1丈=10尺）如果我们假设折断后的竹子高度为 $x$ 尺，根据题意，可列方程为（　　）

A、 $x^{2} + 4^{2} = 1 0^{2}$ B、 ${(10 - x)}^{2} + 4^{2} = 1 0^{2}$ C、 ${(10 - x)}^{2} + 4^{2} = x^{2}$ D、 $x^{2} + 4^{2} = {(10 - x)}^{2}$

查看试题解析
7.
图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中正方形顶点A、B在围成的正方体中的距离是（　　）

A、0 B、1 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，记四块阴影部分的面积分别为 $S_{1}^{}$ 、 $S_{2}^{}$ 、 $S_{3}^{}$ 、 $S_{4}^{}$ .若已知 $S_{Δ A B C}^{} = S$ ，则下列结论：① $S_{4}^{} = S$ ；② $S_{2}^{} = S$ ；③ $S_{1}^{} + S_{3}^{} = S_{2}^{}$ ；④ $S_{1}^{} + S_{2}^{} + S_{3}^{} + S_{4}^{} = 2.5 S$ ，
其中正确的结论是（）

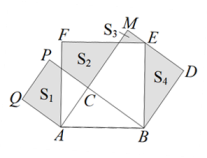A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

9. 直角三角形两直角边长分别为5和12，则它斜边上的高为．

查看试题解析
10. 如图，某自动感应门的正上方A处装着一个感应器，离地 $A B = 2.5$ 米，当人体进入感应器的感应范围内时，感应门就会自动打开.一个身高1.6米的学生 $C D$ 正对门，缓慢走到离门1.2米的地方时（ $B C = 1.2$ 米），感应门自动打开，则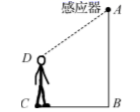 $A D =$ 米.

查看试题解析
11. 如图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，在 $R t △ A B C$ 中，若直角边 $A C = 6$ ， $B C = 5$ ，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长（图乙中的实线）是．

查看试题解析
12. 如图，阴影部分是两个正方形，其他三个图形是一个正方形和两个直角三角形，则阴影部分的面积之和为.

查看试题解析

三、解答题

13. 如图，在Rt△ABC中，∠C＝90°，AC＝8，AB＝10，AB的垂直平分线分别交AB、AC于点D、E.求AE的长.

查看试题解析
14. “儿童散学归来早，忙趁东风放纸鸢” $.$ 又到了放风筝的最佳时节．某校八年级 $(1)$ 班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作： $①$ 测得水平距离 $B D$ 的长为 $15$ 米； $②$ 根据手中剩余线的长度计算出风筝线 $B C$ 的长为 $25$ 米； $③$ 牵线放风筝的小明的身高为 $1.6$ 米．

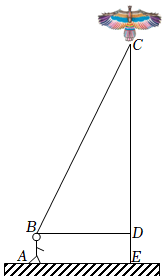(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降 $12$ 米，则他应该往回收线多少米？

查看试题解析
15. 如图正方形网格中的△ABC ，若小方格边长为1，请你根据所学的知识

(1)、求△ABC的面积；

(2)、判断△ABC是什么形状? 并说明理由.

查看试题解析
16. 如图，射线 $A M ⊥ A N$ 于点A、点C、B在 $A M$ 、 $A N$ 上，D为线段 $A C$ 的中点，且 $D E ⊥ B C$ 于点E.

(1)、若 $B C = 10$ ，直接写出 $A C^{2} + A B^{2}$ 的值；

(2)、若 $A C = 8$ ， $△ A B C$ 的周长为24，求 $△ A B C$ 的面积；

(3)、若 $A B = 6$ ，C点在射线 $A M$ 上移动，问此过程中， $B E^{2} - C E^{2}$ 的值是否为定值？若是，请求出这个定值；若不是，请求出它的取值范围.

查看试题解析
17. 如图，在 $△$ ABC中，∠ABC＝45°，CD⊥AB，BE⊥AC，垂足分别为D，E，F为BC中点，BE与DF、DC分别交于点G，H，∠ABE＝∠CBE．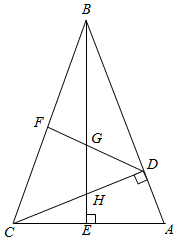

(1)、线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；

(2)、求证：BG²﹣GE²＝EA²；

(3)、若BC＝2 $\sqrt{2}$ ，求 $△$ BDH的面积．

查看试题解析

四、实践探究题

18. 为了测量学校旗杆的高度，八(1)班的两个数学研究小组设计了不同的方案，请结合下面表格的信息，完成任务问题．

测量旗杆的高度
测量工具	测量角度的仪器、皮尺等
测量小组	第一小组	第二小组
测量方案示意图
设计方案及测量数据	在地面确定点C，并测得旗杆顶端A的仰角，即∠ACB=45°．	如图1，绳子垂直挂下来时，相比旗杆，测量多出的绳子长度FP为2米．如图2，绳子斜拉直后至末端点P位置，测量点P到地面的距离PD为1米，以及点P到旗杆AB的距离PE为9米．

(1)、任务一：判断分析

第一小组要测旗杆AB的高度，只需要测量的长度为线段并说明理由．

(2)、任务二：推理计算

利用第二小组获得的数据，求旗杆的高度AB．

查看试题解析