【培优版】浙教版数学八上2.4 等腰三角形的判定定理同步练习

试卷更新日期：2024-08-26 类型：同步测试

进入出卷网下载

一、选择题

1. 在▱ $A B C D$ 中，用尺规作图作等腰 $△ A B E$ ，下列作图正确的是( )

A、 $① ②$ B、 $① ③$ C、 $③ ④$ D、 $② ④$

查看试题解析
2. 如图，在等边三角形 $A B C$ 中， $A D ⊥ B C$ ，在 $A B$ ， $C B$ 上分别取点M ， N ，且 $A M = B N = 8$ ， $D N = 4$ ，在 $A D$ 上有一动点 $P$ ，则 $P M + P N$ 的最小值为（　　）

A、12 B、14 C、16 D、18

查看试题解析
3. 有一道题目：“在△ABC中，AB＝AC ， ∠A＝40°，分别以B、C为圆心，以BC长为半径的两条弧相交于D点，求∠ABD的度数”．嘉嘉的求解结果是∠ABD＝10°．淇淇说：“嘉嘉考虑的不周全，∠ABD还应有另一个不同的值．”下列判断正确的是（）

A、淇淇说得对，且∠ABD的另一个值是130° B、淇淇说的不对，∠ABD就得10° C、嘉嘉求的结果不对，∠ABD应得20° D、两人都不对，∠ABD应有3个不同值

查看试题解析
4. 如图：点 $C$ 在 $A B$ 上， $△ D A C$ 、 $△ E B C$ 均是等边三角形， $A E$ 、 $B D$ 分别与 $C D$ 、 $C E$ 交于点 $M$ ， $N$ ，则下列结论 $① A E = D B$ ， $② C M = C N$ ， $③ △ C M N$ 为等边三角形， $④ M N / / B C .$ 正确的有个．（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 如图，等边 $△ A B C$ 中，D为AC中点，点P、Q分别为AB、AD上的点， $B P = A Q = 4$ ， $Q D = 3$ ，在BD上有一动点E，则 $P E + Q E$ 的最小值为（）

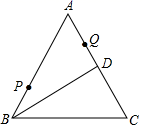A、7 B、8 C、10 D、12

查看试题解析
6. 如图，C为线段AE上一动点（不与点A ， E重合），在AE同侧分别作等边△ABC和等边△ECD ， AD与BE交于点O ， AD与BC交于点P ， BE与CD交于点Q连接PQ ．以下五个结论正确的是（）
① $A D = B E$ ；②PQ∥AE； ③ $A P = B Q$ ；④ $D E = D P$ ；⑤ $∠ A O B = 6 0^{∘}$

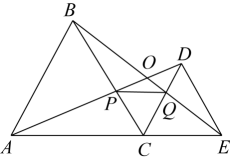A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤

查看试题解析
7. 如图，已知 $∠ A O B = 120 °$ ，点 $D$ 是 $∠ A O B$ 的平分线上的一上定点，点 $E$ ， $F$ 分别在射线 $O A$ 和射线 $O B$ 上，且 $∠ E D F = 60 °$ .下列结论：① $△ D E F$ 是等边三角形；②四边形 $D E O F$ 的面积是一个定值；①当 $D E ⊥ O A$ 时， $△ D E F$ 的周长最小；④当 $D E ∥ O B$ 时， $D F$ 也平行于 $O A$ .其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在等腰 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ， $A D ⊥ B C$ 于点D，点P是 $C A$ 延长线上一点，点O在 $A D$ 延长线上， $O P = O B$ ，下面的结论：① $∠ A P O - ∠ O B D = 30 °$ ；② $△ B P O$ 是正三角形；③ $A B - A P = A O$ ；④ $S_{四边形 A O B P} = 2 S_{△ B O C}$ ，其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 由于木质衣架没有柔性，所以在挂置衣服的时候不太方便操作.小敏设计了一种衣架，在使用时能轻易收拢，套进衣服后松开即可.如图①所示，衣架杆OA=OB=18 cm.若衣架收拢时，∠AOB=60°，如图②所示，则此时A，B两点之间的距离是cm.

查看试题解析
10. 如图， $△ A B C$ 中， $∠ C = 2 ∠ B A C$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D ，过点A作 $A E ⊥ B D$ 交 $B D$ 的延长线于点E ．若 $A B = 18 c m$ ， $△ B D C$ 的周长为 $24 c m$ ， $△ A B D$ 的面积为 $12 c m^{2}$ ，则 $A E =$ $c m$ ．

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $B C = 6$ ， D为 $A B$ 的中点，P为 $B C$ 上一动点，连接 $A P$ ， $D P$ ，则 $A P + D P$ 的最小值是.

查看试题解析
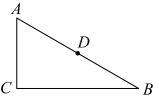12. 如图，AB＝BE ， ∠DBC＝ $\frac{1}{2}$ ∠ABE ， BD⊥AC ，则下列结论正确的是：．（填序号）
①BC平分∠DCE；②∠ABE+∠ECD＝180°；③AC＝2BE+CE；④AC＝2CD-CE ．

查看试题解析

三、作图题

13. 如图，在 $6 \times 6$ 的正方形网格中，每个小正方形的顶点称为格点， $△ A B C$ 的顶点均在格点上．按要求完成下列画图．（要求：用无刻度直尺，保留必要的画图痕迹，不写画法）

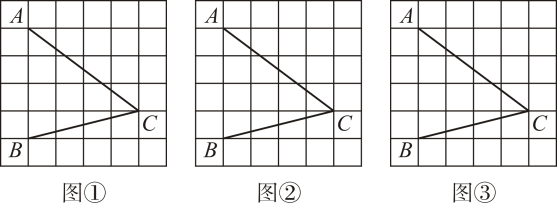(1)、在图①中画出一个 $△ A B D$ ，使 $S_{△ A B D} = S_{△ A B C}$ ， D为格点（点D不在点C处）：

(2)、在图②中的边BC上找一点E ，连接AE ，使 $A E ⊥ B C$ ；

(3)、在图③中的边BC上找一点F ，使点F到AB和AC所在直线的距离相等．

查看试题解析

四、解答题

14.

(1)、如图1，点 $D$ 、 $E$ 分别是等边 $△ A B C$ 边 $A C$ 、 $A B$ 上的点，连接 $B D$ 、 $C E$ ，若 $A E = C D$ ，求证： $B D = C E$

(2)、如图2，在（1）问的条件下，点 $H$ 在 $B A$ 的延长线上，连接 $C H$ 交 $B D$ 延长线于点 $F$ ，．若 $B F = B C$ ，求证： $E H = E C$ ．

查看试题解析
15. 在学习七下课本121页“三线合一”时罗老师在课堂上进行了探究式教学．


(1)、【问题原型】定理：等腰三角形顶角的角平分线、底边上的中线、底边上的高重合．如图，在 $△ A B C$ 中， $A B = A C ， A D$ 平分 $∠ B A C$ ．根据图形1用几何语言写出该定理
①∵ $A B = A C$ ， $A D$ 平分 $∠ B A C$ ，
∴                                  ，                             ；
②在 $△ A B C$ 中， $A B = A C ， A D ⊥ B C ， △ A B C$ 的周长为32， $△ A B D$ 的周长为23，则 $A D$ 的长为                ．


(2)、【问题提出】罗老师提出：当三角形的一条角平分线恰好也是这个三角形的中线时，这个三角形是等腰三角形吗？经过小组合作探究后罗老师发现了同学们有以下两种解题思路，请任选其中一种，完成命题的证明．
已知：在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ，且点D是 $B C$ 的中点．求证： $A B = A C$ ．
方法一：如图2，延长 $A D$ 到点E，使 $A D = D E$ ，连接 $C E$ ．
方法二：如图3，过点D分别作 $A B ， A C$ 的垂线，垂足分别为E，F．

(3)、【拓展延伸】如图4，在 $△ A B C$ 中， $B C = 12 ， A D$ 平分 $∠ B A C$ ，点E为 $A C$ 中点， $A D$ 与 $B E$ 相交于点F，过点B作 $B H ⊥ A D$ 交 $A D$ 延长线于点H，设 $△ B F H ， △ A E F$ 的面积分别为 $S_{1} ， S_{2}$ ，若 $A B - A C = 4$ ，试求 $S_{1} - S_{2}$ 的最大值．

查看试题解析

五、实践探究题

16. 阅读与思考：分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式，比如：四项的多项式一般按照“两两”分组或“三一”分组，进行分组分解.
例1：“两两分组”： $a x + a y + b x + b y$
解：原式 $= (a x + a y) + (b x + b y)$
$= a (x + y) + b (x + y)$
$= (a + b) (x + y)$
例2：“三一分组”： $2 x y + x^{2} - 1 + y^{2}$
解：原式 $= (x^{2} + 2 x y + y^{2}) - 1$
$= {(x + y)}^{2} - 1$
$= (x + y + 1) (x + y - 1)$
归纳总结：用分组分解法分解因式要先恰当分组，然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下，解答下列问题：

(1)、分解因式：
① $x^{2} - x y + 4 x - 4 y$ ；
② $x^{2} - y^{2} + 4 y - 4$ .

(2)、已知 $△ A B C$ 的三边a ， b ， c满足 $a^{2} - a c - b^{2} + b c = 0$ ，试判断 $△ A B C$ 的形状.

查看试题解析
17. 已知在 $△ A B C$ 中， $A B = A C$ ，过点 $B$ 引一条射线 $B M$ ， $D$ 是 $B M$ 上一点．

(1)、【问题解决】
如图1，若 $∠ A B C = 60 °$ ，射线 $B M$ 在 $∠ A B C$ 内郃， $∠ A D B = 60 °$ ，求证： $∠ B D C = 60 °$ ，小明的做法是：在 $B M$ 上取一点 $E$ ，使得 $A E = A D$ ，再通过已知条件，求得 $∠ B D C$ 的度数．请你帮助小明写出证明过程：

(2)、【类比探究】
如图2，已知 $∠ A B C = ∠ A D B = 30 °$ ，当射线 $B M$ 在 $∠ A B C$ 内，求 $∠ B D C$ 的度数．

(3)、【变式迁移】
如图3，已知 $∠ A B C = ∠ A D B = 30 °$ ，当射线 $B M$ 在 $B C$ 下方， $∠ B D C$ 的度数会变化时？若改变，请求出 $∠ B D C$ 的度数，若不变，请说明理由．

查看试题解析

六、综合题

18. 概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.

从三角形 $($ 不是等腰三角形 $)$ 一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.

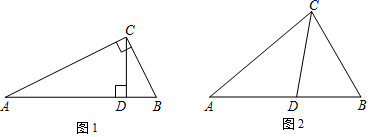(1)、理解概念
如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，请写出图中两对“等角三角形”

(2)、概念应用
如图2，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40 °$ ， $∠ B = 60 °$ .
求证： $C D$ 为 $△ A B C$ 的等角分割线.

(3)、在 $△ A B C$ 中， $∠ A = 42 °$ ， $C D$ 是 $△ A B C$ 的等角分割线，直接写出 $∠ A C B$ 的度数.

查看试题解析
19. 在等边三角形 $A B C$ 中，D为射线 $C B$ 上一点，连接 $A D$ ，点B关于直线 $A D$ 的对称点为E，连接 $A E ， D E ， C E$ ．

(1)、如图1，点D在线段 $B C$ 上， $∠ B A D = 15 °$ ，求 $∠ B C E$ 的度数；

(2)、射线 $A D$ 与射线 $C E$ 的交于点F，过点D作 $D G ∥ A C$ 交射线 $A B$ 于点G，连接 $G E$ 交 $A D$ 于点H．
①如图2，点D在线段 $B C$ 上，求证： $△ A G H ≅ △ C D F$ ；
②点D在线段 $C B$ 延长线上，用等式表示线段 $A H ， F H$ 和 $C E$ 之间的数量关系，并说明理由．

查看试题解析