【培优版】浙教版数学八上2.3 等腰三角形的性质定理同步练习

试卷更新日期：2024-08-26 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在已知的 $△ A B C$ 中，按以下步骤作图： $①$ 分别以点 $B$ 和点 $C$ 为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于点 $M$ ， $N$ ； $②$ 作直线 $M N$ 交 $A B$ 于点 $D$ ，连接 $C D .$ 若点 $D$ 是 $A B$ 的中点，则 $∠ A C B$ 的度数是( )

A、 $90 °$
B、 $95 °$
C、 $100 °$
D、 $105 °$

查看试题解析
2. 如图，分别是小明、小颖和小亮三位同学用尺规作 $∠ A O B$ 的平分线的图示，对于三人不同的作法，其中正确的个数是（）

A、0个 B、1 个 C、2个 D、3个

查看试题解析
3. 在凸五边形ABCDE中， $A B = A E$ ， $B C = D E$ ， F是CD的中点．下列条件中，不能推出AF与CD一定垂直的是（）

A、 $∠ A B C = ∠ A E D$ B、 $∠ B A F = ∠ E A F$ C、 $∠ B C F = ∠ E D F$ D、 $∠ A B D = ∠ A E C$

查看试题解析
4. 如图， $△ A B C$ 是等边三角形， $A D$ 是 $B C$ 边上的高，点 $E$ 是 $A C$ 边的中点，点 $P$ 是线段 $A D$ 上的一个动点，当 $P C + P E$ 最小时， $∠ C E P$ 为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
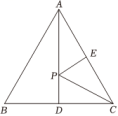5. △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）

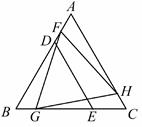A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长

查看试题解析
6. 如图，在 $△ A B C$ 中， $A D ， B E$ 分别为 $B C ， A C$ 边上的高， $A D ， B E$ 相交于点 $F ， A D = B D$ ，连接 $C F$ ，则下列结论：① $B F = A C$ ；② $∠ F C D = ∠ D A C$ ；③ $C F ⊥ A B$ ；④若 $B F = 2 E C$ ，则 $△ F D C$ 周长等于 $A B$ 的长．其中正确的有（）

A、①② B、①③ C、①③④ D、②③④

查看试题解析

二、填空题

7. 如图，在 $△ A B C$ 中， $∠ D C E = 40 °$ ， $A E = A C$ ， $B C = B D$ ，则 $∠ A C B$ 的度数为

查看试题解析
8. 如图，在△ABC中，∠B=70°，∠C=25°，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 的长为半径面筑两弧相交于点M、N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为.

查看试题解析
9. 如图，已知 $A B = A_{1} B, A_{1} C = A_{1} A_{2}, A_{2} D = A_{2} A_{3}, A_{3} E = A_{3} A_{4}, ∠ B = 20 °$ ，则 $∠ A_{4}$ 的度数为．

查看试题解析
10. 如图，边长为2的等边 $△ A B C$ 中， $A D$ 是边 $B C$ 上的中线，点E在 $A D$ 上，连接 $C E$ ，在 $A C$ 的下方作等边 $△ C E F$ ，连接 $D F$ ，则 $△ C D F$ 周长的最小值是．

查看试题解析

三、解答题

11. 已知：AD为△ABC的中线，分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF ，且AE＝AB ， AF＝AC ，连接EF ， ∠EAF+∠BAC＝180°．

(1)、如图1，若∠ABE＝65°，∠ACF＝75°，求∠BAC的度数．

(2)、如图1，求证：EF＝2AD ．

(3)、如图2，设EF交AB于点G ，交AC于点R ， FC与EB交于点M ，若点G为EF中点，且∠BAE＝60°，请探究∠GAF和∠CAF的数量关系，并证明你的结论．

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线交 $A B$ 于 $N$ ，交 $A C$ 于 $M$ ．

(1)、若 $∠ A B C = 65 °$ ，求 $∠ N M A$ 的度数．

(2)、连接 $M B$ ，若 $A C = 12 c m$ ， $B C = 8 c m$ ．
①求 $△ M B C$ 的周长；
②在直线 $M N$ 上是否有在点 $P$ ，使 $P B + C P$ 的值最小，若存在，标出点 $P$ 的位置并求 $P B + C P$ 的最小值，若不存在，说明理由．

查看试题解析
13. 如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．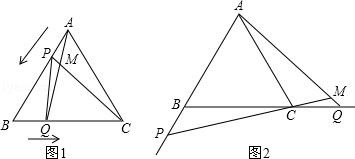

(1)、求证：△ABQ≌△CAP；

(2)、当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．

(3)、如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．

查看试题解析
14. 如图， $△ A B C$ 是等边三角形，点 $D$ 在 $A C$ 上，点 $E$ 在 $B C$ 的延长线上，且 $B D = D E$ ．

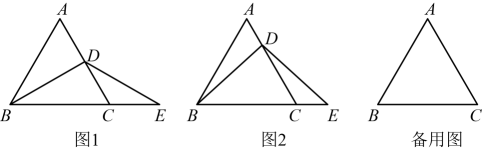(1)、若点 $D$ 是 $A C$ 的中点，如图1，则线段 $A D$ 与 $C E$ 的数量关系是；

(2)、若点 $D$ 不是 $A C$ 的中点，如图2，试判断 $A D$ 与 $C E$ 的数量关系，并证明你的结论；(提示：过点 $D$ 作 $D F ∥ B C$ ，交 $A B$ 于点 $F$ )

(3)、若点 $D$ 在线段 $A C$ 的延长线上，（2）中的结论是否仍成立？如果成立，请给予证明；如果不成立，请说明理由．

查看试题解析

四、实践探究题

15. 已知 $△ A B C$ 和 $△ D E F$ 均为等边三角形，点 $D$ 在 $△ A B C$ 的边 $A B$ 上，点 $F$ 在直线 $A C$ 上．

(1)、若点 $C$ 和点 $F$ 重合（如图①），求证： $A E ∥ B C$ ．

(2)、若点 $F$ 在 $A C$ 的延长线上（如图②），（1）中的结论还能成立吗？给出你的结论并证明．

查看试题解析
16. 【教材呈现】以下是人教版八年级上册数学教材第53页的部分内容．
如图1，四边形 $A B C D$ 中， $A D = C D$ ， $A B = C B$ ．我们把这种两组邻边分别相等的四边形叫做“筝形”

(1)、【性质探究】如图1，连接筝形ABCD的对角线AC、BD交于点O，试探究筝形ABCD的性质，并填空：对角线AC、BD的关系是：；图中∠ADB、∠CDB的大小关系是： .

(2)、【概念理解】如图2，在△ABC中，AD⊥BC，垂足为 $D$ ， △EAB与△DAB关于 $A B$ 所在的直线对称，△FAC与 $△ D A C$ 关于 $A C$ 所在的直线对称，延长 $E B$ ， $F C$ 相交于点 $G$ ．请写出图中所有的“筝形”，并选择其中一个进行证明；

(3)、【应用拓展】如图3，在（2）的条件下，连接 $E F$ ，分别交 $A B$ 、 $A C$ 于点 $M$ 、 $H$ ．求证：∠BAC=∠FEG.

查看试题解析