【提升版】浙教版数学八上2.3 等腰三角形的性质定理同步练习
试卷更新日期:2024-08-26 类型:同步测试
一、选择题
-
1. 如图,在中, , 为的平分线,若 , 则的长为( )
 A、2 B、3 C、4 D、52. 如图,直线l∥m,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若∠ABE=21°,则∠ACD的度数是( )
A、2 B、3 C、4 D、52. 如图,直线l∥m,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若∠ABE=21°,则∠ACD的度数是( ) A、 B、 C、 D、3. 如图,直线 .以直线 上的点A为圆心、适当长为半径画弧,分别交直线 于点B、C,连结 .若 ,则 的度数为( )
A、 B、 C、 D、3. 如图,直线 .以直线 上的点A为圆心、适当长为半径画弧,分别交直线 于点B、C,连结 .若 ,则 的度数为( ) A、 B、 C、 D、4. 如图,已知 , 是内部的一点,且 , 点、分别是、上的动点,若周长的最小值等于 , 则( )
A、 B、 C、 D、4. 如图,已知 , 是内部的一点,且 , 点、分别是、上的动点,若周长的最小值等于 , 则( ) A、
A、
B、
C、
D、5. 如图,在中,以点为圆心,AC长为半径作弧,交BC于点;再分别以点B,D为圆心,大于的长为半径作弧,两弧分别交于点M,N,连接MN,交AB于点.已知的周长为 , 则AB的长为( ) A、7 B、8 C、9 D、106. 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案,如图.其中与都是等腰三角形,且它们关于直线对称,点分别是底边的中点, . 下列推断错误的是( )
A、7 B、8 C、9 D、106. 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案,如图.其中与都是等腰三角形,且它们关于直线对称,点分别是底边的中点, . 下列推断错误的是( ) A、 B、 C、 D、7. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,等于( )
A、 B、 C、 D、7. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,等于( )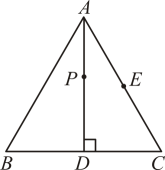 A、 B、 C、 D、8. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( )
A、 B、 C、 D、8. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
9. 在 中, , 点 在 边上,连接 , 若 为直角三角形,则 的度数是.10. 定义: 等腰三角形的底边长与其腰长的比值 称为这个等腰三角形的"优美比"。若等腰三角形的周长为 13 cm ,一边长为 5 cm , 则它的"优美比" 为11. 如图,在中, , , 的平分线与的垂直平分线交于点 , 将沿点在上,点在上折叠,点与点恰好重合,已知 , 则的度数为
 12. 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=6,点F是线段AD上的动点,则BF+EF的最小值为 .
12. 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=6,点F是线段AD上的动点,则BF+EF的最小值为 .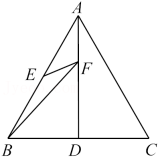
三、解答题
-
13. 如 图, 是 的高线, 的垂直平分线分别交 于点 .
 (1)、 若 , 求 的度数;(2)、 试说明: .14. 如图在中、 , 分别垂直平分边和边 , 交边于、两点、与所在直线相交于点 .
(1)、 若 , 求 的度数;(2)、 试说明: .14. 如图在中、 , 分别垂直平分边和边 , 交边于、两点、与所在直线相交于点 . (1)、若、求的周长;(2)、若 , 求的度数.
(1)、若、求的周长;(2)、若 , 求的度数.四、综合题

