浙教版（2024）数学七年级上册《第3章实数》单元提升测试卷

试卷更新日期：2024-08-25 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 计算 $\sqrt{9^{2} - 6^{2}}$ 所得结果是（）

A、3 B、 $\sqrt{6}$ C、 $3 \sqrt{5}$ D、 $\pm 3 \sqrt{5}$

查看试题解析
2. 十六世纪，意大利数学家塔尔塔利亚把大正方形分割成11个小正方形．若图中所给的三个小正方形的面积分别为4，9和16，则这个大正方形的边长为（）

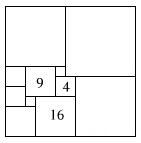A、11 B、12 C、13 D、14

查看试题解析
3. 已知 $8.6 2^{2} = 74.3044$ ，若 $x^{2} = 0.743044$ ，则 $x$ 的值（）

A、86.2 B、 $0.862$ C、 $\pm 0.862$ D、 $\pm 86.2$

查看试题解析
4. 若 $a^{2} = 4 ， | b | = 5$ ，且 $a b < 0$ ，则 $a + b$ 的值是（）

A、3 B、 $- 3$ C、3或 $- 3$ D、 $- 3$ 或 $- 7$

查看试题解析
5. 若 $\sqrt{5} ＜$ m $＜ \sqrt{10}$ ，则整数m的值为（）

A、2 B、3 C、4 D、5

查看试题解析
6. 下列说法：①有理数与数轴上的点一一对应；②1的平方根是它本身；③立方根是它本身的数是0，1；④对于任意一个实数 $a$ ，都可以用 $\frac{1}{a}$ 表示它的倒数．⑤任何无理数都是无限不循环小数.正确的有（）个.

A、0 B、1 C、2 D、3

查看试题解析
7. 下列说法中正确的是（　　　）

A、 $81$ 的平方根是 $9$ B、 $\sqrt{16}$ 的算术平方根是 $4$ C、 $\sqrt[3]{- a}$ 与 $- \sqrt[3]{a}$ 相等 D、 $64$ 的立方根是 $\pm 4$

查看试题解析
8. 下列各组数中，互为相反数的是（）

A、 $- \sqrt{9}$ 与 $\sqrt[3]{27}$ B、 $\sqrt[3]{- 8}$ 与 $- \sqrt[3]{8}$ C、 $| - \sqrt{2} |$ 与 $\sqrt{2}$ D、 $\sqrt{2}$ 与 $\sqrt[3]{- 8}$

查看试题解析
9. 实数a在数轴上的对应位置如图所示，则 $\sqrt{a^{2}} + 1 + | a - 1 |$ 的化简结果是（）

A、1 B、2 C、2a D、1﹣2a

查看试题解析
10. 按如图所示的程序计算，若开始输入的n值为 $\sqrt{2}$ ，则最后输出的结果是（）

A、14 B、16 C、8+5 $\sqrt{2}$ D、14+ $\sqrt{2}$

查看试题解析

二、填空题（每题3分，共18分）

11. $\sqrt{64}$ 的立方根是．

查看试题解析
12. 若实数 $a$ 、 $b$ 满足 $\sqrt{a - 2} + | b + 4 | = 0$ ，则 $a b =$ .

查看试题解析
13. $\sqrt{16}$ 的平方根等于.

查看试题解析
14. 有一个数值转换器，原理如下：当输入的 $x$ 为 $64$ 时，输出的 $y$ 的值．

查看试题解析
15. 定义 $[x]$ 为不大于x的最大整数，如 $[2] = 2$ ， $[\sqrt{3}] = 1$ ， $[4.1] = 4$ ，则满足 $[\sqrt{n}] = 5$ ，则 $n$ 的最大整数为.

查看试题解析
16. 已知|x|=5，y²=1，且 $\frac{x}{y}$ ＞0，则x﹣y= ．

查看试题解析

三、解答题（共9题，共72分）

17. 计算： $\sqrt{16} - \sqrt{(- 3)^{2}} + | \sqrt{3} - 2 |$ ．

查看试题解析
18. 计算： $| \sqrt{3} - 2 | - \sqrt{3^{2}} + {(- 2)}^{2} - \sqrt[3]{8}$ ．

查看试题解析
19. 计算：
$- 2^{2} \times 2 + \sqrt{36} \times (\frac{1}{3} - \frac{1}{2}) - \sqrt[3]{27} \div (- 1 \frac{1}{2})$

查看试题解析
20. 计算： $\sqrt{24} \div \sqrt{3} + | 3 - \sqrt{8} | - \sqrt{25}$ .

查看试题解析
21. 已知 $4 a - 11$ 的平方根是 $\pm 5$ ， $2 a + b - 1$ 的算术平方根是1， $c$ 是 $\sqrt{50}$ 的整数部分．

(1)、求 $a$ ， $b$ ， $c$ 的值；

(2)、求 $a + c - 3 b$ 的立方根．

查看试题解析
22. 阅读理解.
$∵ \sqrt{4} < \sqrt{5} < \sqrt{9}$ 即 $2 < \sqrt{5} < 3$

$∴ 1 < \sqrt{5} - 1 < 2$

$∴ \sqrt{5} - 1$ 的整数部分为1，

$∴ \sqrt{5} - 1$ 的小数部分为 $\sqrt{5} - 2$

解决问题：已知a是 $\sqrt{17}$ ﹣3的整数部分，b是 $\sqrt{17}$ ﹣3的小数部分.

(1)、求a，b的值；

(2)、求（﹣a）³+（b+4）²的平方根，提示：（ $\sqrt{17}$ ）²＝17.

查看试题解析
23. 对于含算术平方根的算式，在有些情况下，可以不需要计算出结果也能将算术平方根符号去掉，例如： $\sqrt{{(1 - \frac{1}{2})}^{2}} = \sqrt{{(\frac{1}{2})}^{2}} = \frac{1}{2}$ =1- $\frac{1}{2}$
$\sqrt{{(\frac{1}{2} - 1)}^{2}} = \sqrt{{(- \frac{1}{2})}^{2}} = 1 - \frac{1}{2}$
观察上述式子的特征，解答下列问题：

(1)、把下列各式写成去掉算术平方根符号的形式(不用写出计算结果)：
$\sqrt{（ 10 - 6 ）^{2}}$ =；
$\sqrt{（ 7 - 9 ）^{2}}$ =.

(2)、当a>b时 $\sqrt{（ a - b ）^{2}}$ = ，当a<b时， $\sqrt{（ a - b ）^{2}}$ =

(3)、计算： $\sqrt{（ \frac{1}{3} - \frac{1}{2} ）^{2}} + \sqrt{(\frac{1}{4} - \frac{1}{3})^{2}} + \sqrt{(\frac{1}{5} - \frac{1}{4})^{2}} + . . . + \sqrt{(\frac{1}{2023} - \frac{1}{2022})^{2}}$

查看试题解析
24. 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、 $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确；
信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5﹣2得来的；
信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如2＜ $\sqrt{5}$ ＜3，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ；
根据上述信息，回答下列问题：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是；

(2)、8+ $\sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为a＜8+ $\sqrt{3}$ ＜b则a+b＝；

(3)、若 $\sqrt{39}$ －2＝a+b，其中a是整数，且0＜b＜1，请求2a-b的相反数．

查看试题解析
25. 教材上有这样一个合作学习活动：如图1，依次连结2×2方格四条边的中点A ， B ， C ， D ，得到一个阴影正方形．设每一小方格的边长为1，得到阴影正方形面积为2．

(1)、【基础尝试】：
发现图1这个阴影正方形的边长就是小方格的对角线长，则小方格对角线长是，由此我们得到一种在数轴上找到无理数的方法；

(2)、【画图探究】：
如图2，以1个单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于M ， N两点，则点M表示的数为；

(3)、【问题解决】：
如图3，3×3网格是由9个边长为1的小方格组成．
①画出面积是5的正方形，使它的顶点在网络的格点上；
②请借鉴（2）中的方法在数轴上找到表示实数 $\sqrt{5} - 1$ 的准确位置．（保留作图痕迹并标出必要线段长）

查看试题解析

浙教版（2024）数学七年级上册《第3章 实数》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

浙教版（2024）数学七年级上册《第3章实数》单元提升测试卷