人教版九年级上学期数学课时进阶测试23.1图形的旋转(三阶)
试卷更新日期:2024-08-25 类型:同步测试
一、选择题(每题3分)
-
1. 如图,∠MAN=60°,点B、C分别在AM、AN上,AB=AC , 点D在∠MAN内部、△ABC外部,连接BD、CD、AD . 下列结论:①DB+DC≥DA;②S△BDC≤BD•DC;③若DB=m , DC=n , 则S△ADB≤+mn . 其中错误的结论个数为( )个.
 A、0 B、1 C、2 D、32. 如图,正方形的顶点、在上,顶点、在内,将正方形绕点顺时针旋转 , 使点落在上.若正方形的边长和的半径相等,则旋转角度等于( )
A、0 B、1 C、2 D、32. 如图,正方形的顶点、在上,顶点、在内,将正方形绕点顺时针旋转 , 使点落在上.若正方形的边长和的半径相等,则旋转角度等于( ) A、 B、 C、 D、3. 如图,将边长为的正方形ABCD绕点B逆时针旋转30°得到正方形A′BC′D′,AD与C′D′交于点M , 那么图中点M的坐标为( )
A、 B、 C、 D、3. 如图,将边长为的正方形ABCD绕点B逆时针旋转30°得到正方形A′BC′D′,AD与C′D′交于点M , 那么图中点M的坐标为( ) A、 B、 C、 D、4. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )
A、 B、 C、 D、4. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )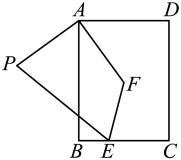 A、 B、 C、4 D、5. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )
A、 B、 C、4 D、5. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )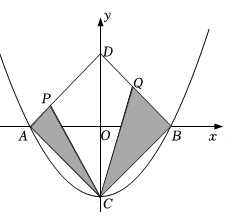 A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小6. 如图所示,边长为2的正三角形ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转30°得到三角形OA1B1 , 则点A1的坐标为( )
A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小6. 如图所示,边长为2的正三角形ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转30°得到三角形OA1B1 , 则点A1的坐标为( ) A、( ,1) B、( ,-1) C、(-1, ) D、(2,1)
A、( ,1) B、( ,-1) C、(-1, ) D、(2,1)二、填空题(每题3分)
-
7. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=
 8. 如图,点A , C分别是y轴,x轴正半轴上的动点, , 将线段绕点A顺时针旋转60°得到线段 , 则的最小值是 .
8. 如图,点A , C分别是y轴,x轴正半轴上的动点, , 将线段绕点A顺时针旋转60°得到线段 , 则的最小值是 . 9. 如图,在△ABC中,∠ACB=90°,AC=8,将△ABC绕点C按逆时针方向旋转得到△A1B1C,满足A1B1∥AC,过点B作BE⊥A1C,垂足为E,连接AE,若S△ABE=3S△ACE , 则AB的长为 .
9. 如图,在△ABC中,∠ACB=90°,AC=8,将△ABC绕点C按逆时针方向旋转得到△A1B1C,满足A1B1∥AC,过点B作BE⊥A1C,垂足为E,连接AE,若S△ABE=3S△ACE , 则AB的长为 . 10. 在平面直角坐标系中, 为原点,点 在第一象限, , , ,把 绕点 顺时针旋转60°得到 ,点 , 的对应点分别为 , ,则 的值为 .11. 如图,在正方形中,点是上一动点,点是的中点,绕点顺时针旋转得到 , 连接 , 给出结论:;;③若正方形的边长为2,则点在射线上运动时,有最小值其中结论正确的是 .
10. 在平面直角坐标系中, 为原点,点 在第一象限, , , ,把 绕点 顺时针旋转60°得到 ,点 , 的对应点分别为 , ,则 的值为 .11. 如图,在正方形中,点是上一动点,点是的中点,绕点顺时针旋转得到 , 连接 , 给出结论:;;③若正方形的边长为2,则点在射线上运动时,有最小值其中结论正确的是 .
三、作图题
-
12. 如图,方格纸中的每个小正方形的边长都是 , 小正方形的顶点称作格点,的三个顶点都在格点上,把先向右平移个单位,再向下平移个单位得 , 再将绕点顺时针旋转得结合所给的平面直角坐标系,回答下列问题:
 (1)、在平面直角坐标系中画出和;(2)、图中的能不能通过顺时针旋转得到?如果可以,请写出旋转中心的坐标及旋转角的度数;如果不能,说明理由.
(1)、在平面直角坐标系中画出和;(2)、图中的能不能通过顺时针旋转得到?如果可以,请写出旋转中心的坐标及旋转角的度数;如果不能,说明理由.四、解答题
-
13. 如图1,在正方形ABCD内作 , AE交BC于点E,AF交CD于点F,连接EF,过点A作 , 垂足为H.
图1
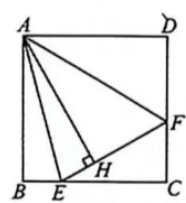 图2
图2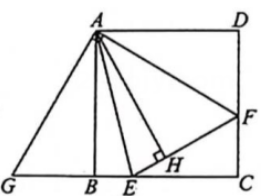 图3
图3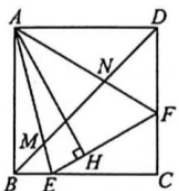 (1)、如图2,将绕点A顺时针旋转得到.
(1)、如图2,将绕点A顺时针旋转得到.①求证:.
②若 , , 求AH的长.
(2)、如图3,连接BD交AE于点M,交AF与点N,请探究并猜想:线段BM,MN,ND之间有什么关系?请说明理由?
-