广东省韶关乐昌市2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2024-08-19 类型：期中考试

进入出卷网下载

一、选择题（本题共计10小题，每题3分，共计30分．）

1. 龙华区正推行垃圾分类政策，下列垃圾分类标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，关于x的一元二次方程的是（）

A、 $x + 2 x = 1$ B、 $x^{2} + 2 y = 2$ C、 $2 x - x^{2} = 3$ D、 $x + \frac{1}{y} = 4$

查看试题解析
3. 关于二次函数 $y = (x + 2)^{2} - 3$ ，下列说法正确的是（）

A、抛物线开口向上 B、抛物线的对称轴是 $x = 2$ C、当 $x = - 2$ 时，有最大值 $- 3$ D、抛物线的顶点坐标是 $(2, - 3)$

查看试题解析
4. 方程3 $x^{2}$ -4=-2x的二次项系数、一次项系数、常数项分别为（）

A、3，-4，-2 B、3，2，-4 C、3，-2，-4 D、2，-2，0

查看试题解析
5. 抛物线y＝x²﹣mx﹣m²+1的图象过原点，则m为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
6. 一元二次方程 $x^{2} - 7 x - 2 = 0$ 的实数根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
7. 如图，将 $△ A B C$ 绕点A旋转后得到 $△ A D E$ ，则旋转方式是（）

A、顺时针旋转 $90 °$ B、逆时针旋转 $45 °$ C、顺时针旋转 $45 °$ D、逆时针旋转 $90 °$

查看试题解析
8. 根据下列表格的对应值，判断方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ， a ， b ， c为常数）一个解的范围是（）
x
3.23
3.24
3.25
3.26
$a x^{2} + b x + c$
$\begin{array}{l} - 0.06 \end{array}$
$\begin{array}{l} - 0.02 \end{array}$
0.03
0.07

A、 $3 < x < 3.23$ B、 $3.23 < x < 3.24$ C、 $3.24 < x < 3.25$ D、 $3.25 < x < 3.26$

查看试题解析
9. 抛物线y=-3(x+1)²不经过的象限是（）

A、第一、二象限 B、第二、四象限 C、第三、四象限 D、第二、三象限

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列结论：① $a b c > 0$ ；② $9 a + c > 0$ ；③ $a x^{2} + b x + c = 0$ 的两个根是 $x_{1} = - 2 ， x_{2} = 4$ ；④ $b ： c = 1 ： 4$ 其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本题共计5小题，每题3分，共计15分．）

11. 方程3x²+6x＝0的解是.

查看试题解析
12. 若点（m，3）与点（2，n）关于原点对称，则m+n＝．

查看试题解析
13. 已知二次函数 $y = x^{2} - x - 1$ 的图象与 $x$ 轴的一个交点为 $(m, 0)$ ，则代数式 $m^{2} - m + 2015$ 的值为．

查看试题解析
14. 若关于x的一元二次方程x²﹣mx+6＝0的一个根为2，则它的另一个根为．

查看试题解析
15. 如图，将 $R t △ A B C$ 绕直角顶点C顺时针旋转 $90 °$ ，得 $△ A^{'} B^{'} C$ ，连接 $A B^{'}$ ，若 $∠ A^{'} B^{'} A = 25 °$ ，则 $∠ B$ 的大小为．

查看试题解析

三、解答题（本题共计8小题，共计75分．）

16. 解一元二次方程： $x^{2} - 2 x - 15 = 0$ ．

查看试题解析
17. 某地2016年为做好“精准扶贫投资”，投入资金20万元用于异地安置，并规划投入资金逐年增加，2018年投入资金 $28.8$ 万元．求2016年到2018这两年的平均增长率为多少？

查看试题解析
18. 在平面直角坐标系中 $x O y$ 中，抛物线 $y = a x^{2} - 4 a x + 1$ ．

(1)、求抛物线的对称轴；

(2)、若抛物线过点 $A (- 1, 6)$ ，求二次函数的表达式．

查看试题解析
19. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 1)$ ， $B (- 4 ， 5)$ ， $C (- 5 ， 2)$

(1)、画出 $△ A B C$ 关于原点 $O$ 中心对称的 $△ A_{1} B_{1} C_{1}$

(2)、分别写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

查看试题解析
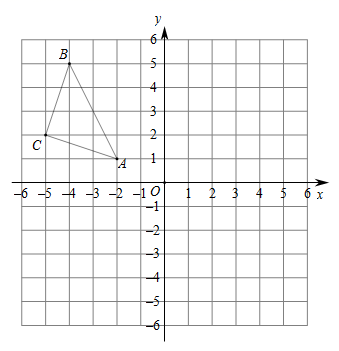20. 如图所示，某幼儿园有一道长为16米的墙，计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD．求该矩形草坪BC边的长．

查看试题解析
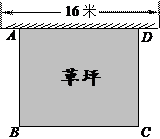21. 如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如果AF=4，AB=7．

(1)、求BE的长；

(2)、在图中作出延长BE与DF的交点G，并说明BG⊥DF．

查看试题解析
22. 某商品现在的售价为每件30元，每星期可卖出160件，市场调查反映，如调整价格，每涨价1元，每星期要少卖出2件.已知商品的进价为每件10元.

(1)、在顾客得到实惠的情况下，如何定价商家才能获得4200元的利润？

(2)、如何定价才能使利润最大？

查看试题解析
23. 如图，直线 $y = - x + 4$ 交 $x$ 轴于点 $A$ ，交 $y$ 轴于点 $C$ ，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点 $A$ ，交 $y$ 轴于点 $B (0, - 2)$ ．点 $D$ 为抛物线上一动点，过点 $D$ 作 $x$ 轴的垂线，交直线 $A C$ 于点 $P$ ，设点 $D$ 的横坐标为 $m$ ．

(1)、求抛物线的解析式；

(2)、当点 $D$ 在直线 $A C$ 下方的抛物线上运动时，求线段 $P D$ 长度的最大值；

(3)、若点 $E$ 是平面内任意一点，是否存在点 $D$ ，使以 $B$ ， $C$ ， $P$ ， $E$ 为顶点的四边形为菱形？若存在，请直接出 $m$ 的值；若不存在，请说明理由．

查看试题解析

x	3.23	3.24	3.25	3.26
$a x^{2} + b x + c$	$\begin{array}{l} - 0.06 \end{array}$	$\begin{array}{l} - 0.02 \end{array}$	0.03	0.07