湖北省武汉市江岸区2023-2024学年八年级上学期数学期中试卷
试卷更新日期:2024-08-19 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)下列各题中均有四个备选答案,其中有且只有一个是正确的,请在答题卡上将正确答案的代号涂黑.
-
1. 2023年全国民航工作会议介绍了2023年民航业发展目标:民航业将按照安全第一、市场主导、保障先行的原则,在做好运行保障能力评估的基础上,把握好行业恢复发展的节奏.下列航空图标,其文字左方的图案是轴对称图形的是( )A、
 春秋航空
B、
春秋航空
B、 东方航空
C、
东方航空
C、 厦门航空
D、
厦门航空
D、 海南航空
2. 下列长度的三条线段首尾相连能组成三角形的是( )A、5,6,10 B、5,2,9 C、5,7,12 D、3,4,83. 一个三角形最多有( )钝角A、0个 B、1个 C、2个 D、3个4. 在平面直角坐标系中,点关于x轴的对称点的坐标是( )A、 B、 C、 D、5. 若一个多边形的外角和与它的内角和相等,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 已知,如图所示的两个三角形全等,则( )
海南航空
2. 下列长度的三条线段首尾相连能组成三角形的是( )A、5,6,10 B、5,2,9 C、5,7,12 D、3,4,83. 一个三角形最多有( )钝角A、0个 B、1个 C、2个 D、3个4. 在平面直角坐标系中,点关于x轴的对称点的坐标是( )A、 B、 C、 D、5. 若一个多边形的外角和与它的内角和相等,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 已知,如图所示的两个三角形全等,则( ) A、 B、 C、 D、7. 如图,用三角尺可按如图方法画角平分线:在已知的的两边上,分别取 , 再分别过点M、N作OA、OB的垂线,交点为P , 画射线OP , 则OP平分 . 做法中用到证明与全等的判定方法是( )
A、 B、 C、 D、7. 如图,用三角尺可按如图方法画角平分线:在已知的的两边上,分别取 , 再分别过点M、N作OA、OB的垂线,交点为P , 画射线OP , 则OP平分 . 做法中用到证明与全等的判定方法是( ) A、SAS B、SSS C、ASA D、HL8. 如图,点E、F在BC上, , . 添加一个条件后,不能证明 , 这个条件可能是( )
A、SAS B、SSS C、ASA D、HL8. 如图,点E、F在BC上, , . 添加一个条件后,不能证明 , 这个条件可能是( ) A、 B、 C、 D、9. 中, , 点M在的内部,BM、MC的垂直平分线分别交AB、AC于点P、Q , 若连接PQ恰好经过点M , 则( )(用含的代数式表示).
A、 B、 C、 D、9. 中, , 点M在的内部,BM、MC的垂直平分线分别交AB、AC于点P、Q , 若连接PQ恰好经过点M , 则( )(用含的代数式表示). A、 B、 C、 D、10. A、B、C为三个小区,A、B、C三个小区的学生人数比为3:7:4,现在要在所在的平面上建造一个学校P , 使得所有学生走的路程和最短,则学校P应该选在( )
A、 B、 C、 D、10. A、B、C为三个小区,A、B、C三个小区的学生人数比为3:7:4,现在要在所在的平面上建造一个学校P , 使得所有学生走的路程和最短,则学校P应该选在( ) A、点C处 B、三条中线的交点处 C、点B处 D、和的角平分线的交点处
A、点C处 B、三条中线的交点处 C、点B处 D、和的角平分线的交点处二、选择题(共6小题,每小题3分,共18分)
-
11. 从五边形的一个顶点出发,可以画出条对角线.12. 如图,中 , 点E , D分别在边AC , AB上,若 , 则 .
 13. 等腰三角形的两边长为5和10,则该等腰三角形的周长为 .14. 如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,则△ABC的周长为.
13. 等腰三角形的两边长为5和10,则该等腰三角形的周长为 .14. 如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,则△ABC的周长为. 15. 如图,在中, , , 点D为AB左侧一点, , , , 则的面积为 .
15. 如图,在中, , , 点D为AB左侧一点, , , , 则的面积为 . 16. 中, , 点D , E在边BC上(点D在点E的左侧), , , 点F在边AC上, , 若 , , , 则 . (用含a , b的式子表示)
16. 中, , 点D , E在边BC上(点D在点E的左侧), , , 点F在边AC上, , 若 , , , 则 . (用含a , b的式子表示)
三、解答题(共8小题,共72分)
-
17. 中, , , 求各内角的度数.18. 如图,点B、E、C、F在一条直线上, , , , 求证: .
 19. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠1=∠2.
19. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠1=∠2.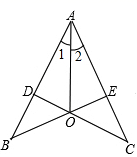 20. 如图,四边形ABCD中, , BE平分 , DF平分 , 设 .
20. 如图,四边形ABCD中, , BE平分 , DF平分 , 设 . (1)、时,求的度数;(2)、证明: .21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.点A、B、C、D都是格点,点P是线段AB上一点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、时,求的度数;(2)、证明: .21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.点A、B、C、D都是格点,点P是线段AB上一点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. (1)、在图1中,画出的中线AM和高线BN;(2)、在图2中,在边AC上取一点E , 使得;(3)、在图3中,在线段AD上取一点Q , 使得 .22. 在中,AO、BO分别平分、 .
(1)、在图1中,画出的中线AM和高线BN;(2)、在图2中,在边AC上取一点E , 使得;(3)、在图3中,在线段AD上取一点Q , 使得 .22. 在中,AO、BO分别平分、 . (1)、如图1,若 , 则;(2)、如图2,连结OC , 求证:OC平分;(3)、如图3,若 , , , 求OB的长.23.
(1)、如图1,若 , 则;(2)、如图2,连结OC , 求证:OC平分;(3)、如图3,若 , , , 求OB的长.23. (1)、问题提出
(1)、问题提出
如图1,已知: , , 探究:BC和DF的数量关系并加以证明;(2)、问题探究
如图2,在中, , 过点C作射线 , 连结BF交边AC于点E , 点D在边AB上,连结DF , 若 , 探究BE和FD的数量关系并加以证明;(3)、问题拓展
如图3,锐角中, , 过点C作直线 , 点E为边AC上一点,连BE并延长交直线l于点F , 点D在边AB上,若 , 直接写出和的数量关系. .24. 在平面直角坐标系中, , (a , b均为正数). (1)、若 , 直接写出A、B两点的坐标;(2)、如图1,在(1)的条件下,点C在x轴的负半轴上, , 点D在BC的延长线上, , 求的值;(3)、如图2,在和中, , , , 射线MO交线段AN于点P . 求证:点P为线段AN的中点.
(1)、若 , 直接写出A、B两点的坐标;(2)、如图1,在(1)的条件下,点C在x轴的负半轴上, , 点D在BC的延长线上, , 求的值;(3)、如图2,在和中, , , , 射线MO交线段AN于点P . 求证:点P为线段AN的中点.