【提高版】浙教版（2024）七上第三章实数单元测试

试卷更新日期：2024-08-15 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知：n $= \sqrt{15}$ ，则估算n的取值范围是（　　）

A、3＜n＜4 B、4＜n＜5 C、5＜n＜6 D、6＜n＜7

查看试题解析
2. 下列说法中正确的是（　　　）

A、 $81$ 的平方根是 $9$ B、 $\sqrt{16}$ 的算术平方根是 $4$ C、 $\sqrt[3]{- a}$ 与 $- \sqrt[3]{a}$ 相等 D、 $64$ 的立方根是 $\pm 4$

查看试题解析
3. 在数轴上， $a$ 所表示的点在 $b$ 所表示的点的左边，且 $| a | = 3$ ， b²=1，则 $a - b$ 的值为（）

A、-2 B、-3 C、－4或-2 D、-2或4

查看试题解析
4. 下列说法中，正确的是（）

A、正整数和负整数统称为整数 B、整数和分数统称为有理数 C、有理数包括正有理数和负有理数 D、有理数包括整数、分数和零

查看试题解析
5. 如图，直径为1个单位长度的圆从A点（A点在数轴上表示的数是1）沿数轴向右滚动一周后到达点B，则点B表示的数是（　　）

A、π B、π+1 C、π﹣1 D、2π

查看试题解析
6. 有一个数值转换器，流程如下：
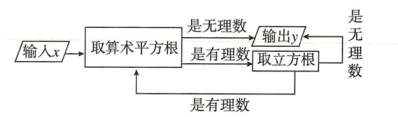
当输人的x值为64时，输出的y值是（）

A、4 B、 $\sqrt{2}$ C、2 D、 $^{3} \sqrt{2}$

查看试题解析
7. 如图，A，B，C三点在数轴上所表示的数分别为a、b、c，根据图中各点位置，下列各式正确的是 $($ $)$

A、 $(a - 1) (b - 1) > 0$ B、 $(c - 1) (b - 1) > 0$ C、 $(a + 1) (b + 1) < 0$ D、 $(c + 1) (b + 1) < 0$

查看试题解析
8. 已知 $a^{2} = 16 ， b^{3} = - 27$ ，且 $| a - b | = a - b$ ，则 $a + b$ 的值为（）

A、1 B、－7 C、－1 D、1或－7

查看试题解析
9. 今年“十一”期间，广州部分公园举行游园活动，据统计，天河公园早晨 $6$ 时 $30$ 分有 $2$ 人进入公园，接下来的第一个 $30$ 分钟内有 $4$ 人进去 $1$ 人出来，第二个 $30$ 分钟内有 $8$ 人进去 $2$ 人出来，第三个 $30$ 分钟内有 $16$ 人进去 $3$ 人出来，第四个 $30$ 分钟内有 $32$ 人进去 $4$ 人出来．按照这种规律进行下去，到上午 $11$ 时 $30$ 分公园内的人数是（）

A、 $2^{11} - 47$ B、 $2^{12} - 57$ C、 $2^{13} - 68$ D、 $2^{14} - 80$

查看试题解析

二、填空题（每题4分，共24分）

10. 计算： $\sqrt{16}$ = ．

查看试题解析
11. $\sqrt{4} + \sqrt[3]{- 8} =$

查看试题解析
12. 如图，实数 $1 - \sqrt{2}$ 在数轴上的对应点可能是点．

查看试题解析
13. 大于 $- \sqrt{5}$ 且小于π的整数有个．

查看试题解析
14. 如图，面积为3的正方形 $A B C D$ 的顶点A在数轴上，对应的数为1，以点A为圆心， $A D$ 长为半径画弧交数轴于点E（点E位于点A的左侧），则线段 $E A =$ ，点E对应的数为．

查看试题解析
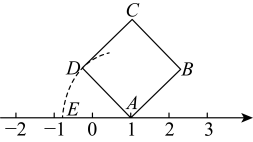15. 根据图中的程序，当输入x为64时，输出的值是．

查看试题解析

三、解答题（共8题，共66分）

16. 把下列各数的序号填在相应的大括号里：
$① - (- 7) ； ② - 2.6 ； ③ - \frac{π}{3} ； ④ | - 2 | ； ⑤ \sqrt{8} ； ⑥ - (\frac{1}{2})_{}^{2} ； ⑦ (- \frac{1}{3})_{}^{3} ；$ $⑧ 0.3030030003 . . .$ （两个“3”之间依次多一个“0”）
非负整数集合：{}；
负分数集合：{}；
无理数集合：{}；

查看试题解析
17. 阅读材料：
题目：请把实数0，-π，-2， $\sqrt{8}$ ，1表示在数轴上，并比较它们的大小（用＜号连接）.

解：

上题是小马同学的作业，老师看了后，找来小马问道：“小马同学，你标在数轴上的两个点对应题中的两个无理数，是吗？”小马点点头.

老师又说：“你这两个无理数对应的点找的非常准确，遗憾的是没有完成全部解答.”

请你帮小马同学完成以下作业：

(1)、补全数轴；

(2)、在数轴上把实数0，-π，-2， $\sqrt{8}$ ，1表示出来，并比较它们的大小（用＜号连接）.

查看试题解析
18. 已知 $5 m - 2$ 的立方根是 $- 3$ ， $3 m + 2 n - 1$ 的算术平方根是4，求 $2 m + n + 10$ 的平方根．

查看试题解析
19. 阅读理解.
$∵ \sqrt{4} < \sqrt{5} < \sqrt{9}$ 即 $2 < \sqrt{5} < 3$

$∴ 1 < \sqrt{5} - 1 < 2$

$∴ \sqrt{5} - 1$ 的整数部分为1，

$∴ \sqrt{5} - 1$ 的小数部分为 $\sqrt{5} - 2$

解决问题：已知a是 $\sqrt{17}$ ﹣3的整数部分，b是 $\sqrt{17}$ ﹣3的小数部分.

(1)、求a，b的值；

(2)、求（﹣a）³+（b+4）²的平方根，提示：（ $\sqrt{17}$ ）²＝17.

查看试题解析
20. 如图1，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形．

(1)、拼成的正方形的面积为，边长为．

(2)、如图2，以数轴的单位长度的线段为边作一个直角三角形，以数轴上表示﹣1的点为圆心，直角三角形的最大边为半径画弧，交数轴正半轴于点A ，那么点A表示的数是．

(3)、如图3，网格中每个小正方形的边长为1，若把阴影部分剪拼成一个正方形，那么新正方形的边长是．

查看试题解析
21. 观察下面图形，每个小正方形的边长为1.

(1)、则图中阴影部分的面积S是，边长a是.

(2)、若a的整数部分为x ，小数部分为y ，求y – x的值.（结果保留根号）

(3)、若数轴上有一点P ，点P所表示的数是 $- 2$ ，请在给出的数轴上画出点P向右移动a个单位长度所到的点Q ，并写出点Q所表示的数为 .

查看试题解析
22. 请回答下列问题：

(1)、 $\sqrt{17}$ 介于连续的两个整数 $a$ 和 $b$ 之间，且 $a < b$ ，那么 $a =$ ， $b =$ ；

(2)、 $x$ 是 $\sqrt{17} + 2$ 的小数部分， $y$ 是 $\sqrt{17} - 1$ 的整数部分，求 $x =$ ， $y =$ ；

(3)、求 ${(\sqrt{17} - x)}^{y}$ 的平方根.

查看试题解析
23. 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、 $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确；
信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5﹣2得来的；
信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如2＜ $\sqrt{5}$ ＜3，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ；
根据上述信息，回答下列问题：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是；

(2)、8+ $\sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为a＜8+ $\sqrt{3}$ ＜b则a+b＝；

(3)、若 $\sqrt{39}$ －2＝a+b，其中a是整数，且0＜b＜1，请求2a-b的相反数．

查看试题解析

【提高版】浙教版（2024）七上第三章 实数 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

【提高版】浙教版（2024）七上第三章实数单元测试