北师大版数学七年级上册《 第四章 基本平面图形》单元提升测试卷
试卷更新日期:2024-08-15 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列生活、生产现象中,可以用基本事实“两点之间,线段最短”来解释的是( )A、利用圆规可以比较两条线段的大小关系 B、用两个钉子就可以把木条固定在墙上 C、把弯曲的河道改直,可以缩短航程 D、连接两点间的线段的长度,叫做这两点之间的距离2. 将一副三角板按下列图示位摆放,其中的是( )A、
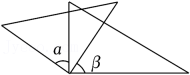 B、
B、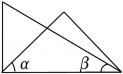 C、
C、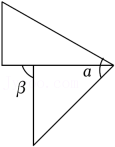 D、
D、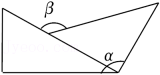 3. 在一条马路边上有间距为10米的甲、乙两棵树,现要在距离甲树4米的地方立一根电线杆,且电线杆与甲、乙两树在同一条直线上,那么电线杆与乙树的距离为( )A、6米 B、14米 C、6米或14米 D、4米或6米4. 如图,点为直线上一点,平分 , , 若 , 则的度数为( )
3. 在一条马路边上有间距为10米的甲、乙两棵树,现要在距离甲树4米的地方立一根电线杆,且电线杆与甲、乙两树在同一条直线上,那么电线杆与乙树的距离为( )A、6米 B、14米 C、6米或14米 D、4米或6米4. 如图,点为直线上一点,平分 , , 若 , 则的度数为( )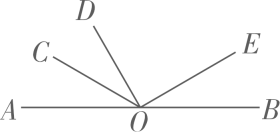 A、 B、 C、 D、5. 如图, 2 时整, 钟表的时针和分针所成的锐角为( )
A、 B、 C、 D、5. 如图, 2 时整, 钟表的时针和分针所成的锐角为( ) A、 B、 C、 D、6. n边形所有对角线的条数有( )A、 条 B、 条 C、 条 D、 条7. 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=( )
A、 B、 C、 D、6. n边形所有对角线的条数有( )A、 条 B、 条 C、 条 D、 条7. 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=( ) A、40° B、60° C、120° D、135°8. 如图,将一根木棒的一端固定在点,另一端绑一重物.将此重物拉到点后放开,让此重物由点摆动到点.则此重物移动路径的形状为( )
A、40° B、60° C、120° D、135°8. 如图,将一根木棒的一端固定在点,另一端绑一重物.将此重物拉到点后放开,让此重物由点摆动到点.则此重物移动路径的形状为( ) A、倾斜直线 B、抛物线 C、圆弧 D、水平直线9. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm10. 如图,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是( )
A、倾斜直线 B、抛物线 C、圆弧 D、水平直线9. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm10. 如图,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是( ) A、2πcm B、4πcm C、8πcm D、16πcm
A、2πcm B、4πcm C、8πcm D、16πcm二、填空题(每题3分,共18分)
-
11. 如图,点C,D在线段AB上,AC=BD,若AD=8cm,则BC=cm.
 12. 把一副三角尺按如图所示拼在一起,其中 , , 三点在同一直线上, 平分 , 平分 ,则 .
12. 把一副三角尺按如图所示拼在一起,其中 , , 三点在同一直线上, 平分 , 平分 ,则 .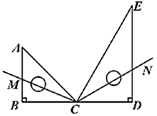 13. 如图,点 , 是直线 上的两点,点 , 在直线 上且点 在点 的左侧,点 在点 的右侧, , .若 ,则 .
13. 如图,点 , 是直线 上的两点,点 , 在直线 上且点 在点 的左侧,点 在点 的右侧, , .若 ,则 . 14. 如图所示,是直线上一点,是一条射线,平分 , 在内, , , 则的度数是 .
14. 如图所示,是直线上一点,是一条射线,平分 , 在内, , , 则的度数是 .
 15. 如图,点是线段上的三个点,已知 , 则图中所有线段的和为 .
15. 如图,点是线段上的三个点,已知 , 则图中所有线段的和为 . 16. 如图,C为直线上一点,为直角,平分 , 平分 , 平分 , 则.
16. 如图,C为直线上一点,为直角,平分 , 平分 , 平分 , 则.
三、解答题(共8题,共72分)
-
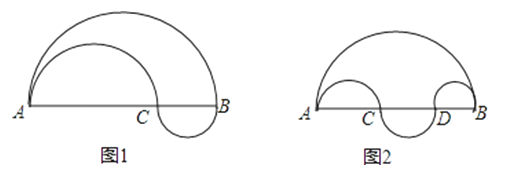
17. (1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲、乙走的路程图改成图2,两人走的路程远近相同吗?
 18. A、B、C、D四个站的位置如图所示.
18. A、B、C、D四个站的位置如图所示. (1)、分别表示出A、D两站之间的距离和A、C两站之间的距离;(2)、若 , C为的中点,求b的值.19. 如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.
(1)、分别表示出A、D两站之间的距离和A、C两站之间的距离;(2)、若 , C为的中点,求b的值.19. 如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.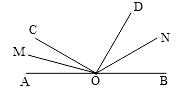 (1)、知∠AOC=40°,∠BOD=60°,求∠MON的度数;(2)、知∠COD=90°,求出∠MON的度数.20. 将线段AB延长至C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8cm.
(1)、知∠AOC=40°,∠BOD=60°,求∠MON的度数;(2)、知∠COD=90°,求出∠MON的度数.20. 将线段AB延长至C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8cm.(1)求AB的长度;
(2)如果点M是线段AB中点,点N是线段AE中点,求MN的长度.
21. 如图,OB为∠AOC的平分线,OD是∠COE的平分线.(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
 22. 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足 , 若P是线段上任意一点,C、D两点分别从点P、B开始出发,同时向点A运动,如果点C的运动速度为2cm/s,点D的运动速度为3cm/s.运动的时间为ts.
22. 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足 , 若P是线段上任意一点,C、D两点分别从点P、B开始出发,同时向点A运动,如果点C的运动速度为2cm/s,点D的运动速度为3cm/s.运动的时间为ts. (1)、求线段的长;(2)、若 ,
(1)、求线段的长;(2)、若 ,①当C、D两点运动1s后,求线段的长;
②当C、D两点运动ts后,且点D在线段上时,用含t的代数式表示线段、的长,并说明与的数量关系.
(3)、如果 , .试探索线段的长.23. 如图,已知同一平面内,∠AOB=90゜,∠AOC=60゜.(1) 求∠COB ;
(2)如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为 ;
(3)试问在(2)的条件下,如果将题目中∠AOC=60゜改成∠AOC=2α(α<45゜),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
 24. 已知:点M,N分别是线段AC,BC的中点.
24. 已知:点M,N分别是线段AC,BC的中点.(1)如图,点C在线段AB上,且AC=9cm,CB=6cm,求线段MN的长;
(2)若点C为线段AB上任一点,且AC=acm,CB=bcm,用含有a,b的代数式表示线段MN的长度.
(3)若点C在线段AB的延长线上,且AC=acm,CB=bcm,请你画出图形,并且用含有a,b的代数式表示线段MN的长度.
