【培优版】浙教版（2024）七上3.2实数同步练习

试卷更新日期：2024-08-15 类型：同步测试

进入出卷网下载

一、选择题

1. 在实数3.14， $\sqrt{0.04}$ ， $\frac{2}{9}$ ， $\frac{π}{2}$ 中，属于无理数的是（）

A、3.14 B、 $\sqrt{0.04}$ C、 $\frac{2}{9}$ D、 $\frac{π}{2}$

查看试题解析
2. 数轴上点A表示的数是1，点B，C分别位于点A的两侧，且到点A的距离相等．若点B表示的数是 $\sqrt{2}$ ，则点C表示的数是（）

A、 $- \sqrt{2}$ B、 $\sqrt{2}$ -1 C、2- $\sqrt{2}$ D、 $\sqrt{2}$ -2

查看试题解析
3. 对于0的表述，不正确的是（）

A、0是自然数 B、相反数是本身的数只有0 C、0的平方根是本身 D、0既不是有理数也不是无理数

查看试题解析
4. 估算 $\sqrt{13}$ +1的范围为（）

A、在1到2之间 B、在2到3之间 C、在3到4之间 D、在4到5之间

查看试题解析
5. 若 $| a | = - a$ ， $a$ 一定是（）

A、正数 B、负数 C、非正数 D、非负数

查看试题解析
6. 如图，圆的直径为2个单位长度，该圆上的点 $A$ 与数轴上表示 $- 1$ 的点重合，将圆沿数轴向左无滑动地滚动一周，点 $A$ 到达点 $A^{'}$ 的位置，则点 $A^{'}$ 表示的数是（）

A、 $2 π - 1$ B、 $- 2 π - 1$ C、 $π - 1$ D、 $- π - 1$

查看试题解析
7. 下列说法中：
$① 0$ 是最小的整数；
$②$ 有理数不是正数就是负数；
$③$ 正整数、负整数、正分数、负分数统称为有理数；
$④$ 非负数就是正数；
$⑤ - \frac{π}{2}$ 不仅是有理数，而且是分数；
$⑥$ 带“ $-$ ”号的数一定是负数；
$⑦$ 无限小数不都是有理数；
$⑧$ 正数中没有最小的数，负数中没有最大的数．
其中错误的说法的个数为（）

A、 $7$ 个 B、 $6$ 个 C、 $5$ 个 D、 $4$ 个

查看试题解析

二、填空题

8. 这三个数 $- \sqrt{3}$ 、 $- \frac{1}{3}$ 、 $- 1$ 中，最小的数是.

查看试题解析
9. 与 $\sqrt{34}$ 最接近的整数是．

查看试题解析
10. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $c$ 是 $\sqrt{17}$ 的整数部分，则 $a + c$ 的值为．

查看试题解析
11. 如图，数轴上点A ， B对应的数分别是1，2，以AB为边在数轴上方作正方形ABCD ，连接AC ，以A为圆心，AC的长为半径画圆弧交数轴于点E（点E在点A的左侧），则点E在数轴上对应的数为．

查看试题解析

三、解答题

12. 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如： $π$ 、 $\sqrt{2}$ 等，而常用的“ $\dots$ ”或者“ $\approx$ ”的表示方法都不够百分百准确；
信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5-2得来的；
信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ；
根据上述信息，回答下列问题：

(1)、 $\sqrt{13}$ 的整数部分是，小数部分是；

(2)、若 $21 < a < 22$ ，则 $a$ 的整数部分是；小数部分可以表示为；

(3)、 $10 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 10 + \sqrt{3} < b$ 则 $a + b =$ ；

(4)、若 $\sqrt{30} - 3 = x + y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，请求 $x - y$ 的相反数.

查看试题解析
13. 如图，有这样一个探究：把两个边长为1的小正方形分别沿对角线剪开，将所得的4个直角三角形拼在一起，可以得到一个面积为2的大正方形，试根据这个研究方法回答下列问题：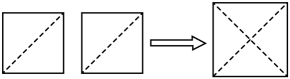

(1)、所得到的面积为2的大正方形的边长就是原边长为1的小正方形的对角线长，因此可得小正方形的对角线长为；

(2)、由此我们得到一种在数轴上找到无理数的方法：如下图，以单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于 $A$ 、 $B$ 两点，那么 $A$ 点表示的数为；

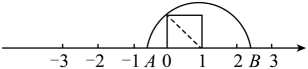(3)、通过动手操作，漠子同学把长为5，宽为1的长方形进行裁剪，拼成如图所示的正方形．请借鉴（2）中的方法在数轴上找到表示 $\sqrt{5} - 1$ 的点 $P$ ．（保留作图痕迹并标出必要线段长）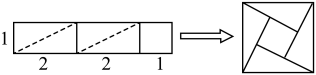

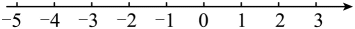查看试题解析
14.

(1)、【基本事实】
我们知道整数和分数统称为有理数，为什么不是整数和小数统称为有理数呢？所有的分数都可以化成小数的形式，是不是所有的小数都可以化成分数形式呢？我们可以举例说明：有限小数0.2化成分数的形式是；无限循环小数又该如何化呢？我们以无限循环小数0.7为例进行说明：设 $0 . \overset{•}{7}$ ＝x，由 $0 . \overset{•}{7}$ ＝0.7777…可知，10x＝7.7777…，所以10x＝7+x，解方程，得x＝ $\frac{7}{9}$ ，于是得 $0 . \overset{•}{7} = \frac{7}{9}$ ，故 $0 . \overset{•}{3} \overset{•}{7}$ 化成分数的形式是，所有有限小数和无限循环小数（填“是”或“不是”）有理数；而无限不循环小数是不可以化成分数的，所以π （填“是”或“不是”）有理数，那么无限不循环小数能通过数轴上的一个点来表示吗？我们将以π为例通过下列活动来探索：

(2)、【数学活动】
如图，直径为1的圆从原点出发沿数轴正方向滚动一周，圆上一点由原点O到达点O'，则OO′＝．

(3)、【知识推理】
判断：（填“正确”或“错误”）
①任何一个有理数都可以用数轴上唯一的一个点来表示．
②数轴上的点都表示有理数．
③整数和小数统称为有理数．

查看试题解析

【培优版】浙教版（2024）七上3.2实数 同步练习

一、选择题

二、填空题

三、解答题

【培优版】浙教版（2024）七上3.2实数同步练习