广西崇左市宁明县2023-2024学年八年级下学期数学期末试卷
试卷更新日期:2024-08-14 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 要使有意义,则的值可以是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 若关于x的方程(m+2)x2-3x+1=0是一元二次方程,则m的取值范围是( )A、m≠0 B、m>-2 C、m≠-2 D、m>04. 矩形、菱形、正方形共有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相垂直平分 D、对角线互相平分5. 若3、4、a为勾股数,则a的值为( )A、 B、5 C、5或7 D、5或6. 正十二边形的外角和为( )A、30° B、150° C、360° D、1800°7. “冬季奥林匹克运动会”的英语是“”,其中字母“”出现的频率是( )A、 B、 C、 D、8. 某中学开展“读书节活动”,该中学某语文老师随机抽样调查了本班10名学生平均每周的课外阅读时间,统计如表:
每周课外阅读时间(小时)
学生数(人)
下列说法错误的是( )
A、众数是 B、平均数是 C、样本容量是 D、中位数是9. 在▱中,对角线 , 相交于点 , 下列判断中错误的是( )A、若 , 则▱为矩形 B、若平分 , 则▱为菱形 C、若 , 则▱为菱形 D、若 , 则▱为正方形10. 若一元二次方程mx2+2x+1=0有实数解,则m的取值范围是( )A、m≥-1 B、m≤1 C、m≥-1且m≠0 D、m≤1且m≠011. 已知 , 则化简的结果是( )A、 B、 C、 D、12. 如图,在矩形ABCD中对角线AC与BD相交于点O, ,垂足为点E, ,且 ,则AD的长为( )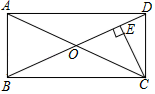 A、 B、 C、10 D、
A、 B、 C、10 D、二、填空题:本题共6小题,每小题2分,共12分。
-
13. 在实数范围内分解因式: .14. 已知一个多边形的内角和为540°,则这个多边形是边形.15. 若 , 是一元二次方程的两个实数根,则 .16. 如图所示,在平行四边形中, , , 的平分线交线段于点E,则 .
 17. 有两个合唱队,各有名队员组成,甲队与乙队的平均身高均为 , 甲队身高的方差 , 乙队身高的方差 , 则两队身高比较整齐的是队18. 观察下列等式:
17. 有两个合唱队,各有名队员组成,甲队与乙队的平均身高均为 , 甲队身高的方差 , 乙队身高的方差 , 则两队身高比较整齐的是队18. 观察下列等式:第个等式:;第个等式:;第个等式:; , 按照以上规律,写出第个等式 .
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
19. 计算及解方程.(1)、计算:;(2)、解方程 .20. 如图所示为一块铁皮,测得 , , , , , 求这块铁皮的面积.
 21. 已知关于的一元二次方程 , 其中、、分别为三边的长.(1)、如果是方程的根,试判断的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断的形状,并说明理由.22. 学校组织七、八年级学生参加了“国家安全知识”测试已知七、八年级各有人,现从两个年级分别随机抽取名学生的测试成绩单位:分进行统计:
21. 已知关于的一元二次方程 , 其中、、分别为三边的长.(1)、如果是方程的根,试判断的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断的形状,并说明理由.22. 学校组织七、八年级学生参加了“国家安全知识”测试已知七、八年级各有人,现从两个年级分别随机抽取名学生的测试成绩单位:分进行统计:
七年级
八年级
整理如下:年级
平均数
中位数
众数
方差
七年级
八年级
根据以上信息,回答下列问题:
(1)、填空: , ;同学说:“这次测试我得了分,位于年级中等偏上水平”,由此可判断他是年级的学生;
(2)、学校规定测试成绩不低于分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数;(3)、你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.23. 点为平行四边形中边的延长线上的一点,且 , 连接分别交、于点、 , 连接交于点 , 连接 .
求证: .
24. 阅读下面的材料,然后解答问题:, ,
以上这种化简的步骤叫作分母有理化.
还可以用以下方法化简:
(1)、化简: , ;(2)、参照式化简:;(3)、参照式化简: .25. 某童装专卖店在销售中发现,一款童装每件的进价为元,当销售单价为元时,每天可售出件为了迎接六一儿童节,该专卖店决定采取适当的降价措施,以最大限度地扩大销售量,减少库存,增加利润据测算,每件童装每降价元,平均每天可多售出件,设每件童装降价元.(1)、每天可售出件,每件盈利元用含的代数式表示(2)、当每件童装降价多少元时,平均每天盈利元?(3)、平均每天的盈利能否达到元?请说明理由.26. 如图,在中, , 过点的直线 , 为边上一点,过点作 , 垂足为 , 交直线于点 , 连接 , . (1)、求证: .(2)、当为的中点,四边形是什么特殊四边形?请说明理由.(3)、若为的中点,则当的度数是多少时,四边形是正方形?请说明理由.
(1)、求证: .(2)、当为的中点,四边形是什么特殊四边形?请说明理由.(3)、若为的中点,则当的度数是多少时,四边形是正方形?请说明理由.