北师大版（2024）数学七年级上册《第五章一元一次方程》单元同步测试卷

试卷更新日期：2024-08-13 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列方程中，是一元一次方程的是（）

A、 $x^{2} - 4 x = 3$ B、 $3 x - 1 = \frac{x}{2}$ C、 $x + 2 y = 1$ D、 $x y - 3 = 5$

查看试题解析
2. 如果方程 $(m - 1) x^{| m |} + 2 = 0$ 是关于 $x$ 的一元一次方程，那么 $m$ 的值是（）

A、 $\pm 1$ B、0 C、 $- 1$ D、1

查看试题解析
3. 把方程 $3 x + \frac{2 x - 1}{3} = 3 - \frac{x + 1}{2}$ 去分母正确的是（）

A、 $18 x + 2 (2 x - 1) = 18 - 3 (x + 1)$ B、 $3 x + (2 x - 1) = 3 - (x + 1)$ C、 $18 x + (2 x - 1) = 18 - (x + 1)$ D、 $3 x + 2 (2 x - 1) = 3 - 3 (x + 1)$

查看试题解析
4. 运用等式性质进行的变形，不正确的是（）

A、如果a=b，那么a-c=b-c B、如果a=b，那么a+c=b+c C、如果a=b，那么 $\frac{a}{c} = \frac{b}{c}$ D、如果a=b，那么ac=bc

查看试题解析
5. 等式就像平衡的天平，能与如图的事实具有相同性质的是（）

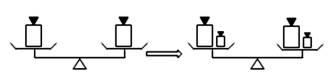A、如果 $a = b$ ，那么 $a c = b c$ B、如果 $a = b$ ，那么 $\frac{a}{c} = \frac{b}{c} (c \neq 0)$ C、如果 $a = b$ ，那么 $a + c = b + c$ D、如果 $a = b$ ，那么 $a^{2} = b^{2}$

查看试题解析
6. 下列解一元一次方程的过程正确的是（）

A、若 $4 x - 3 = 5$ ，则 $4 x = 5 - 3$ B、若 $4 x + 1 = 3 x + 2$ ，则 $4 x - 3 x = 2 + 1$ C、若 $- 5 x = 3$ ，则 $x = - \frac{3}{5}$ D、若 $\frac{x - 1}{2} - 1 = \frac{x}{3}$ ，则 $3 (x - 1) - 1 = 2 x$

查看试题解析
7. 某同学解方程 $4 x - 3 = □ x + 1$ 时，把“ $□$ ”处的系数看错了，解得 $x = 4$ ，他把“ $□$ ”处的系数看成了（）

A、-3 B、3 C、-4 D、4

查看试题解析
8. 《孙子算经》是中国古代重要的数学著作，是《算经十书》之一.书中记载了这样一个题目：今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺.问木长多少尺？设木长x尺，则可列方程为（）

A、 $\frac{1}{2} (x + 4.5) = x - 1$ B、 $\frac{1}{2} (x + 4.5) = x + 1$ C、 $\frac{1}{2} (x + 1) = x - 4.5$ D、 $\frac{1}{2} (x - 1) = x + 4.5$

查看试题解析
9. 某新能源车企今年5月交付新车35060辆，且今年5月交付新车的数量比去年5月交付的新车数量的1.2倍还多1100辆．设该车企去年5月交付新车 $x$ 辆，根据题意，可列方程为（）

A、 $1.2 x + 1100 = 35060$ B、 $1.2 x - 1100 = 35060$ C、 $1.2 (x + 1100) = 35060$ D、 $x - 1100 = 35060 \times 1.2$

查看试题解析
10. 某工程甲单独完成要45天，乙单独完成要30天，若乙先单独干22天，剩下的由甲单独完成．问甲、乙一共用几天可以完成全部工作，若设甲、乙共用x天完成，则符合题意的方程是（）

A、 $\frac{x - 22}{45} + \frac{22}{30}$ =1 B、 $\frac{x + 22}{30} + \frac{22}{45}$ =1 C、 $\frac{x + 22}{45} + \frac{22}{30}$ =1 D、 $\frac{x}{30} + \frac{x - 22}{45}$ =1

查看试题解析

二、填空题（每题3分，共18分）

11. 请列举一个方程，使它满足未知数系数为 $- 2$ ，未知数的解为3，这个方程可以为．

查看试题解析
12. 当x=时，代数式4x-5与3x-6的值互为相反．

查看试题解析
13. 我国的《洛书》中记载着世界最古老的一个幻方：将九个数字填入 $3 \times 3$ 的方格中，使三行、三列、两对角线上的三个数之和都相等，根据如图的幻方，则代数式 $x - 3 y =$ ．

x

$2 y$

-2

y

0

查看试题解析
14. $x$ 等于数时，代数式 $\frac{3 x - 2}{3}$ 的值比 $\frac{4 x - 1}{4}$ 的值的 $2$ 倍小 $1$ .

查看试题解析
15. 在元朝朱世杰所著的《算术启蒙》中，记载了一道题，大意是：快马每天行240里，慢马每天行150里，慢马先行12天，则快马追上慢马需要的天数是．

查看试题解析
16. 中国古代以算筹为工具来记数、列式和进行各种数与式的演算．《九章算术》第八章名为“方程”，其中有一例为：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，即可表示方程 $x + 4 y = 23$ ，则表示的方程是.

查看试题解析

三、解答题（共8题，共72分）

17. 解下列方程：

(1)、 $2 (1 - 2 x) = 5 x + 8$

(2)、 $\frac{2 x + 1}{3} = 1 - \frac{x - 1}{4}$ ．

查看试题解析
18. 解方程

(1)、 $3 x - 4 = 2 x + 5$

(2)、 $\frac{2 x - 5}{6} - \frac{3 - x}{4} = 1$

查看试题解析
19. 解方程：

(1)、 $2 (x - 3) = 3 x - 1$ ；

(2)、 $\frac{2 x - 1}{3} - 3 = \frac{x + 1}{2} - x$

查看试题解析
20. 解方程：

(1)、2x+1＝﹣x+3；

(2)、 $\frac{2 - x}{2} - 3 = \frac{x}{3} - \frac{2 x + 3}{6}$ ．

查看试题解析
21. 已知a－2(4－x)＝5a是关于x的方程，且与方程6－x＝ $\frac{x + 3}{2}$ 有相同的解．

(1)、求a的值．

(2)、求多项式 $\frac{8 a_{}^{2} - 2 a + 7}{- 5}$ 的值．

查看试题解析
22. 将飞镖投向如图所示的靶盘．计分规则如下：每次投中A区得5分，投中B区得3分，脱靶扣2分．小曹玩了两局，每局投10次飞镖，在第一局中，小曹投中A区2次，B区4次，脱靶4次．

(1)、求小曹第一局的得分，

(2)、第二局，小曹投中A区k次，B区5次，其余全部脱靶．若小曹第二局得分比第一局得分提高了12分，求k的值．

查看试题解析
23. 小明用长方形硬纸板做底面为正方形的长方体盒子，他用如图两种方法进行裁剪．
A方法：剪3个侧面；B方法：剪2个侧面和2个底面，
现有35张硬纸板，其中x张用A方法裁剪，其余用B方法裁剪．

(1)、A方法裁剪出侧面的个数为个；
B方法裁剪出侧面的个数为个，底面共有个；
（用含x的代数式表示，结果要求化简）

(2)、若用（1）中裁剪出的侧面和底面做长方体盒子，恰好全部用完，求共做了多少个盒子？

查看试题解析
24. 某市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：
用水量/月
单价（元/m³）
不超过20 m³
2.05
超过20 m³的部分
3.05
另：每立方米用水加收0.8元的城市污水处理费和0.15元的城市附加费

(1)、根据上表，用水量每月不超过20 m³ ，实际每立方米收水费多少元？如果10月份某用户用水量为18 m³ ，那么该用户10月份应该缴纳水费多少元？

(2)、某用户11月份共缴纳水费80元，那么该用户11月份用水多少立方米？

(3)、若该用户水表12月份出了故障，有25%的水量没有计入水表中，这样该用户在12月份只缴纳了54元水费，问该用户12月份实际应该缴纳水费多少元？

查看试题解析

用水量/月	单价（元/m³）
不超过20 m³	2.05
超过20 m³的部分	3.05
另：每立方米用水加收0.8元的城市污水处理费和0.15元的城市附加费

北师大版（2024）数学七年级上册《 第五章 一元一次方程》单元同步测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版（2024）数学七年级上册《第五章一元一次方程》单元同步测试卷