湘教版数学八年级上册《第5章二次根式》单元提升测试卷

试卷更新日期：2024-08-13 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 若式子 $\sqrt{2 m - 3}$ 有意义，则 $m$ 的取值范围是（）

A、 $m ⩽ \frac{2}{3}$ B、 $m ⩾ - \frac{3}{2}$ C、 $m ⩾ \frac{3}{2}$ D、 $m ⩽ - \frac{2}{3}$

查看试题解析
2. 已知实数 $a$ 在数轴上的对应点位置如图所示，则化简 $| a - 1 | - \sqrt{{(a - 2)}^{2}}$ 的结果是（）

A、 $3 - 2 a$ B、 $- 1$ C、1 D、 $2 a - 3$

查看试题解析
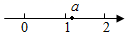3. 下列各组数中，互为相反数的是（　　）

A、 $- 2$ 与 $\sqrt{{(- 2)}^{2}}$ B、 $- 2$ 与 $\sqrt[3]{- 8}$ C、 $2$ 与 ${(\sqrt{- 2})}^{2}$ D、 $| - \sqrt{2} |$ 与 $\sqrt{2}$

查看试题解析
4. 已知a= $\sqrt{2}$ -1，b= $\frac{1}{\sqrt{2} + 1}$ ，则a与b的关系（　　）

A、a=b B、ab=1 C、a=-b D、ab=-1

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ C、 $2 \div \sqrt{2} = 1$ D、 $\sqrt{(- 5)^{2}} = - 5$

查看试题解析
6. 已知 $1 < x < 2$ ，化简 $\sqrt{{(x - 1)}^{2}} + | x - 2 |$ 的结果为（）

A、 $- 1$ B、1 C、 $2 x - 3$ D、 $3 - 2 x$

查看试题解析
7. 已知 $a 、 b$ 是实数，且 $b = 3 + \sqrt{1 - 4 a} - \sqrt{4 a - 1}$ ，则 $\sqrt{a b}$ 的值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{1}{2}$

查看试题解析
8. 若 $a_{n} = 1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}$ （n为正整数），则下列说法正确的个数是（　　）
① ${\sqrt{a}}_{1} = 1 \frac{1}{2} ， \sqrt{a_{2}} = 1 \frac{1}{6} ， \sqrt{a_{3}} = 1 \frac{1}{12}$ ；
② $\sqrt{a_{4}} = 1 + \frac{1}{4} - \frac{1}{5}$ ；
③ $\sqrt{a_{1}} + \sqrt{a_{2}} + \sqrt{a_{3}} + ⋯ + \sqrt{a_{8}} = 8 \frac{8}{9}$ ．

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 观察下列二次根式的化简
S₁= $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2}$
S₂= $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = (1 + \frac{1}{1} - \frac{1}{2}) + (1 + \frac{1}{2} - \frac{1}{3})$
S₃= $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = (1 + \frac{1}{1} - \frac{1}{2}) + (1 + \frac{1}{2} - \frac{1}{3}) + (1 + \frac{1}{3} - \frac{1}{4})$ ，则 $\frac{S_{2023}}{2023}$ =（）

A、 $\frac{1}{2022}$ B、 $\frac{2022}{2021}$ C、 $\frac{2024}{2023}$ D、 $\frac{2025}{2024}$

查看试题解析
10. “分母有理化”是我们常用的一种化简的方法，如： $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 7 + 4 \sqrt{3}$ ，除此之外，我们也可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，设x= $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，易知 $\sqrt{3 + \sqrt{5}}$ > $\sqrt{3 - \sqrt{5}}$ ，故x>0，由x²= ${(\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}})}^{2}$ = $3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})}$ =2，解得x= $\sqrt{2}$ ，即 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}} = \sqrt{2}$ 。根据以上方法，化简 $\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}} + \sqrt{6 - 3 \sqrt{3}} - \sqrt{6 + 3 \sqrt{3}}$ 后的结果为（）

A、5+3 $\sqrt{6}$ B、5+ $\sqrt{6}$ C、5- $\sqrt{6}$ D、5-3 $\sqrt{6}$

查看试题解析

二、填空题（每题3分，共18分）

11. 若 $m$ ， $n$ 为实数，且 ${(m + 4)}^{2} + \sqrt{n - 5} = 0$ ，则 ${(m + n)}^{2}$ 的值为.

查看试题解析
12. 已知 $a ， b$ 为实数，且满足 $\sqrt{a - 8} + \sqrt{8 - a} = b -$ 2，则 $\sqrt{a b}$ 的值是.

查看试题解析
13. 观察： $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{2 + \sqrt{3}} = 2 - \sqrt{3}$ ， $\frac{1}{\sqrt{5} + 2} = \sqrt{5} - 2$ ， $⋯ ⋯$
计算： $1 + \frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{2 + \sqrt{3}} + \frac{1}{\sqrt{5} + 2} + \cdot \cdot \cdot + \frac{1}{\sqrt{2024} + \sqrt{2023}}$ = ．

查看试题解析
14. 已知xy=3，那么 $x \sqrt{\frac{y}{x}} + y \sqrt{\frac{x}{y}}$ 的值为 .

查看试题解析
15. 已知x＝ $\frac{1}{3 - 2 \sqrt{2}}$ ， y＝ $\frac{1}{3 + 2 \sqrt{2}}$ ， $\frac{x}{y} + \frac{y}{x} - 4$ = ．

查看试题解析
16. 观察下列等式：
① $\frac{1}{\sqrt{3} + 1} = \frac{\sqrt{3} - 1}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{\sqrt{3} - 1}{2}$ ；

② $\frac{1}{\sqrt{5} + \sqrt{3}} = \frac{\sqrt{5} - \sqrt{3}}{(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})} = \frac{\sqrt{5} - \sqrt{3}}{2}$

③ $\frac{1}{\sqrt{7} + \sqrt{5}} = \frac{\sqrt{7} - \sqrt{5}}{(\sqrt{7} + \sqrt{5}) (\sqrt{7} - \sqrt{5})} = \frac{\sqrt{7} - \sqrt{5}}{2}$

…

参照上面等式计算方法计算：

$\frac{1}{1 + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{5}} + \frac{1}{\sqrt{5} + \sqrt{7}} + \dots + \frac{1}{3 \sqrt{11} + \sqrt{101}} =$ .

查看试题解析

三、解答题（共10题，共72分）

17. 计算： $\sqrt{27} \div \frac{\sqrt{3}}{2} \times 2 \sqrt{2} - 6 \sqrt{2}$ ．

查看试题解析
18. 计算： $\sqrt[3]{8} + \frac{1}{2 + \sqrt{5}} - {(\frac{1}{3})}^{- 2} + | \sqrt{5} - 3 |$

查看试题解析
19. 计算： $2 \sqrt{a b^{3}} \times \frac{3}{4} \sqrt{a^{3} b} \div 3 \sqrt{\frac{1}{a}}$

查看试题解析
20. 计算： $\frac{2}{m} \sqrt{m^{2} n} \times (\frac{3}{2} \sqrt{m n^{2}}) \div (\frac{1}{3} \sqrt{\frac{m}{n}}) \begin{matrix} (m > 0) \end{matrix}$ ．

查看试题解析
21. 已知 $a = \frac{1}{\sqrt{3} - 1}$ ， $b = \frac{1}{\sqrt{3} + 1}$ ，求 $\sqrt{a b} (\sqrt{\frac{a}{b}} + \sqrt{\frac{b}{a}})$ 的值．

查看试题解析
22. 实数a，b，c在数轴上如图所示，化简：（ $\sqrt{c}$ ）²﹣ $\sqrt{(a + b)^{2}}$ +|b﹣c|+ $\sqrt{(c - a)^{2}}$ ．

查看试题解析
23. 实数a、b、c在数轴上的对应点位置如图所示，化简： $\sqrt{{(- c)}^{2}} + | a - b | + \sqrt[3]{{(a + b)}^{3}} - | b - c |$

查看试题解析
24. 阅读下列解题过程∶
$\frac{1}{\sqrt{7} + \sqrt{6}} = \frac{1 \times (\sqrt{7} - \sqrt{6})}{(\sqrt{7} + \sqrt{6}) (\sqrt{7} - \sqrt{6})} = \frac{\sqrt{7} - \sqrt{6}}{{(\sqrt{7})}^{2} - {(\sqrt{6})}^{2}} = \sqrt{7} - \sqrt{6}$
请回答下列问题∶

(1)、仿照上面的解题过程化简∶ $\frac{1}{\sqrt{6} + \sqrt{5}} =$ $=$ $=$ ．

(2)、请直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ 的化简结果∶ ．

(3)、利用上面所提供的想法，求 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + . . . . . . . + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ 的值．

(4)、利用上面的结论，不计算近似值，试比较 $(\sqrt{12} - \sqrt{11})$ 与 $(\sqrt{13} - \sqrt{12})$ 的大小，并说明理由．

查看试题解析
25. 我们以前学过完全平方公式 $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ ，现在，又学习了二次根式，那么所有的非负数都可以看作是一个数的平方，如 $3 = (\sqrt{3})^{2}$ ， $5 = (\sqrt{5})^{2}$ ，下面我们观察： $(\sqrt{2} - 1)^{2} = (\sqrt{2})^{2} - 2 \times 1 \times \sqrt{2} + 1^{2} = 2 - 2 \sqrt{2} + 1 = 3 - 2 \sqrt{2}$ ．
反之， $3 - 2 \sqrt{2} = 2 - 2 \sqrt{2} + 1 = (\sqrt{2} - 1)^{2}$
$∵ 3 - 2 \sqrt{2} = (\sqrt{2} - 1)^{2}$ $∴ \sqrt{3 - 2 \sqrt{2}} = \sqrt{2} - 1$ ．
仿上例，求：

(1)、 $\sqrt{4 - 2 \sqrt{3}}$ ；

(2)、计算： $\sqrt{3 - 2 \sqrt{2}} + \sqrt{5 - 2 \sqrt{6}} + \sqrt{7 - 2 \sqrt{12}} + \dots \dots + \sqrt{19 - 2 \sqrt{90}}$ ；

(3)、若 $a = \frac{1}{\sqrt{2} - 1}$ ，则求 $4 a^{3} - 9 a^{2} - 2 a + 1$ 的值．

查看试题解析
26. 【阅读材料】阅读下列材料，然后回答问题：
$①$ 在进行二次根式的化简与运算时，我们有时会碰上如 $\frac{2}{\sqrt{3} + 1}$ 一样的式子，其实我们还可以将其进一步化简： $\frac{2}{\sqrt{3} + 1} = \frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{(\sqrt{3})^{2} - 1} = \frac{2 (\sqrt{3} - 1)}{2} = \sqrt{3} - 1$ ，以上这种化简的步骤叫做分母有理化．
$②$ 学习数学，最重要的是学习数学思想，其中一种数学思想叫做换元的思想，它可以简化我们的计算，比如我们熟悉的下面这个题：已知 $a + b = 2$ ， $a b = - 3$ ，求 $a^{2} + b^{2} .$ 我们可以把 $a + b$ 和 $a b$ 看成是一个整体，令 $x = a + b$ ， $y = a b$ ，则 $a^{2} + b^{2} = (a + b)^{2} - 2 a b = x^{2} - 2 y = 4 + 6 = 10 .$ 这样，我们不用求出 $a$ ， $b$ ，就可以得到最后的结果．

(1)、计算： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots + \frac{1}{\sqrt{2023} + \sqrt{2021}}$ ；

(2)、 $m$ 是正整数， $a = \frac{\sqrt{m + 1} - \sqrt{m}}{\sqrt{m + 1} + \sqrt{m}}$ ， $b = \frac{\sqrt{m + 1} + \sqrt{m}}{\sqrt{m + 1} - \sqrt{m}}$ ，且 $a + b + 3 a b = 2021$ ，求 $m$ 的值．

(3)、已知 $\sqrt{15 + x^{2}} - \sqrt{26 - x^{2}} = 1$ ，求 $\sqrt{15 + x^{2}} + \sqrt{26 - x^{2}}$ 的值．

查看试题解析

湘教版数学八年级上册《 第5章 二次根式》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共10题，共72分）

湘教版数学八年级上册《第5章二次根式》单元提升测试卷