浙教版数学八年级上册《第5章一次函数》单元提升测试卷

试卷更新日期：2024-08-13 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在平面直角坐标系中，一次函数y＝x+1的图象不经过的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 弹簧挂重物会伸长，测得弹簧长度y（cm）最长为20cm，与所挂物体重量x（kg）有下面的关系．

x

0

1

2

3

4

…

y

8

8.5

9

9.5

10

…

下列说法不正确的是（）

A、x与y都是变量，x是自变量，y是因变量 B、所挂物体为6kg，弹簧长度为11cm C、物体每增加1kg，弹簧长度就增加0.5cm D、挂30kg物体时一定比原长增加15cm

查看试题解析
3. 匀速地向如图所示的容器内注水，直到把容器注满．在注水过程中，容器内水面高度h随时间t变化的大致图象是（　　）

A、 B、 C、 D、

查看试题解析
4. 如图1“燕几”即宴几，是世界上最早的一套组合桌，由北宋进士黄伯思设计.全套“燕几”一共有七张桌子，包括两张长桌、两张中桌和三张小桌，每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图2给出了《燕几图》中名称为“回文”的桌面拼合方式，若设每张桌面的宽为 $x$ 尺，长桌的长为 $y$ 尺，则 $y$ 与 $x$ 的关系可以表示为（）

A、 $y = 3 x$ B、 $y = 4 x$ C、 $y = 3 x + 1$ D、 $y = 4 x + 1$

查看试题解析
5. 已知一次函数y=kx+b（k≠0）图象过点（0，2），且与两坐标轴围成的三角形面积为2，则一次函数的解析式为（）

A、y= x+2 B、y= ﹣x+2 C、y= x+2或y=﹣x+2 D、y= - x+2或y = x-2

查看试题解析
6. 如图，直线AB对应的函数表达式是（）

A、y= $- \frac{3}{2}$ x+2 B、y= $\frac{3}{2}$ x+3 C、y= $- \frac{2}{3}$ x+2 D、y= $\frac{2}{3}$ x+2

查看试题解析
7. 如图，在同一平面直角坐标系中，一次函数 $y = k_{1} x + b_{1}$ 与 $y = k_{2} x + b_{2}$ （其中 $k_{1} k_{2} \neq 0$ ， $k_{1}$ ， $k_{2}$ ， $b_{1}$ ， $b_{2}$ 为常数）的图象分别为直线 $l_{1}$ ， $l_{2}$ .下列结论正确的是（）

A、 $b_{1} + b_{2} > 0$ B、 $b_{1} b_{2} > 0$ C、 $k_{1} + k_{2} < 0$ D、 $k_{1} k_{2} < 0$

查看试题解析
8. 在同一平面直角坐标系中，一次函数 $y_{1} = a x + b (a \neq 0)$ 与 $y_{2} = m x + n (m \neq 0)$ 的图象如图所示，则（）

A、当 $x > 2$ 时， $y_{1} < y_{2}$ B、当 $x < 0$ 时， $y_{1} > 3, y_{2} < 3$ C、 $b - n = 2 (m - a)$ D、关于x，y的方程组 ${\begin{array}{l} a x - y = - b \\ m x - y = - n \end{array}$ 的解为 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$

查看试题解析
9. 已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是：该同学从家跑步去体育场，在那里锻炼了一阵后又步行回家吃早餐，饭后骑自行车到图书馆.图中用x表示时间，y表示该同学离家的距离.结合图象给出下列结论：
①体育场离该同学家2.5千米；
②该同学在体育场锻炼了15分钟；
③该同学跑步前平均速度是步行平均速度的2倍；
④若该同学骑行的平均速度是跑步平均速度的1.5倍，则 $a$ 的值是3.75；
其中正确结论的个数是( )

A、1 B、2 C、3 D、4

查看试题解析
10. 甲从深圳匀速骑电动车到广州，乙从广州匀速骑摩托车到深圳，两人同时出发，到达目的地后，立即停止运动，甲、乙两人离深圳的距离 $y (k m)$ 与他们骑车的时间 $x (h)$ 之间的函数关系如图所示，则下列说法错误的是（）

A、深广两地的距离为 $120 k m$ B、甲的速度为 $20 k m / h$ C、乙的速度为 $30 k m / h$ D、乙运动 $3 h$ 到达深圳

查看试题解析

二、填空题（每题3分，共18分）

11. 已知一次函数y=kx+b的图象经过点（1，3），（-1，2），则k²-b²=.

查看试题解析

12. 每年夏季的7月份和8月份，运城市盐湖区迎来高温天气，居民家中一般采用开空调的方式降温，家中的用电量也剧增，下表是山西省一户一表的居民用户电价表，每月的用电量如果是小数，四舍五入取整．运城市盐湖区某小区都是一户一表居民用户，若住在此小区的某户居民2023年7月和8月双月用电总量为x度

(x > 521)

，费用y元，则y与x之间的关系式为．

	山西省居民电价表
用户分类	分档	电量（度）	电价（元/度）	执行周期
一户一表居民用户	第一档	$0 - 340$ （双月电量340度及以内）	0.477	居民阶梯电价以“双月”为周期执行
	第二档	$341 - 520$ （双月电量超过340度但不超过520度）	0.527
	第三档	521及以上（双月电量521度及以上）	0.777

查看试题解析

13. 甲、乙两个工程组同时挖掘沈白高铁某段隧道，两组每天挖掘长度均保持不变，合作一段时间后，乙组因维修设备而停工，甲组单独完成了剩下的任务，甲、乙两组挖掘的长度之和 $y (m)$ 与甲组挖掘时间x（天）之间的关系如图所示．则乙组每天挖掘m.

查看试题解析
14. 如图，函数y＝﹣3x和y＝kx+b的图象交于点A（m，4），则关于x的不等式（k+3）x+b＜0的解集为．

查看试题解析
15. 一个装有进水管和出水管的容器，开始时，先打开进水管注水，3分钟时，再打开出水管排水，8分钟时，关闭进水管，直至容器中的水全部排完.在整个过程中，容器中的水量y（升）与时间x（分钟）之间的函数关系如图所示，则图中a的值为.

查看试题解析
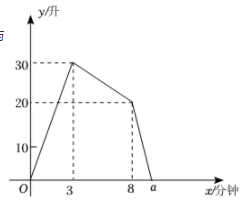16. 甲地宏达物流公司的快递车和货车同时从甲地出发，以各自的速度沿快速通道向乙地匀速行驶，快递车到达乙地后，卸完物资并另装货物共用了 $45$ 分钟，然后按原路以另一速度返回，直至与货车相遇，已知货车行驶速度为 $60 k m / h$ ，两车间的距离 $y (k m)$ 与货车行驶时间 $x (h)$ 之间的函数图象如图所示
给出以下四个结论：
①快递车从甲地到乙地的速度是 $100 k m / h$
②甲、乙两地之间的距离是 $80 k m$
③图中点 $B$ 的坐标为 $(2 \frac{3}{4} ， 35)$
④快递车从乙地返回时的速度为 $90 k m / h$
其中正确的是 $($ 填序号 $)$

查看试题解析

三、解答题（共8题，共72分）

17. 如图是1个碗和4个整齐叠放成一摞的碗的示意图，碗的规格都是相同的．小亮尝试结合学习函数的经验，探究整齐叠放成一摞的这种规格的碗的总高度y（单位：cm）随着碗的数量x（单位：个）的变化规律．下表是小亮经过测量得到的y与x之间的对应数据：
x/个
1
2
3
4
y/cm
6
8.4
10.8
13.2

(1)、依据小亮测量的数据，写出y与x之间的函数表达式，并说明理由；

(2)、若整齐叠放成一摞的这种规格的碗的总高度不超过28.8cm ，求此时碗的数量最多为多少个？

查看试题解析
18. 已知小华同学的家离学校 $1000 m$ ．根据以往经验，小华在平面直角坐标系中绘制了在学校和家之间的路上匀速行走时小华和小华妈妈离学校的距离 $y$ （单位： $m$ ）和出发的时间 $x$ （单位： $m i n$ ）的函数图象，分别如图中的线段OA，BC.

(1)、分别求出小华和小华妈妈步行的速度v₁和v₂；

(2)、一天放学后，小华从学校往家的方向行走，小华妈妈也同时从家里出发步行往学校方向走，两人汇合一同去参加一个志愿者活动，求小华和小华妈妈多少 $m i n$ 能汇合．

查看试题解析
19. 如图，在直角坐标系中，点 $A (2, m)$ 在直线 $y = 2 x - \frac{5}{2}$ 上，过点A的直线交y轴于点 $B (0, 3)$ ．

(1)、求m的值和直线的函数表达式．

(2)、若点 $P (t, y_{1})$ 在线段AB上，点 $Q (t - 2, y_{2})$ 在直线 $y = 2 x - \frac{5}{2}$ 上，求 $y_{1} - y_{2}$ 的最小值．

查看试题解析
20. 如图，在平面直角坐标系中，点 $A (- 2 m)$ 在直线 $y = - 2 x - 1$ 上，过点 $A$ 的直线交 $y$ 轴于点B $(0, 5)$ .

(1)、求 $m$ 的值和直线 $A B$ 的函数表达式.

(2)、若点 $P (t, y_{1})$ 在直线AB上，点 $Q (t - 1, y_{2})$ 在直线 $y = - 2 x - 1$ 上，当 $t$ 取任意实数时，代数式 $y_{1} + k y_{2}$ 的值为定值，求 $k$ 的值，并求出这个定值.

查看试题解析
21. 为了解某新能源汽车的充电速度，某数学兴趣小组经研究发现：如图，用快速充电器时，汽车电池电量 $y_{1} ($ 单位： $%)$ 与充电时间 $x ($ 单位： $h)$ 的函数图象是折线 $A B C$ ；用普通充电器时，汽车电池电量 $y_{2} ($ 单位： $%)$ 与充电时间 $x ($ 单位： $h)$ 的函数图象是线段 $A D .$
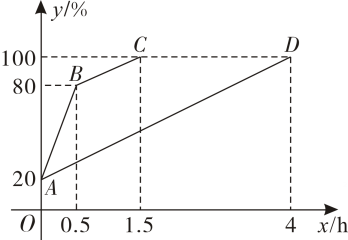
根据以上信息，回答下列问题：

(1)、普通充电器对该汽车每小时的充电量为 $%$ ；

(2)、求 $y_{1}$ 与 $x$ 的函数解析式，并写出 $x$ 的取值范围；

(3)、若将该汽车电池电量从 $20 %$ 充至 $90 %$ ，快速充电器比普通充电器少用 $h .$

查看试题解析
22. 共享电动车是一种新理念下的交通工具：主要面向 $3$ ～ $10 k m$ 的出行距离．现有 $A$ 、 $B$ 两种品牌的共享电动车，收费与骑行时间之间的函数关系如图所示，其中 $A$ 品牌收费方式对应 $y_{1}$ ， $B$ 品牌的收费方式对应 $y_{2}$ ．

(1)、 $A$ 品牌每分钟收费元；

(2)、求 $B$ 品牌的函数关系式；

(3)、如果小明每天早上需要骑行 $A$ 品牌或 $B$ 品牌的共享电动车去工厂上班，已知两种品牌共享电动车的平均行驶速度均为 $20 k m / h$ ，小明家到工厂的距离为 $6 k m$ ，那么小明选择哪个品牌的共享电动车更省钱呢？

查看试题解析
23. 综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究．第一小组负责调查板凳的历史及结构特点；第二小组负责研究板凳中蕴含的数学知识；第三小组负责汇报和交流．下面是第三小组汇报的部分内容，请你阅读相关信息，并解答“建立模型”中的问题．
【背景调查】
图①中的板凳又叫“四脚八叉凳”，是中国传统家具，其榫卯结构体现了古人含蓄内敛的审美观．榫眼的设计很有讲究，木工一般用铅笔画出凳面的对称轴，以对称轴为基准向两边各取相同的长度，确定榫眼的位置，如图②所示．板凳的结构设计体现了数学的对称美．
【收集数据】
小组收集了一些板凳并进行了测量．设以对称轴为基准向两边各取相同的长度为x mm ，凳面的宽度为y mm ，记录如下：
以对称轴为基准向两边各取相同的长度x/mm
16.5
19.8
23.1
26.4
29.7
凳面的宽度y/mm
115.5
132
148.5
165
181.5
【分析数据】
如图③，小组根据表中x ， y的数值，在平面直角坐标系中描出了各点．
【建立模型】
请你帮助小组解决下列问题：

(1)、观察上述各点的分布规律，它们是否在同一条直线上？如果在同一条直线上，求出这条直线所对应的函数解析式；如果不在同一条直线上，说明理由．

(2)、当凳面宽度为213mm时，以对称轴为基准向两边各取相同的长度是多少？

查看试题解析
24. 如图，直线 $y = k x + 6$ 与 $x$ 轴分别交于 $E$ ， $F$ ，点 $E$ 坐标为 $(- 8 ， 0)$ ，点 $A$ 的坐标为 $(- 6 ， 0)$ ， $P (x$ ， $y)$ 是直线 $y = k x + 6$ 上的一个动点．

(1)、求 $k$ 的值；

(2)、当点 $P$ 在第二象限内运动过程中，试写出三角形 $O P A$ 的面积 $s$ 与 $x$ 的函数关系式，并写出自变量 $x$ 的取值范围；

(3)、探究：当 $P$ 运动到什么位置时，三角形 $O P A$ 的面积为 $\frac{27}{8}$ ，并说明理由．

查看试题解析

以对称轴为基准向两边各取相同的长度x/mm	16.5	19.8	23.1	26.4	29.7
凳面的宽度y/mm	115.5	132	148.5	165	181.5

x	0	1	2	3	4	…
y	8	8.5	9	9.5	10	…

x/个	1	2	3	4
y/cm	6	8.4	10.8	13.2

浙教版数学八年级上册《 第5章 一次函数》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

浙教版数学八年级上册《第5章一次函数》单元提升测试卷