北师大版数学九年级上册《第五章 投影与视图》单元提升测试卷
试卷更新日期:2024-08-13 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 马家窑彩陶绚丽典雅,符号丰富,被称为彩陶文化的“远古之光”.如图是一件马家窑彩陶作品的立体图形,有关其三视图说法正确的是( )
 A、主视图和左视图完全相同 B、主视图和俯视图完全相同 C、左视图和俯视图完全相同 D、三视图各不相同2. 由四个相同的小立方体拼成的几何体如图所示, 当光线由上向下垂直照射时, 该几何体在水平投影面上的正投影是( )
A、主视图和左视图完全相同 B、主视图和俯视图完全相同 C、左视图和俯视图完全相同 D、三视图各不相同2. 由四个相同的小立方体拼成的几何体如图所示, 当光线由上向下垂直照射时, 该几何体在水平投影面上的正投影是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为( )
3. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为( ) A、3m B、4m C、4.5m D、5m4. 如图,有一路灯杆AP,路灯P距地面4.8m,身高1.6m的小明站在距A点4.8m的点D处,小明的影子为DE,他沿射线DA走2.4m到达点B处,小明的影子为BC,此时小明影子的长度( )
A、3m B、4m C、4.5m D、5m4. 如图,有一路灯杆AP,路灯P距地面4.8m,身高1.6m的小明站在距A点4.8m的点D处,小明的影子为DE,他沿射线DA走2.4m到达点B处,小明的影子为BC,此时小明影子的长度( ) A、增长了1m B、缩短了1m C、增长了1.2m D、缩短了1.2m5. 如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是( )
A、增长了1m B、缩短了1m C、增长了1.2m D、缩短了1.2m5. 如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是( ) A、①②③④ B、④③①② C、④①③② D、②①③④6. 如图所示,在房子的屋檐处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区( )
A、①②③④ B、④③①② C、④①③② D、②①③④6. 如图所示,在房子的屋檐处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区( ) A、△ACE B、△ADF C、△ABD D、四边形BCED7. 某几何体由若干个大小相同的小正方体组成,其主视图、左视图和俯视图都如图所示.则组成该几何体的小正方体的个数最少为( )
A、△ACE B、△ADF C、△ABD D、四边形BCED7. 某几何体由若干个大小相同的小正方体组成,其主视图、左视图和俯视图都如图所示.则组成该几何体的小正方体的个数最少为( ) A、4个 B、6个 C、7个 D、3个8. 如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
A、4个 B、6个 C、7个 D、3个8. 如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )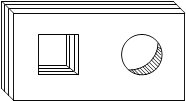 A、
A、 B、
B、 C、
C、 D、
D、 9. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
9. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )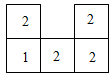 A、3 B、4 C、6 D、910. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、3
A、3 B、4 C、6 D、910. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、3二、填空题(每题3分,共18分)
-
11. 《孙子算经》是我国古代重要的数学著作,其有题译文如下:“有一根竹竿在太阳下的影子长15尺.同时立一根1.5尺的小标杆,它的影长是0.5尺.如图所示,则可求得这根竹竿的长度为尺.
 12. 一个正三棱柱的三视图如图所示,若这个正三棱柱的表面积为24+8 , 则a的值是 .
12. 一个正三棱柱的三视图如图所示,若这个正三棱柱的表面积为24+8 , 则a的值是 .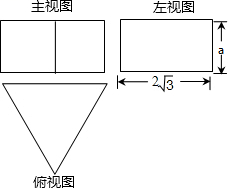 13. 如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为 , 则木杆在轴上的影长为 .
13. 如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为 , 则木杆在轴上的影长为 . 14. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为m.
14. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为m.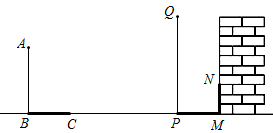 15. 如图,物体在灯泡发出的光照射下形成的影子是投影.(填“平行”或“中心”).
15. 如图,物体在灯泡发出的光照射下形成的影子是投影.(填“平行”或“中心”). 16. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.
16. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.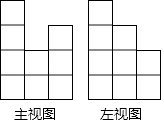
三、解答题(共8题,共72分)
-
17. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关因此,他们认为:可以借助物体的影子长度计算光源到物体的位置于是,他们做了以下尝试.
 (1)、如图 , 垂直于地面放置的正方形框架 , 边长为 , 在其上方点处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为那么灯泡离地面的高度为多少.(2)、不改变图中灯泡的高度,将两个边长为的正方形框架按图摆放,请计算此时横向影子 , 的长度和为多少?18. 由若干个棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的小正方体个数.
(1)、如图 , 垂直于地面放置的正方形框架 , 边长为 , 在其上方点处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为那么灯泡离地面的高度为多少.(2)、不改变图中灯泡的高度,将两个边长为的正方形框架按图摆放,请计算此时横向影子 , 的长度和为多少?18. 由若干个棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的小正方体个数. (1)、请画出它的主视图和左视图;(2)、如果要给这个几何体喷上颜色(底面不喷色),需要喷色的面积为;(3)、在不改变主视图和俯视图的情况下,最多可添加个小正方体.19. 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点B处时,李明直立时身高的影子恰好是线段 , 并测得 , 已知李明直立时的身高为 , 求路灯的高的长.(结果精确到.
(1)、请画出它的主视图和左视图;(2)、如果要给这个几何体喷上颜色(底面不喷色),需要喷色的面积为;(3)、在不改变主视图和俯视图的情况下,最多可添加个小正方体.19. 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点B处时,李明直立时身高的影子恰好是线段 , 并测得 , 已知李明直立时的身高为 , 求路灯的高的长.(结果精确到.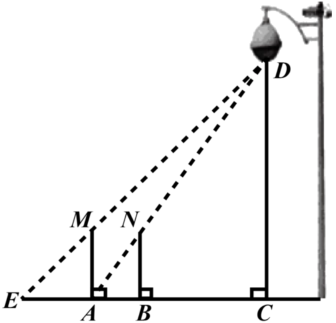 20. 如图,小树AB在路灯O的照射下形成投影BC .
20. 如图,小树AB在路灯O的照射下形成投影BC . (1)、此光源下形成的投影属于 . (填“平行投影”或“中心投影”)(2)、已知树高AB为2m,树影BC为3m,树与路灯的水平距离BP为4.5m.求路灯的高度OP .21. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)、此光源下形成的投影属于 . (填“平行投影”或“中心投影”)(2)、已知树高AB为2m,树影BC为3m,树与路灯的水平距离BP为4.5m.求路灯的高度OP .21. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.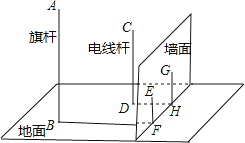 (1)、该小组的同学在这里利用的是 投影的有关知识进行计算的;(2)、试计算出电线杆的高度,并写出计算的过程。
(1)、该小组的同学在这里利用的是 投影的有关知识进行计算的;(2)、试计算出电线杆的高度,并写出计算的过程。
22. 如图,一路灯与墙相距20米,当身高米的小亮在离墙17米的D处时,影长为1米. (1)、求路灯B的高度;(2)、若点P为路灯,请画出小亮位于N处时,在路灯P下的影子NF(用粗线段表示出来)23. 小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)、求路灯B的高度;(2)、若点P为路灯,请画出小亮位于N处时,在路灯P下的影子NF(用粗线段表示出来)23. 小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答: (1)、如图1,白天在阳光下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .
(1)、如图1,白天在阳光下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .①若木杆 的长为 ,则其影子 的长为 ;
②在同一时刻同一地点,将另一根木杆 直立于地面,请画出表示此时木杆 在地面上影子的线段 ;
(2)、如图2,夜晚在路灯下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .①请在图中画出表示路灯灯泡位置的点 ;
②若木杆 的长为 ,经测量木杆 距离地面 ,其影子 的长为 ,则路灯 距离地面的高度为 .
24. 目标检测是一种计算机视觉技术,旨在检测汽车、建筑物和人类等目标.这些目标通常可以通过图像或视频来识别.在常规的目标检测任务中,如图1,一般使用边同轴平行的矩形框进行标示.在平面直角坐标系中,针对目标图形G,可以用其投影矩形来检测.图形G的投影矩形定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为k,我们称常数k为图形G的投影比.如图2,矩形为的投影矩形,其投影比 .

 (1)、如图3,点 , , 则投影比k的值为;(2)、如图4,若点 , 点且投影比 , 则点P的坐标可能是(填写序号);
(1)、如图3,点 , , 则投影比k的值为;(2)、如图4,若点 , 点且投影比 , 则点P的坐标可能是(填写序号);;;; .
(3)、如图5,已知点 , 在函数(其中)的图象上有一点D,若的投影比 , 求点D的坐标.