北师大版数学八年级上册《第六章 数据的分析》单元提升测试卷
试卷更新日期:2024-08-13 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 某文具超市有四种水笔销售,它们的单价分别是5元,4元,3元,1.2元.某天的水笔销售情况如图所示,那么这天该文具超市销售的水笔的单价的平均值是( )
 A、4元 B、4.5元 C、3.2元 D、3元2. 在年贵州某大学数学与统计学院的研究生入学考试中,三名考生甲、乙、丙在笔试、面试中的成绩百分制如下表所示,你觉得被录取的考生是( )
A、4元 B、4.5元 C、3.2元 D、3元2. 在年贵州某大学数学与统计学院的研究生入学考试中,三名考生甲、乙、丙在笔试、面试中的成绩百分制如下表所示,你觉得被录取的考生是( )考生
笔试
面试
甲
乙
丙
A、甲 B、乙 C、丙 D、无法判断3. 某商店销售种领口大小分别为 , , , , 单位:的衬衫,一个月内的销量如下表:领口大小
销量件
你认为商店最感兴趣的是这里数据的( )
A、平均数 B、中位数 C、众数 D、加权平均数4. 小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )A、方差 B、平均数 C、众数 D、中位数5. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,某校调查了一个班50名学生每天的睡眠时间,绘成睡眠时间条形统计图如图所示,则所调查学生睡眠时间的中位数为( ) A、6h B、7h C、7.5h D、8h6. 一组数据、、、、、、的平均数是 , 方差是 , 则另一组数据、、、、、、的平均数和方差分别是( )A、3, B、 , C、 , D、 ,7. 甲、乙两人在相同的条件下各射击10次,将每次命中的环数绘制成如图所示统计图.根据统计图得出的结论正确的是( )
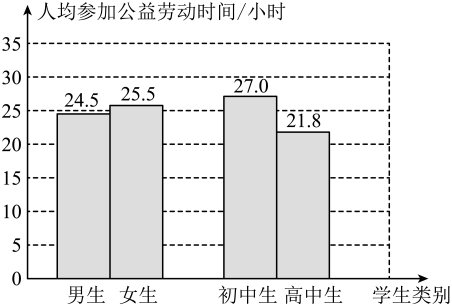
A、6h B、7h C、7.5h D、8h6. 一组数据、、、、、、的平均数是 , 方差是 , 则另一组数据、、、、、、的平均数和方差分别是( )A、3, B、 , C、 , D、 ,7. 甲、乙两人在相同的条件下各射击10次,将每次命中的环数绘制成如图所示统计图.根据统计图得出的结论正确的是( ) A、甲的射击成绩比乙的射击成绩更稳定 B、甲射击成绩的众数大于乙射击成绩的众数 C、甲射击成绩的平均数大于乙射击成绩的平均数 D、甲射击成绩的中位数大于乙射击成绩的中位数8. 如果样本方差S2= [(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2],则样本和x1+x2+x3+x4+x5= ( )A、10 B、4 C、5 D、29. 某篮球队5名场上队员的身高(单位: )分别是183、187、190、200、195,现用一名身高为 的队员换下场上身高为 的队员,与换人前相比,场上队员身高的( )A、平均数变大,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变大 D、平均数变小,方差变小10. 某校共有200名学生.为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据.下图是根据数据绘制的统计图表的一部分.下面有四个推断:
A、甲的射击成绩比乙的射击成绩更稳定 B、甲射击成绩的众数大于乙射击成绩的众数 C、甲射击成绩的平均数大于乙射击成绩的平均数 D、甲射击成绩的中位数大于乙射击成绩的中位数8. 如果样本方差S2= [(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2],则样本和x1+x2+x3+x4+x5= ( )A、10 B、4 C、5 D、29. 某篮球队5名场上队员的身高(单位: )分别是183、187、190、200、195,现用一名身高为 的队员换下场上身高为 的队员,与换人前相比,场上队员身高的( )A、平均数变大,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变大 D、平均数变小,方差变小10. 某校共有200名学生.为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据.下图是根据数据绘制的统计图表的一部分.下面有四个推断:①这200名学生参加公益劳动时间的平均数一定在 之间;②这200名学生参加公益劳动时间的中位数在 之间;③这200名学生中的初中生参加公益劳动时间的中位数一定在 之间;④这200名学生中的高中生参加公益劳动时间的中位数可能在 之间.
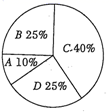
所有合理推断的序号是( )
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中
 A、①③ B、②④ C、①②③ D、①②③④
A、①③ B、②④ C、①②③ D、①②③④二、填空题(每题3分,共18分)
-
11. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,评价成绩80分以上(含80分)为“优秀”.下面表中是小王同学的成绩记录:
项目
完成作业
单元测试
期末考试
成绩
65
75
若完成作业、单元检测、期末考试三项成绩按1:3:6的权重来确定期末评价成绩,小王的期末评价为优秀,那么他的期末考试最低成绩是.
12. 在2015年的体育考试中某校6名学生的体育成绩统计如图所示,这组数据的中位数是 . 13. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:cm)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是 .
13. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:cm)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是 .甲
乙
丙
丁
平均数
376
350
376
350
方差
12.5
13.5
2.4
5.4
14. 若一组数据6,9,11,13,11,7,10,8,12的中位数是m,众数是n,则关于x,y的方程组 的解是.15. 现有两组数据:甲:12,14,16,18;乙:2023,2022,2020,2019,它们的方差分别记作 , , 则(用“>”“=”“<”).16. 某班四个学习兴趣小组的学生分布如图①②,现通过对四个小组学生寒假期间所读课外书情况进行调查,并制成各小组读书情况的条形统计图③,根据统计图中的信息:这四个小组平均每人读书的本数是本.


三、解答题(共8题,共72分)
-
17. 某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:)如下:
甲: 1. 71,1. 65,1. 68,1. 68,1. 72,1. 73,1. 68,1. 67;
乙: 1. 60,1. 74,1. 72,1. 69,1. 62,1. 71,1. 69,1. 75;
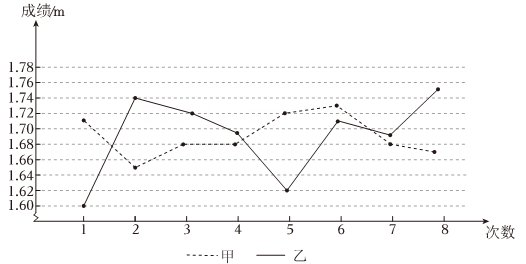 (1)、【整理与分析】
(1)、【整理与分析】平均数 众数 中位数 甲 1.69 a 1.68 乙 1.69 1.69 b
①由上表填空: , ;②这两人中,的成绩更为稳定。
(2)、【判断与决案】经预测,跳高就很可能获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员参赛?请说明理由。
18. 某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试.各项满分均为10分,平均成绩高者被录用.图1是甲、乙测试成绩的条形统计图, (1)、分别求出甲、乙三项平均成绩,并指出会录用谁;(2)、若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.19. 杭州亚运会开幕式惊艳了世界,这背后离不开志愿者们的默默奉献,这些志愿者很多都来自高校.在志愿者招募之时, , 两所大学就积极组织了志愿者选拔活动,对报名的志愿者进行现场测试,现从这两所大学参加测试的志愿者中分别随机抽取了20名志愿者的综合测试成绩进行整理和分析,下面给出部分信息.综合以上信息,解答下列问题:
(1)、分别求出甲、乙三项平均成绩,并指出会录用谁;(2)、若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.19. 杭州亚运会开幕式惊艳了世界,这背后离不开志愿者们的默默奉献,这些志愿者很多都来自高校.在志愿者招募之时, , 两所大学就积极组织了志愿者选拔活动,对报名的志愿者进行现场测试,现从这两所大学参加测试的志愿者中分别随机抽取了20名志愿者的综合测试成绩进行整理和分析,下面给出部分信息.综合以上信息,解答下列问题:
, 两所大学被抽取的志愿者测试成绩的平均分、中位数、众数如下表:
学校
平均分
中位数
众数
校
95
校
93.5
95
(1)、填空: , , ;(2)、校志愿者的成绩的扇形统计图中的圆心角 ▲ °,请补全校志愿者的成绩的条形统计图;(3)、如果你是组委会成员,你倾向招哪所大学的志愿者?请说明理由.20. 某校开展了以“追梦新时代”为主题的读书活动,并对本校八年级学生12月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示.

根据以上信息,解答下列问题;
(1)、求出随机被抽查的学生总数,并补全不完整的条形统计图;(2)、填写本次所抽取学生12月份“读书量”的中位数为 本,众数为 本;(3)、求本次所抽取学生12月份“读书量”的平均数.21. 某校组织了一次“校徽设计“竞赛活动,邀请名老师作为专业评委,名学生代表参与民主测评,且民主测评的结果无弃权票.某作品的评比数据统计如下:
专业评委
给分单位:分
专业评委给分统计表
记“专业评委给分”的平均数为 .
(1)、求该作品在民主测评中得到“不赞成”的票数;(2)、对于该作品,问的值是多少?(3)、记“民主测评得分”为 , “综合得分”为 , 若规定:“赞成”的票数分“不赞成”的票数分;
.
求该作品的“综合得分”的值.
22. 甲、乙两名队员参加射击选拔赛,他们两人10次射击训练的成绩情况如下:甲队员: ;
乙队员的成绩如下图:

根据以上信息,整理分析数据如下:
队员
平均数(环)
中位数(环)
众数(环)
方差(环2)
甲
7.9
4.09
乙
7
7
(1)、表格中 , , ;(2)、求出 的值,并判断哪名队员的成绩更稳定?(3)、若从甲、乙两名队员中选派其中一名队员参赛,你认为应选哪名队员?请结合表中的四个统计量,作出简要分析.23. 小彬在今年的篮球联赛中表现优异.下表是他在这场联赛中,分别与甲队和乙队各四场比赛中的技术统计.场次
对阵甲队
对阵乙队
得分
篮板
失误
得分
篮板
失误
第一场
21
10
2
25
17
2
第二场
29
10
2
31
15
0
第三场
24
14
3
16
12
4
第四场
26
10
5
22
8
2
平均值
11
2
23.5
13
2
(1)、小彬在对阵甲队时的平均每场得分的值是分;(2)、小彬在这8场比赛的篮板统计数据中,众数是 , 中位数是;(3)、如果规定“综合得分”为:平均每场得分平均每场篮板平均每场失损 , 且综合得分越高表现越好.利用这种方式,我可以计算得出小彬在对阵乙队时的“综合得分”是37.1分.请你比较小彬在对阵哪一个队时表现更好,并说明理由.24. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(Ⅰ)图1中a的值为 ▲ ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.