北师大版数学八年级上册《第六章数据的分析》单元同步测试卷

试卷更新日期：2024-08-13 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 小雨同学参加了学校举办的“向着中华民族的伟大复兴奋进”主题演讲比赛，她的演讲内容、语言表达和形象风度三项得分分别为80分，90分，85分，若这三项依次按照50%，30%，20%的百分比确定成绩，则她的成绩是(　　)

A、82分 B、83分 C、84分 D、85分

查看试题解析
2. 某射击队准备挑选运动员参加射击比赛，下表是其中一名运动员10次射击的成绩（单位：环），则该名运动员射击成绩的平均数是（）
成绩
8
8.5
9
10
频数
3
2
4
1

A、8.9 B、8.7 C、8.3 D、8.2

查看试题解析
3. 在 $2014$ 年 $5$ 月崇左市教育局举行的“经典诗朗诵”演讲比赛中，有 $11$ 名学生参加决赛．他们决赛的成绩各不相同，其中的一名学生想要知道自己能否进入前 $6$ 名，不仅要了解自己的成绩，还要了解这 $11$ 名学生成绩的（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
4. 某企业车间有 $20$ 名工人，某一天他们生产的机器零件个数统计如表：
零件个数（个）
6
7
8
人数（人）
9
8
3
表中表示零件个数的数据中，众数、中位数分别是（　　）

A、7个，7个 B、6个，7个 C、 $12$ 个， $12$ 个 D、8个，6个

查看试题解析
5. 在我市开展的“好书伴我成长”读书活动中，某中学为了解八年级300名学生读书情况，随机调查了八年级50名学生读书的册数，统计数据如下表所示：
册数
0
1
2
3
4
人数
3
13
16
17
1
那么这50名同学读书册数的众数，中位数分别是（　　）

A、3，2 B、3，3 C、2，3 D、3，1

查看试题解析
6. 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数 $\bar{x}$ （单位：环）及方差S²（单位：环）如表所示：根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（　　）

甲
乙
丙
丁
$\bar{x}$
9
8
9
9
S²
1.8
0.6
5
0.6

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 比赛中，评分时经常要“去掉一个最高分，去掉一个最低分”，所剩数据与原数据比较不受影响的是（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析

8. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.4	8.1

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

9. 甲、乙两名射击运动员分别进行了相同次数的射击训练，如果将甲、乙两人射击环数的平均数分别记作 ${\bar{x}}_{甲}$ 和 ${\bar{x}}_{乙}$ ，方差分别记作 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ ，那么下列描述能说明甲运动员成绩较好且更稳定的是（）

A、 ${\bar{x}}_{甲} > {\bar{x}}_{乙}$ 且 $S_{甲}^{2} < S_{乙}^{2}$ B、 ${\bar{x}}_{甲} > {\bar{x}}_{乙}$ 且 $S_{甲}^{2} > S_{乙}^{2}$ C、 ${\bar{x}}_{甲} < {\bar{x}}_{乙}$ 且 $S_{甲}^{2} < S_{乙}^{2}$ D、 ${\bar{x}}_{甲} < {\bar{x}}_{乙}$ 且 $S_{甲}^{2} > S_{乙}^{2}$

查看试题解析
10. 甲、乙两班举行电脑汉字输入速度比赛，参赛学生每分钟输入汉字的个数经统计后的结果如表：
班级
参加人数
中位数
方差
平均数
甲
55
148
192
135
乙
55
151
110
135
某同学根据表中数据分析得出下列结论：
①甲、乙两班学生成绩的平均水平相同；
②乙班优秀的人数多于甲班优秀的人数；（每分钟输入汉字≥150个为优秀）；
③甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是（）

A、（1）（2）（3） B、（1）（2） C、（1）（3） D、（2）（3）

查看试题解析

二、填空题（每题3分，共18分）

11. 小明参加“传承经典，筑梦未来”主题演讲比赛，其演讲形象、演讲内容、演讲效果三项成绩分别是9分、8分、9分．若将演讲形象、演讲内容、演讲效果三项成绩按2：5：3确定最终成绩，则小明的最终比赛成绩是分．

查看试题解析
12. 已知一组数据3，7，9，10， $x$ ， 12的唯一众数是9，则这组数据的中位数是.

查看试题解析
13. 某校男子足球队的年龄分布如图所示，则根据图中信息可知这些队员年龄的中位数是岁.

查看试题解析
14. 人数相同的甲乙两班学生在同一次数学单元测试中，班级平均分和方差如下： $x_{甲} = x_{乙}$ ＝85，s_甲²＝25，s_乙²＝16，则成绩较为稳定的班级是．

查看试题解析
15. 已知：一组数据 2、4、a、6、3 的平均数是 4 ，则这组数据的方差是.

查看试题解析
16. 甲、乙俩射击运动员进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9，乙的成绩如图所示.则甲、乙射击成绩的方差之间关系是（填“＜”，“=”，“＞”）.

查看试题解析

三、解答题（共8题，共72分）

17. 某校八年级学生在一次射击训练中，随机抽取10名学生的成绩如下表，请回答问题：
环数
6
7
8
9
人数
1
5
3
$m$

(1)、填空：10名学生的射击成绩的众数是，中位数是， $m =$ ；

(2)、求这10名学生的平均成绩；

查看试题解析
18. 本学期初，某校为迎接中华人民共和国成立七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代“为主题的读书活动．德育处对八年级学生九月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，绘制了两幅不完整的统计图（如图所示）．

(1)、请补全两幅统计图；本次所抽取学生九月份“读书量“的众数是多少；

(2)、求本次所抽取学生九月份“读书量”的平均数；

(3)、已知该校八年级有500名学生，请你估计该校八年级学生中，九月份“读书量“为5本的学生人数．

查看试题解析
19. 某校举办国学知识竞赛，设定满分10分，学生得分均为整数.在初赛中，甲、乙两组（每组10人）学生成绩如下（单位：分）
甲组：5，6，6，6，6，6，7，9，9，10.
乙组：5，6，6，6，7，7，7，7，9，10.
组别
平均数
中位数
众数
方差
甲组
7
$a$
6
2.6
乙组
$b$
7
$c$
${S_{乙}}^{2}$

(1)、以上成绩统计分析表中 $a =$ ， $b =$ ， $c =$ ；

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中属中游略偏上!”观察上面表格判断，小明可能是组的学生；

(3)、从平均数和方差看，若从甲、乙两组学生中选择一个成绩较为稳定的小组参加决赛，应选哪个组？并说明理由.

查看试题解析
20. 某校为培养学生的数学思维，激发学生的学习兴趣，开展了学生数学说题比赛，八年级（1）班和八年级（2）班各选出5位选手参赛，成绩（满分为100分）如下：
八（1）班：82，88，90，75，90；
八（2）班：78，95，85，82，85．
数据整理分析如下：

平均分
中位数
众数
方差
八（1）班
85
88
$b$
$c$
八（2）班
$a$
85
85
$31.6$

(1)、表中 $a =$ _▲_， $b =$ _▲_，求出方差 $c$ 的值；

(2)、你认为选哪个班代表八年级参加学校的决赛比较好，说明理由．（参考信息： $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ⋯ ⋯ + {(x_{n} - \bar{x})}^{2}]$ ）

查看试题解析
21. 某校八年级260名学生开展“好书伴成长”读书活动，要求每人每学期至少阅读4~7本课外读物，学期结束后随机抽查了若干名学生每人阅读课外书的数量，并分为四种类型， $A$ ：4本； $B$ ：5本； $C$ ：6本； $D$ ：7本，将各类的人数绘制成如图所示的扇形统计图和条形统计图.
图1 图2

(1)、求这次被调查学生的人数；

(2)、写出被调查学生每人阅读课外书数量的众数、中位数；

(3)、求被调查学生每人阅读课外书数量的平均数，并估计这260名学生阅读课外书的总数.

查看试题解析
22. 为了解学生的课外阅读情况，某语文教师随机抽取两个学生10天的课外阅读时间（分），记录如下：
刘军
30
37
45
35
36
60
42
42
55
42
方雯
38
40
35
36
35
37
40
40
55
36
整理上述数据制成如下图表：

平均数
中位数
众数
方差
刘军
a
42
c
$63.8$
方雯
$39.2$
b
40
$31.36$

(1)、直接写出方雯课外阅读时间的中位数 $b =$ ，刘军课外阅读时间的众数 $c =$ ．

(2)、求出刘军课外阅读时间的平均数 $a$ 的值；

(3)、如果每天课外阅读时间达40分钟计为达标，请你选择一统计量，说明哪个学生课外阅读达标．

查看试题解析
23. “99公益日”是一年一度的全民公益活动日，学校组织学生参加慈善捐款活动，为了解学生捐款情况，随机调查了该校的部分学生，根据调查结果，绘制了如下的统计图1和图2．请根据相关信息，解答下列问题：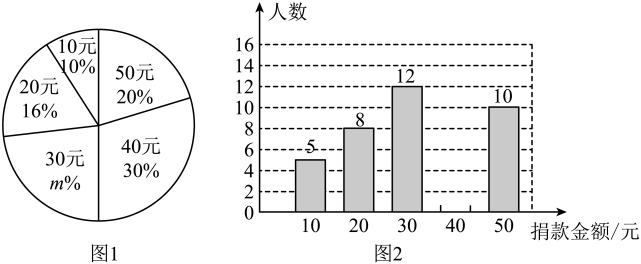

(1)、本次接受调查的学生人数为，图1中m的值为．

(2)、求统计的这组学生的捐款数据的平均数、众数和中位数．

(3)、根据统计的这组学生所捐款的情况，若该校共有1000名学生，估计该校共筹得善款多少元？

查看试题解析
24. 某学校七、八年级各有学生300人，为了普及冬奥知识，学校在七、八年级举行了一次冬奥知识竞赛，为了解这两个年级学生的冬奥知识竞赛成绩（百分制），分别从两个年级各随机抽取了20名学生的成绩，进行整理、描述和分析.下面给出了部分信息.
a.七、八年级成绩分布如下：
成绩 $x$ 年级
$0 \leq x$ $\leq 9$
$10 \leq x$ $\leq 19$
$20 \leq x$ $\leq 29$
$30 \leq x$ $\leq 39$
$40 \leq x$ $\leq 49$
$50 \leq x$ $\leq 59$
$60 \leq x$ $\leq 69$
$70 \leq x$ $\leq 79$
$80 \leq x$ $\leq 89$
$90 \leq x$ $\leq 100$
七
1
1
0
0
0
4
6
5
2
1
八
0
0
0
0
4
3
7
4
2
0
（说明：成绩在50分以下为不合格，在50～69分为合格，70分及以上为优秀）
b.八年级成绩在 $60 ～ 69$ 一组的是：61，62，63，65，66，68，69
c.七、八年级成绩的平均数中位数优秀率合格率如下：
年级
平均数
中位数
优秀率
合格率
七
$63 ． 3$
67
$n$
$90 %$
八
$64 ． 7$
$m$
$30 %$
$80 %$
根据以上信息，回答下列问题：

(1)、写出表中m，n的值；

(2)、小军的成绩在此次抽样之中，与他所在年级的抽样相比，小军的成绩高于平均数，却排在了后十名，则小军是年级的学生（填“七”或“八”）；

(3)、可以推断出年级的竞赛成绩更好，理由是（至少从两个不同的角度说明）.

查看试题解析

班级	参加人数	中位数	方差	平均数
甲	55	148	192	135
乙	55	151	110	135

组别	平均数	中位数	众数	方差
甲组	7	$a$	6	2.6
乙组	$b$	7	$c$	${S_{乙}}^{2}$

	平均分	中位数	众数	方差
八（1）班	85	88	$b$	$c$
八（2）班	$a$	85	85	$31.6$

成绩 $x$ 年级	$0 \leq x$ $\leq 9$	$10 \leq x$ $\leq 19$	$20 \leq x$ $\leq 29$	$30 \leq x$ $\leq 39$	$40 \leq x$ $\leq 49$	$50 \leq x$ $\leq 59$	$60 \leq x$ $\leq 69$	$70 \leq x$ $\leq 79$	$80 \leq x$ $\leq 89$	$90 \leq x$ $\leq 100$
七	1	1	0	0	0	4	6	5	2	1
八	0	0	0	0	4	3	7	4	2	0

年级	平均数	中位数	优秀率	合格率
七	$63 ． 3$	67	$n$	$90 %$
八	$64 ． 7$	$m$	$30 %$	$80 %$

成绩	8	8.5	9	10
频数	3	2	4	1

零件个数（个）	6	7	8
人数（人）	9	8	3

册数	0	1	2	3	4
人数	3	13	16	17	1

	甲	乙	丙	丁
$\bar{x}$	9	8	9	9
S²	1.8	0.6	5	0.6

北师大版数学八年级上册《第六章 数据的分析》单元同步测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学八年级上册《第六章数据的分析》单元同步测试卷