北师大版数学八年级上册《第五章 二元一次方程组》单元提升测试卷
试卷更新日期:2024-08-13 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 已知关于x、y的方程组 ,解是 ,则2m+n的值为( )A、﹣6 B、2 C、1 D、02. 在关于x,y的二元一次方程组中,若2x+3y=2,则a的值为( )A、2 B、3 C、4 D、-33. 若二元一次联立方程式的解为 , 则a+b之值为何?( )A、﹣28 B、﹣14 C、﹣4 D、144. 已知关于x , y的方程组 有以下结论:①当k=0时,方程组的解是;②当x+2y=0,则k=3;③不论k取什么实数,x+y的值始终不变.其中正确的是( )A、①② B、①③ C、②③ D、①②③5. 用白铁皮做罐头盒,每张铁皮可制盒身个,或制盒底个,一个盒身与两个盒底配成一套罐头盒,现有张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?设用张制盒身,张制盒底.根据题意可列出的方程组是( )A、 B、 C、 D、6. 用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
 A、200 B、201 C、202 D、2037. 一道来自课本的习题:
A、200 B、201 C、202 D、2037. 一道来自课本的习题:从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程 ,则另一个方程正确的是( )
A、 B、 C、 D、8. 一次函数与的图象如图所示,则下列说法不正确的是( )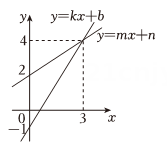 A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到39. 如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是( )
A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到39. 如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是( ) A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+610. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论:
A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+610. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论: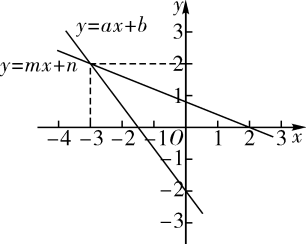
①在一次函数的图象中,的值随着值的增大而增大;②方程组的解为;③方程的解为;④当时,.
其中结论正确的个数是( )
A、1 B、2 C、3 D、4二、填空题(每题3分,共18分)
-
11. 已知关于 、 的二元一次方程组 的解是 ,则一次函数 和 的图象交点坐标为.12. 已知关于x , y的方程组的解的和是 , 则.13. 如图,10块相同的长方形卡片拼成一个大长方形,设长方形卡片的长和宽分别为x和y , 则依题意,列方程组 .
 14. 已知关于x,y的二元一次方程组 的解为 ,则关于m,n的二元一次方程组 的解为 .15. 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是cm.
14. 已知关于x,y的二元一次方程组 的解为 ,则关于m,n的二元一次方程组 的解为 .15. 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是cm.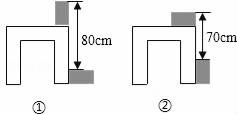 16. A、B、C三地在16同题一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时)y与x的关系如图所示,则B、C两地相距千米。
16. A、B、C三地在16同题一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时)y与x的关系如图所示,则B、C两地相距千米。
三、解答题(共7题,共72分)
-
17. 解方程组:(1)、;(2)、 .18. 解下列方程组:(1)、;(2)、 .19. 电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费(元)与用电量(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
 (1)、分别求出当和时,与的函数关系式.(2)、若该用户某月用了72度电,则应缴费多少元?(3)、若该用户某月缴费105元时,则该用户该月用了多少度电?20. 直线分别与轴交于两点,过点的直线交轴轴负半轴于 , 且 .
(1)、分别求出当和时,与的函数关系式.(2)、若该用户某月用了72度电,则应缴费多少元?(3)、若该用户某月缴费105元时,则该用户该月用了多少度电?20. 直线分别与轴交于两点,过点的直线交轴轴负半轴于 , 且 .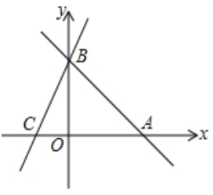 (1)、求点的坐标为;(2)、求直线的解析式;(3)、动点从出发沿射线方向运动,运动的速度为每秒1个单位长度.设运动秒时,当为何值时为等腰三角形.21. 第19届亚运于2023年9月23日至10月8日在杭州举行.某玩具店购进亚运会吉祥物“琮琮”、“莲莲”共100个,总费用为6600元,这两种吉祥物的进价、售价如表:
(1)、求点的坐标为;(2)、求直线的解析式;(3)、动点从出发沿射线方向运动,运动的速度为每秒1个单位长度.设运动秒时,当为何值时为等腰三角形.21. 第19届亚运于2023年9月23日至10月8日在杭州举行.某玩具店购进亚运会吉祥物“琮琮”、“莲莲”共100个,总费用为6600元,这两种吉祥物的进价、售价如表:
琮琮
莲莲
进价(元/个)
60
70
售价(元/个)
80
100
(1)、该玩具店购进“琮琮”和“莲莲”各多少个?(2)、后来该玩具店以60元/个的价格购进50个吉祥物“宸宸”,并以90元/个的价格售出,这家店将销售完这150个吉祥物所得利润的20%捐赠给了“希望工程”,求该玩具店捐赠了多少元?22. 阅读材料并回答下列问题:当 , 都是实数,且满足 , 就称点为“郡麓点”例如:点 , 令得 , , 所以不是“郡麓点”; , 令得 , , 所以是“郡麓点”.
(1)、请判断点 , 是否为“郡麓点”:(2)、若以关于 , 的方程组的解为坐标的点是“郡麓点”,求的值;(3)、若以关于 , 的方程组的解为坐标的点是“郡麓点”,求正整数 , 的值.23. 如图,已知直线与x轴、y轴分别交于两点,直线与y轴交于点C,与直线交于点D. (1)、求直线的表达式;(2)、点P是线段上一点,连接 , 当的面积为9,求P点坐标;(3)、若正比例函数的图象与直线交于点P,且点O、点P到直线的距离相等,请直接写出符合条件的m的值.
(1)、求直线的表达式;(2)、点P是线段上一点,连接 , 当的面积为9,求P点坐标;(3)、若正比例函数的图象与直线交于点P,且点O、点P到直线的距离相等,请直接写出符合条件的m的值.