北师大版数学八年级上册《第四章 一次函数》单元同步测试卷
试卷更新日期:2024-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图曲线中不能表示是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,小刚骑电动车到单位上班,最初以某一速度匀速行进,途中由于遇到火车挡道,停下等待放行,耽误了几分钟,为了按时到单位,小刚加快了速度,仍保持匀速行进,结果准时到单位.小刚行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,你认为正确的是( )A、
2. 如图,小刚骑电动车到单位上班,最初以某一速度匀速行进,途中由于遇到火车挡道,停下等待放行,耽误了几分钟,为了按时到单位,小刚加快了速度,仍保持匀速行进,结果准时到单位.小刚行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,你认为正确的是( )A、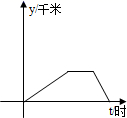 B、
B、 C、
C、 D、
D、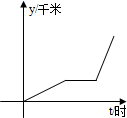 3. 下列4个函数关系:y=2x+1,y= ,s=60t,y=100﹣25x,其中是一次函数的共有( )A、1个 B、2个 C、3个 D、4个4. 甲、乙两地相距 , 一货车从甲地出发以的速度匀速向乙地行驶,则货车距离乙地的路程与时间之间的函数表达式是( )A、 B、 C、 D、5. 若函数是正比例函数,则的值是( )A、 B、 C、 D、6. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、7. 一次函数的图象是由的图象平移得到的,则移动方法为( )A、向右平移个单位 B、向左平移个单位 C、向上平移个单位 D、向下平移个单位8. 一次函数的图象如图所示,则值可能是( )
3. 下列4个函数关系:y=2x+1,y= ,s=60t,y=100﹣25x,其中是一次函数的共有( )A、1个 B、2个 C、3个 D、4个4. 甲、乙两地相距 , 一货车从甲地出发以的速度匀速向乙地行驶,则货车距离乙地的路程与时间之间的函数表达式是( )A、 B、 C、 D、5. 若函数是正比例函数,则的值是( )A、 B、 C、 D、6. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、7. 一次函数的图象是由的图象平移得到的,则移动方法为( )A、向右平移个单位 B、向左平移个单位 C、向上平移个单位 D、向下平移个单位8. 一次函数的图象如图所示,则值可能是( )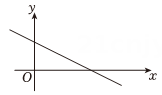 A、2 B、 C、 D、9. 已知一次函数 , 则该函数的图象大致是A、
A、2 B、 C、 D、9. 已知一次函数 , 则该函数的图象大致是A、 B、
B、 C、
C、 D、
D、 10. 已知(-3,y1),(1,y2),(-1,y3)都在直线y=3-b上,则下列关系式正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y1<y2
10. 已知(-3,y1),(1,y2),(-1,y3)都在直线y=3-b上,则下列关系式正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y1<y2二、填空题(每题3分,共18分)
-
11. 在平面直角坐标系中,一次函数y=+1的图象与y轴交点坐标为.12. 若一次函数是正比例函数,则的值为 .13. 某物体在力F的作用下,沿力的方向移动的距离为s,力对物体所做的功W与s的对应关系如图所示,则W与s之间的关系式是: .
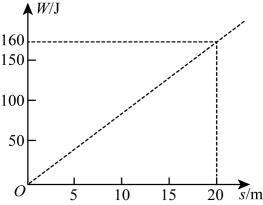 14. 已知关于x的一次函数y=mx+n的图象如图所示,则|n-m|-可化简为 .
14. 已知关于x的一次函数y=mx+n的图象如图所示,则|n-m|-可化简为 . 15. 在弹性限度内,弹簧的长度y cm与所挂物体的质量x kg之间是一次函数关系,其图象如图所示,则弹簧本身的长度为 .
15. 在弹性限度内,弹簧的长度y cm与所挂物体的质量x kg之间是一次函数关系,其图象如图所示,则弹簧本身的长度为 . 16. 直线y=﹣3x+b与直线y=2x+3的交点在y轴上,则b= .
16. 直线y=﹣3x+b与直线y=2x+3的交点在y轴上,则b= .三、解答题(共7题,共72分)
-
17. 已知关于x的函数y=(m-3)|m|-2+n-2(1)、当m,n为何值时它是一次函数?(2)、当m,n为何值时,它是正比例函数?18. 已知:一次函数 .(1)、若一次函数的图象过原点,求实数m的值;(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围;(3)、当一次函数的图象不经过第三象限时,求实数m的取值范围.19. 如图,直线与直线相交于点 .
 (1)、求b,m的值;(2)、垂直于x轴的直线交直线于C,D两点,若线段CD长为6,求点D的坐标.20. 一次函数 的图象经过点 和点 .
(1)、求b,m的值;(2)、垂直于x轴的直线交直线于C,D两点,若线段CD长为6,求点D的坐标.20. 一次函数 的图象经过点 和点 . (1)、求一次函数的表达式;(2)、若此一次函数的图象与 轴交于点 ,求 的面积.21. 如图,直线 : 与过点 的直线 交于点 .
(1)、求一次函数的表达式;(2)、若此一次函数的图象与 轴交于点 ,求 的面积.21. 如图,直线 : 与过点 的直线 交于点 .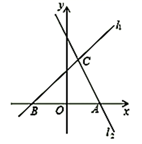 (1)、求m的值;(2)、求直线 的解析式.22. 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲 , y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)、求m的值;(2)、求直线 的解析式.22. 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲 , y乙与x之间的函数图象如图所示,结合图象解答下列问题: (1)、求:y甲与x的函数关系式,并写出自变量x的取值范围;(2)、乙车休息了h;(3)、当两车相距80km时,直接写出x的值.23. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
(1)、求:y甲与x的函数关系式,并写出自变量x的取值范围;(2)、乙车休息了h;(3)、当两车相距80km时,直接写出x的值.23. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:碗的数量(只) 1 2 3 4 5 ······ 高度(cm) 4 5.2 6.4 7.6 8.8 ······  (1)、上述两个变量之间的关系中,哪个是自变量?哪个是因变量?(2)、用h(cm)表示这摞碗的高度,用(只)表示这摞碗的数量,请用含有的代数式表示h;(3)、若这摞碗的高度为11.2cm,求这摞碗的数量.
(1)、上述两个变量之间的关系中,哪个是自变量?哪个是因变量?(2)、用h(cm)表示这摞碗的高度,用(只)表示这摞碗的数量,请用含有的代数式表示h;(3)、若这摞碗的高度为11.2cm,求这摞碗的数量.