北师大版数学八年级上册《第四章 一次函数》单元提升测试卷
试卷更新日期:2024-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列图象不能表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某品牌的自行车链条每节长为 , 每两节链条相连部分重叠的圆的直径为 , 按照这种连接方式,节链条总长度为 , 则与的关系式是( )
2. 某品牌的自行车链条每节长为 , 每两节链条相连部分重叠的圆的直径为 , 按照这种连接方式,节链条总长度为 , 则与的关系式是( ) A、 B、 C、 D、3. 若y=(k﹣2)x|k﹣1|+1表示一次函数,则k等于( )A、0 B、2 C、0或2 D、﹣2或04. 一次函数 满足 ,且y随x的增大而减小,则此函数的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A、
A、 B、 C、 D、3. 若y=(k﹣2)x|k﹣1|+1表示一次函数,则k等于( )A、0 B、2 C、0或2 D、﹣2或04. 一次函数 满足 ,且y随x的增大而减小,则此函数的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A、 B、
B、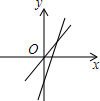 C、
C、 D、
D、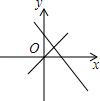 6. 若直线y=kx+b经过第一、二、四象限,则函数y=bx﹣k的大致图象是( )A、
6. 若直线y=kx+b经过第一、二、四象限,则函数y=bx﹣k的大致图象是( )A、 B、
B、 C、
C、 D、
D、 7. 关于一次函数 , 下列说法正确的是( )A、函数值随自变量的增大而减小 B、图象与轴交于点 C、点在函数图象上 D、图象经过第二、三、四象限8. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
7. 关于一次函数 , 下列说法正确的是( )A、函数值随自变量的增大而减小 B、图象与轴交于点 C、点在函数图象上 D、图象经过第二、三、四象限8. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t= 或 .
其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个9. 已知 , , 是直线为常数)上的三个点,则 , , 的大小关系是A、 B、 C、 D、10. 关于一次函数 , 下列结论正确的是( )A、图象不经过第二象限 B、图象与x轴的交点是(0,2) C、将一次函数的图象向上平移1个单位长度后,所得图象的函数表达式为 D、点(x1 , y1)和(x2 , y2)在一次函数的图象上,若x1<x2 , 则y1>y2
A、1个 B、2个 C、3个 D、4个9. 已知 , , 是直线为常数)上的三个点,则 , , 的大小关系是A、 B、 C、 D、10. 关于一次函数 , 下列结论正确的是( )A、图象不经过第二象限 B、图象与x轴的交点是(0,2) C、将一次函数的图象向上平移1个单位长度后,所得图象的函数表达式为 D、点(x1 , y1)和(x2 , y2)在一次函数的图象上,若x1<x2 , 则y1>y2二、填空题(每题3分,共18分)
-
11. 如图,直线分别与x、y轴交于点A、B , 点C在线段上,线段沿翻折,点O落在边上的点D处.则直线的解析式为 .
 12. 如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标 .
12. 如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标 . 13. 如图,直线与轴、轴分别交于 , 两点,以为边在轴右侧作等边 , 将点向左平移,使其对应点恰好落在直线上,则点的坐标为 .
13. 如图,直线与轴、轴分别交于 , 两点,以为边在轴右侧作等边 , 将点向左平移,使其对应点恰好落在直线上,则点的坐标为 . 14. 如图所示,在平面直角坐标系中,线段AB所在直线的函数表达式为y=-x+4,C是AO的中点,P是AB上一动点,则PO+PC的最小值是.
14. 如图所示,在平面直角坐标系中,线段AB所在直线的函数表达式为y=-x+4,C是AO的中点,P是AB上一动点,则PO+PC的最小值是. 15. 如图,已知A地在B地正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为千米.
15. 如图,已知A地在B地正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为千米. 16. 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴于点A3 , …,按此做法进行下去,点An的坐标为
16. 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴于点A3 , …,按此做法进行下去,点An的坐标为
三、解答题(共8题,共72分)
-
17. 如图,在平面直角坐标系xOy中,一次函数的图象经过点A(﹣3,0)与点B(0,4).(1)、求这个一次函数的表达式;(2)、点P为x轴上一动点,且△ABP是等腰三角形,请直接写出点P的坐标.18. 【学习材料】
求直线向右平移个单位长度后的解析式.
第一步,在直线上任意取两点和;
第二步,将点和向右平移个单位长度得到点和 , 则直线就是直线向右平移个单位长度后得到的直线;
第三步,设直线的解析式为: , 将和代入得到:解得 , 所以直线的解析式为: .
(1)、【类比思考】若将直线向左平移个单位长度,则平移后的直线解析式为 ;
若先将直线向右平移个单位长度,再向下平移个单位长度,得到直线 , 则直线的解析式为 .
(2)、【拓展应用】已知一次函数的图象与直线关于轴对称,求一次函数的解析式;
若一次函数的图象绕点逆时针旋转后得到直线 , 则直线的解析式为 ▲ .
19. 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.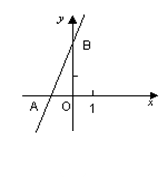 (1)、求△AOB的面积;
(1)、求△AOB的面积;
(2)、过B点作直线BP与x轴相交于P,△ABP的面积是 ,求点P的坐标.
20. 小林同学从家出发,步行到离家a米的公园散步,速度为50米/分钟:6分钟后哥哥也从家出发沿着同一路线骑自行车到公园,哥哥到达公园后立即以原速返回家中,两人离家的距离y(米)与小林出发的时间x(分钟)的函数关系如图所示. (1)、 ;(2)、求所在直线的函数表达式;(3)、小林与哥哥第二次相遇时距离公园还有多远?21. (阅读材料)在平面直角坐标系中,点P(x0 , y0)到直线Ax+By+C=0的距离公式是
(1)、 ;(2)、求所在直线的函数表达式;(3)、小林与哥哥第二次相遇时距离公园还有多远?21. (阅读材料)在平面直角坐标系中,点P(x0 , y0)到直线Ax+By+C=0的距离公式是如:求点P(1,2)到直线y=﹣ x+1的距离d
解:将直线解析式变形为4x+3y﹣3=0,则A=4,B=3,C=﹣3
所以
(解决问题)已知直线l1的解析式是y=- x+1
(1)、若点P的坐标为(1,﹣2),则点P到直线l1的距离是 ;(2)、若直线l2与直线l1平行,且两条平行线间的距离是 ,请求出直线l2的解析式.22. 在平面直角坐标系中,正比例函数的图象经过点 , 过点A的直线与x轴、y轴分别交于B , C两点. (1)、求正比例函数的表达式;(2)、若的面积为的面积的倍,求直线的表达式;(3)、在(2)的条件下,在线段上找一点D , 使平分 , 求点D的坐标.23. 如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,过点B的直线交x轴与点
(1)、求正比例函数的表达式;(2)、若的面积为的面积的倍,求直线的表达式;(3)、在(2)的条件下,在线段上找一点D , 使平分 , 求点D的坐标.23. 如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,过点B的直线交x轴与点 (1)、点A坐标为 , 点B坐标为;(2)、求直线的表达式;(3)、若点D在直线上,且是以为腰的等腰三角形,点D的坐标.24. 如图,A,B是分别在x轴上的原点左右侧的点,点P(2,m)在第一象限内,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOC=10.
(1)、点A坐标为 , 点B坐标为;(2)、求直线的表达式;(3)、若点D在直线上,且是以为腰的等腰三角形,点D的坐标.24. 如图,A,B是分别在x轴上的原点左右侧的点,点P(2,m)在第一象限内,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOC=10. (1)、求点A的坐标及m的值;(2)、若S△BOP=S△DOP , 求直线BD的解析式;(3)、在(2)的条件下,直线AP上是否存在一点Q,使△QAO的面积等于△BOD面积?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求点A的坐标及m的值;(2)、若S△BOP=S△DOP , 求直线BD的解析式;(3)、在(2)的条件下,直线AP上是否存在一点Q,使△QAO的面积等于△BOD面积?若存在,求出点Q的坐标;若不存在,请说明理由.