北师大版数学九年级上册《第四章 图形的相似》单元同步测试卷
试卷更新日期:2024-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 已知 , 若 , 则=( )A、12 B、15 C、16 D、12. 如图,已知AB//CD//EF , AD∶AF=3∶5,BE=10,则BC的长等于( )
 A、4 B、5 C、6 D、73. 下列各组图形中,一定相似的是( )A、两个平行四边形 B、两个正方形 C、两个菱形 D、两个矩形4. 在长度为1的线段上找到两个黄金分割点P,Q,则PQ=( )A、 B、 C、 D、5. 如图,已知在 , 为上一点,连结 , 不能判断的是( )
A、4 B、5 C、6 D、73. 下列各组图形中,一定相似的是( )A、两个平行四边形 B、两个正方形 C、两个菱形 D、两个矩形4. 在长度为1的线段上找到两个黄金分割点P,Q,则PQ=( )A、 B、 C、 D、5. 如图,已知在 , 为上一点,连结 , 不能判断的是( ) A、 B、 C、 D、6. 如图,下列条件不能判定的是( )
A、 B、 C、 D、6. 如图,下列条件不能判定的是( ) A、 , B、 C、 , D、 ,7. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、 , B、 C、 , D、 ,7. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( ) A、
A、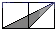 B、
B、 C、
C、 D、
D、 8. 约在两千五百年前,如图(1),墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )
8. 约在两千五百年前,如图(1),墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( ) A、4cm B、4.5cm C、5cm D、5.5cm9. 若与相似且对应中线之比为 , 则周长之比和面积比分别是( )A、 , B、 , C、 , D、 ,10. 如图,在平面直角坐标系中,和是以原点为位似中心的位似图形.若 , 的周长为3,则的周长为( )
A、4cm B、4.5cm C、5cm D、5.5cm9. 若与相似且对应中线之比为 , 则周长之比和面积比分别是( )A、 , B、 , C、 , D、 ,10. 如图,在平面直角坐标系中,和是以原点为位似中心的位似图形.若 , 的周长为3,则的周长为( ) A、6 B、9 C、12 D、30
A、6 B、9 C、12 D、30二、填空题(每题3分,共18分)
-
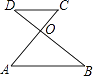
11. 如图,线段AC、BD交于点O,请你添加一个条件: , 使△AOB∽△COD.
 12. 若 , 则 .13. 如图,四边形四边形 , 则的度数是 .
12. 若 , 则 .13. 如图,四边形四边形 , 则的度数是 . 14. 如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退保持脚、镜和旗杆底端在同一直线上 , 直到她刚好在镜子中看到旗杆的顶端已知小艺的眼睛离地面高度为米,同时量得小艺与镜子的水平距离为米,镜子与旗杆的水平距离为米,则旗杆的高度为 米
14. 如图,数学活动课上,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退保持脚、镜和旗杆底端在同一直线上 , 直到她刚好在镜子中看到旗杆的顶端已知小艺的眼睛离地面高度为米,同时量得小艺与镜子的水平距离为米,镜子与旗杆的水平距离为米,则旗杆的高度为 米 15. 若 , 且 , 的面积为 , 则的面积为.16. 如图,的顶点坐标是 , , , 以点O为位似中心,将缩小为原来的 , 得到 , 则点的坐标为.
15. 若 , 且 , 的面积为 , 则的面积为.16. 如图,的顶点坐标是 , , , 以点O为位似中心,将缩小为原来的 , 得到 , 则点的坐标为.
三、解答题(共8题,共72分)
-
17. 如图,在矩形ABCD中,点E是BC的中点,连接AE , 过点D作AE的垂线分别交AE , AB于点F , G .
 (1)、求证:;(2)、若 , , 求AE的长.18. 如图,△ABC∽△ACD .
(1)、求证:;(2)、若 , , 求AE的长.18. 如图,△ABC∽△ACD . (1)、若CD平分∠ACB , ∠ACD=40° , 求∠ADC的度数.(2)、若AD=2,BD=3,求AC的长.19. 如图,已知直线 , , 分别截直线于点 , , , 截直线于点 , , , 且.
(1)、若CD平分∠ACB , ∠ACD=40° , 求∠ADC的度数.(2)、若AD=2,BD=3,求AC的长.19. 如图,已知直线 , , 分别截直线于点 , , , 截直线于点 , , , 且. (1)、如果 , , , 求的长;(2)、如果 , , 求的长.20.
(1)、如果 , , , 求的长;(2)、如果 , , 求的长.20.如图所示的网格中,每个小方格都是边长为1的小正方形,B(﹣1,﹣1),C(5,﹣1)
 (1)、把△ABC绕点C按顺时针旋转90°后得到△A1B1C1 , 请画出这个三角形并写出点B1的坐标;(2)、以点A为位似中心放大△ABC,得到△A2B2C2 , 使放大前后的面积之比为1:4,请在下面网格内出△A2B2C2 .21. 如图, , .
(1)、把△ABC绕点C按顺时针旋转90°后得到△A1B1C1 , 请画出这个三角形并写出点B1的坐标;(2)、以点A为位似中心放大△ABC,得到△A2B2C2 , 使放大前后的面积之比为1:4,请在下面网格内出△A2B2C2 .21. 如图, , .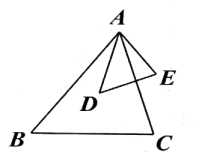 (1)、与相似吗?为什么?(2)、如果 , , 那么的长为多少?22. 如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.
(1)、与相似吗?为什么?(2)、如果 , , 那么的长为多少?22. 如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.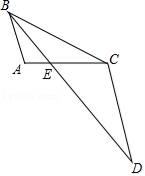 (1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.
(1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.
23. 已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3 cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为 cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题: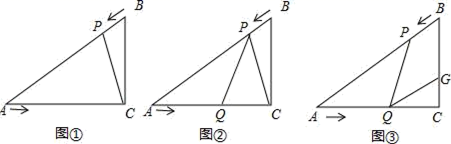 (1)、如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;(2)、如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;(3)、如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.24. 问题提出:已知矩形 , 点为上的一点, , 交于点 . 将绕点顺时针旋转得到 , 则与有怎样的数量关系.
(1)、如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;(2)、如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;(3)、如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.24. 问题提出:已知矩形 , 点为上的一点, , 交于点 . 将绕点顺时针旋转得到 , 则与有怎样的数量关系. (1)、【问题探究】
(1)、【问题探究】探究一:如图,已知正方形 , 点为上的一点, , 交于点 .
如图1,直接写出的值;(2)、将绕点顺时针旋转到如图所示的位置,连接、 , 猜想与的数量关系,并证明你的结论;(3)、探究二:如图,已知矩形 , 点为上的一点, , 交于点 .如图3,若四边形为矩形, , 将绕点顺时针旋转得到、的对应点分别为、点 , 连接、 , 则的值是否随着的变化而变化.若变化,请说明变化情况;若不变,请求出的值.
(4)、【一般规律】
如图3,若四边形为矩形, , 其它条件都不变,将绕点顺时针旋转得到 , 连接 , , 请直接写出与的数量关系.