北师大版数学九年级上册《第四章图形的相似》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 若 $\frac{a}{2} = \frac{b}{3} \neq 0$ ，则 $\frac{a + b}{a - 2 b}$ 的值是（）

A、 $\frac{4}{5}$ B、 $- \frac{4}{5}$ C、 $\frac{5}{4}$ D、 $- \frac{5}{4}$

查看试题解析
2. 如图，在菱形 $A B C D$ 中，对角线交点为O ， E是 $A D$ 的中点，作 $E F ⊥ B D$ 于点F ， $E G ⊥ A C$ 于点G ，连接 $F G$ ．若 $A C = 10 ， B D = 24$ ，则 $F G$ 的长为（）

A、12 B、10 C、 $6.5$ D、5

查看试题解析
3. 下列网格中各个小正方形的边长均为1，阴影部分图形分别记作甲、乙、丙、丁，其中是相似形的为（）

A、甲和乙 B、乙和丁 C、甲和丙 D、甲和丁

查看试题解析
4. 如图，在正方形ABCD中，点E ， F分别为对角线BD ， AC的三等分点，连接AE并延长交CD于点G ，连接EF ， FG ．若∠AGF＝α，则∠FAG用含α的代数式表示为（　　）

A、 $\frac{4 5^{∘} - α}{2}$ B、 $\frac{9 0^{∘} - α}{2}$ C、 $\frac{4 5^{∘} + α}{2}$ D、 $\frac{α}{2}$

查看试题解析
5. 如图， $B E$ 为驾驶员盲区，驾驶员的眼睛点 $P$ 处与地面 $B E$ 的距离为1.6米，车头 $A C D F$ 近似看成一个矩形，且满足 $2 A F = 3 D F$ ，若车 $A F$ 宽的长为1.8米，则盲区 $B E$ 的长是（）

A、5.4米 B、6米 C、7.2米 D、8米

查看试题解析
6. 如图，点D、E分别是AB、AC的中点，则 $S_{△ A D E}$ ：S_四边形_DBCE=（）

A、1：2 B、1：3 C、1：4 D、2：3

查看试题解析
7. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（）

A、（3，2） B、（3，1） C、（2，2） D、（4，2）

查看试题解析
8. 如图，在矩形 $A B C D$ 中， $A F$ 平分 $∠ B A C$ ，将矩形沿直线 $E F$ 折叠，使点A ， B分别落在边 $A D 、 B C$ 上的点 $A^{'}$ ， $B^{'}$ 处， $E F$ ， $A^{'} F$ 分别交 $A C$ 于点G ， H ．若 $G H = 2$ ， $H C = 8$ ，则 $B F$ 的长为（）

A、 $\frac{20 \sqrt{2}}{9}$ B、 $\frac{20 \sqrt{3}}{9}$ C、 $\frac{5 \sqrt{3}}{2}$ D、5

查看试题解析
9. 如图， $△ A B C$ 中， $A B = B C = 1$ ， $∠ C = 72 °$ .将 $△ A B C$ 绕点A顺时针旋转得到 $△ A B^{'} C^{'}$ ，点 $B'$ 与点B是对应点，点 $C^{'}$ 与点C是对应点.若点 $C^{'}$ 恰好落在BC边上，下列结论：①点B在旋转过程中经过的路径长是 $\frac{1}{5} π$ ；② $B^{'} A / / B C$ ；③ $B D = C^{'} D$ ；④ $\frac{A B}{A C} = \frac{B^{'} B}{B D}$ .其中正确的结论是( )

A、①②③④ B、①②③ C、①③④ D、②④

查看试题解析
10. 如图，已知 $A C$ 是矩形 $A B C D$ 的对角线，以点 $D$ 为旋转中心将 $△ A D C$ 逆时针旋转 $90 °$ ，得到 $△ F D E$ ， $B$ ， $F$ ， $E$ 三点恰好在同一条直线上，设 $A C$ 与 $B E$ 相交于点 $G$ ，连结 $D G .$ 有以下结论： $① A C ⊥ B E$ ； $② △ B C G$ ∽ $△ G A D$ ； $③ F$ 是线段 $C D$ 的黄金分割点； $④ C G + \sqrt{2} D G = E G .$ 其中正确的是( )

A、 $①$ B、 $① ③$ C、 $② ④$ D、 $① ③ ④$

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，正方形ABCD的对角线AC ， BD相交于点O ，点E是OA的中点，点F是OD上一点，连接EF ．若∠FEO＝45°，则 $\frac{E F}{B C}$ 的值为．

查看试题解析
12. 如图，在四边形 $A B C D$ 中， $∠ B C D = 90 °$ ，对角线 $A C ， B D$ 相交于点 $O$ ．若 $A B = A C = 5 ， B C = 6 ， ∠ A D B = 2 ∠ C B D$ ，则 $A D$ 的长为．

查看试题解析
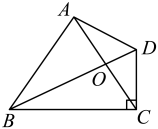13. 如图，这是小孔成像的示意图，光线经过小孔O ，物体AB在幕布上形成倒立的实像CD（点A ， B的对应点分别是C ， D）．若物体AB的高为 $6 c m$ ，实像CD的高度为 $4 c m$ ，则小孔O的高度OE为 $c m$ ．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $A E ⊥ C D$ 于 $E$ ， $A E = A B$ ， $, E F ⊥ A D$ 于 $F$ ，延长 $F E$ 、 $B C$ 交于点 $G$ ，若 $\frac{F E}{E G} = \frac{3}{2}$ ， $A D = \sqrt{34}$ ，则线段 $E F$ 的长为．

查看试题解析
15. 如图，在正方形 $A B C D$ ，点 $E$ ， $F$ 在射线 $B C$ 上， $∠ E A F = 45 °$ ，则 $\frac{B E}{E F}$ 最大值是．

查看试题解析
16. 如图，在Rt△ABC中，∠C=90°，点D是AC边上的一点，DE垂直平分AB，垂足为点E.若AC=8，BC=6，则线段DE的长度为.

查看试题解析

三、解答题（共8题，共72分）

17. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是 $B C$ 的中点，点E在 $B A$ 的延长线上，点F在边 $A C$ 上， $∠ E D F = ∠ B$ ．

(1)、求证： $△ B D E ∽ △ C F D$ ．

(2)、当 $A B = 10$ ， $∠ B = 30 °$ ，求 $C F \cdot B E$ 的值．

查看试题解析
18. 如图，点D是 $△ A B C$ 边 $A C$ 的上一点，且 $∠ A B D = ∠ C$ ，

(1)、求证： $△ A B D ∽ △ A C B$

(2)、如果 $A D = 1, A C = 4$ ，求 $A B$ 的值．

查看试题解析
19. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 4$ ， $E$ 是边 $B C$ 上的一点（不与 $B$ 、 $C$ 重合）， $D F ⊥ A E$ ，垂足为 $F$ ．

(1)、求证： $△ A B E ∽ △ D F A$ ；

(2)、若 $S_{△ D F A} = \frac{1}{3} S_{△ A B E}$ ，求 $B E$ 的长．

查看试题解析
20. 已知如图，在 $△ A B C$ 中，点D是 $A B$ 边上一个动点，连接 $C D$ ，在 $C D$ 的右侧作 $∠ C D E$ ， $D E$ 边交 $B C$ 于点E ，当点D在 $A B$ 边上运动时（点D不与点A、点B重合），始终保持 $∠ A = ∠ C D E$ ．

(1)、你能否再添加一个条件，使 $△ A C D ∽ △ B D E$ ；

(2)、在（1）的条件下，当 $A C = 4$ ， $B E = 3$ ， $A B = 8$ 时，求A、D两点之间的距离．

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中， $E$ 为 $D C$ 边上一点， $∠ E A B = ∠ E B C$ ．

(1)、求证： $△ A B E$ ∽ $△ B E C$ ；

(2)、若 $A B = 4$ ， $D E = 3$ ，求 $B E$ 的长．

查看试题解析
22. 如图，矩形 $A B C D$ 具有下列特征：在边 $A B$ 上取点 $E$ ，连接 $D E$ ， $C E$ ，当 $D E$ 平分 $∠ A D C$ 时，将 $△ B C E$ 沿 $C E$ 翻折，点 $B$ 恰在线段 $D E$ 上．

(1)、这样的矩形，长 $A B$ 与宽 $A D$ 之比为；

(2)、如图 $2$ ，连接 $A F$ 并延长交 $C E$ 于 $G$ ，判断 $△ E F G$ 的形状并证明；

(3)、在图 $2$ 中，有无与 $△ A E G$ 相似的三角形？并证明你的结论．

查看试题解析
23.

(1)、问题背景：如图 $(1)$ ，已知 $△ A B C$ ∽ $△ A D E$ ，求证： $△ A B D$ ∽ $△ A C E$ ；

(2)、尝试应用：如图 $(2)$ ，在 $△ A B C$ 和 $△ A D E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $∠ A B C = ∠ A D E = 30 °$ ， $A C$ 与 $D E$ 相交于点 $F .$ 点 $D$ 在 $B C$ 边上， $\frac{A D}{B D} = \sqrt{3}$ ，求 $\frac{D F}{C F}$ 的值．

查看试题解析
24. 综合与实践
主题：某数学实践小组以标准对数视力表为例，探索视力表中的数学知识
操作：步骤一：用硬纸板复制视力表中视力为0.1，0.2所对应的“E”，并依次编号为①，②，垂直放在水平桌面上，开口的底部与桌面的接触点为 $D_{1}$ ， $D_{2}$ ；
步骤二：如1图所示，将②号“E”沿水平桌面向右移动，直至从观测点O看去，对应顶点 $P_{1}$ ， $P_{2}$ 与点O在一条直线上为止．
结论：这时我们说，在 $D_{1}$ 处用①号“E”测得的视力与在 $D_{2}$ 处用②号“E”测得的视力相同．

(1)、探究：①如1图， $\frac{b_{1}}{l_{1}}$ 与 $\frac{b_{2}}{l_{2}}$ 之间存在什么关系?请说明理由；
②由标准视力表中的 $b_{1} = 72 m m$ ， $l_{1} = 5 m$ ，可计算出 $l_{2} = 3 m$ 时， $b_{2} =$ mm；

(2)、运用：如果将视力表中的两个“E”放在如2图所示的平面直角坐标系中，两个“E”字是位似图形，位似中心为点O ， ①号“E”与②号“E”的相似比为 $2 : 1$ ，点P与点Q为一组对应点．
若点Q的坐标为 $(- 3, 4)$ ，则点P的坐标为．

查看试题解析

北师大版数学九年级上册《第四章 图形的相似》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学九年级上册《第四章图形的相似》单元提升测试卷