浙教版数学九年级上册《第4章 相似三角形》单元同步测试卷
试卷更新日期:2024-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 已知2x=5y(y≠0),则下列比例式成立的是( )A、 B、 C、 D、2. 如图,在△ABC中,O是边AB的中点.按下列要求作图:①以点B为圆心、适当长为半径画弧,交线段BO于点D , 交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G , 点G与点C在直线AB同侧;④作直线OG , 交AC于点M . 下列结论不一定成立的是( )
 A、∠AOM=∠B B、∠OMC+∠C=180° C、AM=CM D、OMAB3. 如图,已知 , 它们依次交直线、于点、、和点、、 , 如果:: , , 那么的长等于( )
A、∠AOM=∠B B、∠OMC+∠C=180° C、AM=CM D、OMAB3. 如图,已知 , 它们依次交直线、于点、、和点、、 , 如果:: , , 那么的长等于( ) A、 B、 C、 D、4. 如图,D是边延长线上一点,添加一个条件后,仍不能使的是( )
A、 B、 C、 D、4. 如图,D是边延长线上一点,添加一个条件后,仍不能使的是( )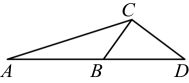 A、 B、 C、 D、5. 如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:① , ② , ③ , ④ , ⑤ , 使与一定相似的有( )
A、 B、 C、 D、5. 如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:① , ② , ③ , ④ , ⑤ , 使与一定相似的有( )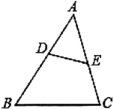 A、①②④ B、②④⑤ C、①②③④ D、①②③⑤6. 下列各组三角形中,根据所给条件不能判断与相似的是( ).A、
A、①②④ B、②④⑤ C、①②③④ D、①②③⑤6. 下列各组三角形中,根据所给条件不能判断与相似的是( ).A、 B、
B、 C、
C、 D、
D、 7. 中国古代经典数学著作《孙子算经》有首歌谣:“今有笔不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸、问华长几何?”其大意是:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆(如图),它的影长五寸(备注:1丈尺,1尺=10寸),问竹竿长多少?若设竹竿长尺,则可列方程为( )
7. 中国古代经典数学著作《孙子算经》有首歌谣:“今有笔不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸、问华长几何?”其大意是:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆(如图),它的影长五寸(备注:1丈尺,1尺=10寸),问竹竿长多少?若设竹竿长尺,则可列方程为( ) A、 B、 C、 D、8. 如图,在 中, ,则 的值是( )
A、 B、 C、 D、8. 如图,在 中, ,则 的值是( )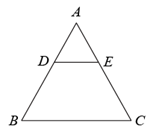 A、 B、 C、 D、9. 如图,在中, , , 下列结论一定正确的是( )
A、 B、 C、 D、9. 如图,在中, , , 下列结论一定正确的是( )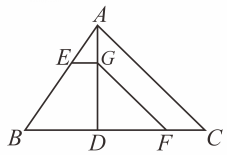 A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )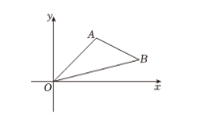 A、(1,1) B、(4,4)或(8,2) C、(4,4) D、(4,4)或(-4,-4)
A、(1,1) B、(4,4)或(8,2) C、(4,4) D、(4,4)或(-4,-4)二、填空题(每题3分,共18分)
-
11. 如图, , 请你添加一个条件: , 使 , (只需写出一个满足题目要求的条件即可).
 12. 如图, , ,则图中相似三角形有对.
12. 如图, , ,则图中相似三角形有对. 13. 如图,在平行四边形中,是线段上一点,连结、交于点.若 , 则.
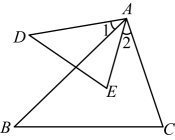
13. 如图,在平行四边形中,是线段上一点,连结、交于点.若 , 则. 14. 如图所示,已知在中,是边AB上的一点,的平分线AQ分别与CD,BC交于点P,Q,那么的值为.
14. 如图所示,已知在中,是边AB上的一点,的平分线AQ分别与CD,BC交于点P,Q,那么的值为. 15. 如图,四边形ABCD∽四边形A'B'C'D',若∠B=60°,∠C=80°,∠A'=100°,则∠D= .
15. 如图,四边形ABCD∽四边形A'B'C'D',若∠B=60°,∠C=80°,∠A'=100°,则∠D= . 16. 如图所示,在直角坐标系中,与是位似图形,则位似中心的坐标为.
16. 如图所示,在直角坐标系中,与是位似图形,则位似中心的坐标为.
三、解答题(共9题,共72分)
-
17. 已知 , 求值:(1)、(2)、18. 如图,正方形ABCD中,AB=9,E是BC上一点,过E作EF⊥AE交CD于点F,连接AF.
 (1)、证明:ΔABE∽ΔECF.(2)、当BE=3时,求CF的长.19. 如图,在 中, 为 上一点, .
(1)、证明:ΔABE∽ΔECF.(2)、当BE=3时,求CF的长.19. 如图,在 中, 为 上一点, .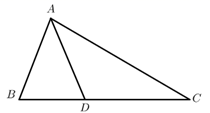 (1)、求证: .(2)、若 ,求 的长.20. 如图,在 中, , , ,且 .
(1)、求证: .(2)、若 ,求 的长.20. 如图,在 中, , , ,且 . (1)、求 的长;(2)、求证: .21. 如图,点E在矩形ABCD的边AD上,且∠EBC=∠ECB.
(1)、求 的长;(2)、求证: .21. 如图,点E在矩形ABCD的边AD上,且∠EBC=∠ECB. (1)、求证:AE=ED;(2)、连接BD交CB于点F,求△BCF和△DEF的面积之比.22. 如图,AE为△ABC外接圆⊙O的直径,AD为△ABC的高.
(1)、求证:AE=ED;(2)、连接BD交CB于点F,求△BCF和△DEF的面积之比.22. 如图,AE为△ABC外接圆⊙O的直径,AD为△ABC的高.
求证:(1)、∠BAD=∠EAC;
(2)、AB•AC=AD•AE
23. 矩形ABCD中,E为BC上一点,DF⊥AE于点F. (1)、求证:△ABE∽△DFA;(2)、若AB=6,AD=12,AE=10,求DF的长.
(1)、求证:△ABE∽△DFA;(2)、若AB=6,AD=12,AE=10,求DF的长.

