浙教版数学九年级上册《第4章 相似三角形》单元提升测试卷
试卷更新日期:2024-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在▱ABCD中,对角线AC , BD交于点O , 点E在BC上,点F在CD上,连接AE , AF , EF , EF交AC于点G . 下列结论错误的是( )
 A、若 , 则EF∥BD B、若AE⊥BC , AF⊥CD , AE=AF , 则EF∥BD C、若EF∥BD , CE=CF , 则∠EAC=∠FAC D、若AB=AD , AE=AF , 则EF∥BD2. 如图,在▱中, , , 的平分线分别交于点 , , 与交于点若 , , , 则( )
A、若 , 则EF∥BD B、若AE⊥BC , AF⊥CD , AE=AF , 则EF∥BD C、若EF∥BD , CE=CF , 则∠EAC=∠FAC D、若AB=AD , AE=AF , 则EF∥BD2. 如图,在▱中, , , 的平分线分别交于点 , , 与交于点若 , , , 则( ) A、 B、 C、 D、3. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A、 B、 C、 D、3. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,已知钝角 , 以顶点为圆心,适当长为半径画弧,分别交、于点、 , 再分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , 作射线 , 过点作 , 垂足为点 , 过点作 , 交于点 . 若 , 则的长为( )
4. 如图,已知钝角 , 以顶点为圆心,适当长为半径画弧,分别交、于点、 , 再分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , 作射线 , 过点作 , 垂足为点 , 过点作 , 交于点 . 若 , 则的长为( ) A、 B、 C、 D、55. 如图,点F是平行四边形ABCD的边CD上一点,直线BF交AD的延长线与点E , 则下列结论错误的是( )
A、 B、 C、 D、55. 如图,点F是平行四边形ABCD的边CD上一点,直线BF交AD的延长线与点E , 则下列结论错误的是( ) A、 B、 C、 D、6. 如图, 边长为 5 的正方形 分别为各边中点. 连接 , 交点分别为 , 那么四边形 的面积为( )
A、 B、 C、 D、6. 如图, 边长为 5 的正方形 分别为各边中点. 连接 , 交点分别为 , 那么四边形 的面积为( ) A、1 B、2 C、5 D、107. 如图所示为一张矩形纸片ABCD,E为AD的中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C.若的值为( )
A、1 B、2 C、5 D、107. 如图所示为一张矩形纸片ABCD,E为AD的中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C.若的值为( ) A、2 B、 C、 D、8. 如图,正方形中,平分 , 交于点E , 将绕点B顺时针旋转得到 , 延长交于点G , 连接交于点H .
A、2 B、 C、 D、8. 如图,正方形中,平分 , 交于点E , 将绕点B顺时针旋转得到 , 延长交于点G , 连接交于点H .下列结论①;②;③;④
正确的是( )
 A、①②③④ B、②③ C、①③ D、①②④9. 如图,已知平行四边形 , 点E是延长线上一点,与分别相交于点 . 则下列关系式成立的是( )
A、①②③④ B、②③ C、①③ D、①②④9. 如图,已知平行四边形 , 点E是延长线上一点,与分别相交于点 . 则下列关系式成立的是( ) A、 B、 C、 D、10. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )
A、 B、 C、 D、10. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )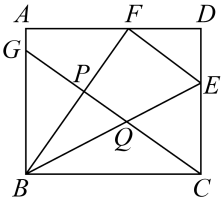 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在梯形ABCD中, , 对角线AC和BD交于点O , 若 , 则 .
 12. 已知===k,则k的值是 .
12. 已知===k,则k的值是 .
13. 如图所示,要使得 , 需要补充一个条件可以是。(只需要填写一个即可) 14. 如图, 在边长为6的等边△ABC中, D是BC边上动点, ∠EDF=60°, E、F分别在AB、AC边上. 若BD=2, FC=3,则BE=.
14. 如图, 在边长为6的等边△ABC中, D是BC边上动点, ∠EDF=60°, E、F分别在AB、AC边上. 若BD=2, FC=3,则BE=. 15. 如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且 . 若A(9,3),则A1点的坐标是 .
15. 如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且 . 若A(9,3),则A1点的坐标是 . 16. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .
16. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .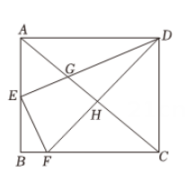
三、解答题(共8题,共72分
-
17. 如图,在锐角三角形ABC中,AC>BC.以点C为圆心,BC长为半径画弧,交边AB于点D,连结CD.点E是CB延长线上的一点,连结AE,若AB平分∠CAE.
 (1)、求证:.(2)、当 , 求的值.18. 如图,D , E为△GCF中GF边上两点,过D作AB∥CF交CE的延长线于点A , AE=CE .
(1)、求证:.(2)、当 , 求的值.18. 如图,D , E为△GCF中GF边上两点,过D作AB∥CF交CE的延长线于点A , AE=CE . (1)、求证:△ADE≌△CFE;(2)、若BD=1,GB=2,BC=3,求AB的长.19. 如图,在四边形ABCD中,∠A=90°,连接BD , 过点C作CE⊥AB , 垂足为E , CE交BD于点F , ∠1=∠ABC .
(1)、求证:△ADE≌△CFE;(2)、若BD=1,GB=2,BC=3,求AB的长.19. 如图,在四边形ABCD中,∠A=90°,连接BD , 过点C作CE⊥AB , 垂足为E , CE交BD于点F , ∠1=∠ABC . (1)、求证:∠2=∠3;(2)、若∠4=45°.
(1)、求证:∠2=∠3;(2)、若∠4=45°.①请判断线段BC , BD的数量关系,并证明你的结论;
②若BC=13,AD=5,求EF的长.
20. 正方形边长为3,点E是上一点,连结交于点F . (1)、如图1,若 , 求的值;(2)、如图1, , 若 , 求m的值.(3)、如图2,点G为上一点,且满足 , 设 , 试探究y与x的函数关系.21. 垂中平行四边形的定义如下: 在平行四边形中,过一个顶点作关于不相邻的两个顶点的对角线的垂线交平行四边形的一条边, 若交点是这条边的中点, 则该平行四边形是 “垂中平行四边形”.(1)、 如图所示, 四边形 为 “垂中平行四边形”, , 则 ;;
(1)、如图1,若 , 求的值;(2)、如图1, , 若 , 求m的值.(3)、如图2,点G为上一点,且满足 , 设 , 试探究y与x的函数关系.21. 垂中平行四边形的定义如下: 在平行四边形中,过一个顶点作关于不相邻的两个顶点的对角线的垂线交平行四边形的一条边, 若交点是这条边的中点, 则该平行四边形是 “垂中平行四边形”.(1)、 如图所示, 四边形 为 “垂中平行四边形”, , 则 ;; (2)、 如图 2, 若四边形 为 “垂中平行四边形”, 且 , 猜想 与 的关系,并说明理由;
(2)、 如图 2, 若四边形 为 “垂中平行四边形”, 且 , 猜想 与 的关系,并说明理由; (3)、①如图 3 所示, 在 中, 交 于点 , 请画出以 为边的垂中平行四边形, 要求: 点 在垂中平行四边形的一条边上 (温馨提示: 不限作图工具);
(3)、①如图 3 所示, 在 中, 交 于点 , 请画出以 为边的垂中平行四边形, 要求: 点 在垂中平行四边形的一条边上 (温馨提示: 不限作图工具);②若 关于直线 对称得到 , 连接 , 作射线 交①中所画平行四边形的边于点 , 连接 , 请直接写出 的值.
 22. 为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
22. 为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法. (1)、如图1,小张在测量时发现,自己在操场上的影长恰好等于自己的身高 . 此时,小组同学测得旗杆的影长为 , 据此可得旗杆高度为m;(2)、如图2,小李站在操场上E点处,前面水平放置镜面C , 并通过镜面观测到旗杆顶部A . 小组同学测得小李的眼睛距地面高度 , 小李到镜面距离 , 镜面到旗杆的距离 . 求旗杆高度;(3)、小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
(1)、如图1,小张在测量时发现,自己在操场上的影长恰好等于自己的身高 . 此时,小组同学测得旗杆的影长为 , 据此可得旗杆高度为m;(2)、如图2,小李站在操场上E点处,前面水平放置镜面C , 并通过镜面观测到旗杆顶部A . 小组同学测得小李的眼睛距地面高度 , 小李到镜面距离 , 镜面到旗杆的距离 . 求旗杆高度;(3)、小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M , N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q , 标高线始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D , G两点,并标记观测视线与标高线交点C , 测得标高 , . 将观测点D后移到处,采用同样方法,测得 , . 求雕塑高度(结果精确到).

