浙教版数学八年级上册《第4章图形与坐标》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

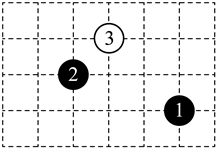
1. 如图，在围棋棋盘上有3枚棋子，如果黑棋①的位置用有序数对 $(0 ， - 1)$ 表示，黑棋②的位置用有序数对 $(- 3 ， 0)$ 表示，则白棋③的位置可用有序数对表示为（）

A、 $(2 ， 1)$ B、 $(- 1 ， 2)$ C、 $(- 2 ， 1)$ D、 $(1 ， - 2)$

查看试题解析
2. 若点 $N (1 - 2 a, a)$ 在第二象限，那么a的取值范围是（）

A、 $a > \frac{1}{2}$ B、 $a < \frac{1}{2}$ C、 $0 < a < \frac{1}{2}$ D、 $0 \leq a < \frac{1}{2}$

查看试题解析
3. 在平面直角坐标系中，点 $P (| a | + 1, - 2)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 在平面直角坐标系中，将点A（﹣2，﹣2）先向右平移6个单位长度再向上平移5个单位长度得到点A'，则点A'的坐标是（）

A、（4，5） B、（4，3） C、（6，3） D、（﹣8，﹣7）

查看试题解析
5. 若点 $P (x - 4 ， 2 x + 6)$ 在平面直角坐标系的第二象限内，则x的取值范围在数轴上可表示为（）

A、 B、 C、 D、

查看试题解析
6. 点 $P (m + 1, 2 m - 7)$ 在第二、四象限角平分线上，则点 $P$ 的坐标为（）

A、 $(2, - 2)$ B、 $(- 2, - 2)$ C、 $(3, - 3)$ D、 $(- 3, - 3)$

查看试题解析
7. 在平面直角坐标系中，将点 $P (1, - 1)$ 向右平移 $2$ 个单位后，得到的点 $P_{1}$ 关于 $x$ 轴的对称点坐标是（）

A、 $(1,1)$ B、 $(3,1)$ C、 $(3, - 1)$ D、 $(1, - 1)$

查看试题解析
8. 已知点A的坐标为 $(1, 2)$ ，直线 $A B ∥ x$ 轴，且 $A B = 6$ ，则点B的坐标为（）

A、 $(5, 2)$ 或 $(4, 2)$ B、 $(6, 2)$ 或 $(- 4, 2)$ C、 $(7, 2)$ 或 $(- 5, 2)$ D、 $(1, 7)$ 或 $(1, - 3)$

查看试题解析
9. 如图，点A的坐标为（1，3），点B在x轴上，把 $△ A O B$ 沿x轴向右平移到 $△ C E D$ ，若四边形ABDC的面积为9，则点C的坐标为（）

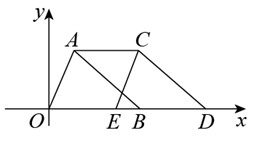A、（1，4） B、（3，4） C、（3，3） D、（4，3）

查看试题解析
10. 平面直角坐标系中，我们把横、纵坐标都是整数，且横、纵坐标之和大于0的点称为“和点”．将某“和点”平移，每次平移的方向取决于该点横、纵坐标之和除以3所得的余数（当余数为0时，向右平移；当余数为1时，向上平移；当余数为2时，向左平移），每次平移1个单位长度．
例：“和点”P（2，1）按上述规则连续平移3次后，到达点P₃（2，2），其平移过程如下： $\begin{array}{l} P (2, 1) \\ 余 0 \end{array} \overset{右}{\to} \begin{array}{l} P_{1} (3, 1) \\ 余 1 \end{array} \overset{上}{\to} \begin{array}{l} P_{2} (3, 2) \\ 余 2 \end{array} \overset{右}{\to} P_{3} (2, 2)$ ．
若“和点”Q按上述规则连续平移16次后，到达点Q₁₆（﹣1，9），则点Q的坐标为（）

A、（6，1）或（7，1） B、（15，﹣7）或（8，0） C、（6，0）或（8，0） D、（5，1）或（7，1）

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，在△ABC中，点A的坐标为（0，1），点B的坐标为（4，1），点C的坐标为（3，4），点D在第一象限（不与点C重合），且△ABD与△ABC全等，点D的坐标是．

查看试题解析
12. 若点 $P (a, b)$ 在第二象限，则 $Q (- b, a)$ 在第象限.

查看试题解析
13. 已知直线 $l_{1}$ ： $y = 2 x + 1$ ，把直线 $l_{1}$ 沿y轴向上平移，得直线 $l_{2}$ ： $y = m x + m - n$ ，则n的取值范围是．

查看试题解析
14. 如图，在 $△ ABC$ 中，点A的坐标为 $(0 ， 1)$ ，点B的坐标为 $(0 ， 4)$ ，点C的坐标为 $(4 ， 3)$ ，点D在第二象限，且 $△ ABD$ 与 $△ ABC$ 全等，点D的坐标是.

查看试题解析
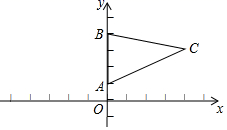15. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB=∠B=30°，OA=2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是

查看试题解析
16. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是．

查看试题解析

三、解答题（共8题，共72分）

17. 已知平面直角坐标系中有一点 $M (m - 1 ， 2 m + 3)$ .

(1)、点M在x轴上，求M的坐标；

(2)、当点 $N (5 ， - 1)$ 且 $M N / / x$ 轴时，求M的坐标.

查看试题解析
18. 已知点A（2-a，a+1）．

(1)、当点A在y轴上时，求a的值．

(2)、当点A在第四象限时，求a的取值范围．

(3)、当点A到x轴的距离是3时，求a的值．

查看试题解析
19.
在平面直角坐标系中，点 $P$ 的坐标为 $(2 m + 1 ， 3 m + 2)$ ．

(1)、若点 $P$ 在过点 $A (- 3 ， 1)$ 且与 $y$ 轴平行的直线上时，求点 $P$ 的坐标；

(2)、将点 $P$ 向右平移 $2$ 个单位，再向上平移 $3$ 个单位后得到点 $M$ ，若点 $M$ 在第三象限，且点 $M$ 到 $y$ 轴的距离为 $7$ ，求点 $M$ 的坐标．

查看试题解析
20. 规定，在平面直角坐标系中，将一个图形先关于y轴对称，再向下平移2个单位记为1次“R变换”．

(1)、画出△ABC经过1次“R变换”后的图形△A₁B₁C₁；

(2)、点A₁坐标为，点B₁坐标为，点C₁坐标为；

(3)、若△ABC边上有一点P（a ， b），经过3次“R变换”后为P₃ ，则P₃的坐标为．

查看试题解析
21. 已知点 $P (2 a - 3 ， a + 6)$ ，解答下列各题．

(1)、点 $P$ 在 $x$ 轴上，求出点 $P$ 的坐标；

(2)、点Q的坐标为 $(3 ， 3)$ ，直线 $P Q // y$ 轴，求出点 $P$ 的坐标：

(3)、若点 $P$ 在第二象限，且它到 $x$ 轴、 $y$ 轴的距离相等，求 $a^{2023} + 2024$ 的值．

查看试题解析
22. 我们学习了平移、旋转、轴对称等图形变换，这些图形变换不仅可以应用到精美的图案设计上，还可以解决生活实际问题.

(1)、【图案设计】
如图1，在平面直角坐标系中， $A (3 ， 4)$ ， $B (1 ， 2)$ ， $C (5 ， 1)$ .
作出 $△ A B C$ 关于 $y$ 轴的对称图形 $△ D E F$ ，并标注出点 $D$ ， $E$ ， $F$ ；

(2)、【拓展应用】
如图1，点 $P$ 是 $x$ 轴上一动点，并且满足 $P A + P B$ 的值最小，请在图中找出点 $P$ 的位置（保留作图痕迹），并直接写出 $P A + P B$ 的最小值为.

(3)、【实际应用】
如图2，某地有一块三角形空地 $A B C$ ，已知 $∠ A B C = 4 5^{∘}$ ， $G$ 是 $△ A B C$ 内一点，连接 $G B$ 后测得 $G B = 20$ 米，现当地政府欲在三角形空地 $A B C$ 中修一个三角形花坛 $G M N$ ，点 $M$ ， $N$ 分别是 $A B$ ， $B C$ 边上的任意一点（不与各边顶点重合），请问 $△ G M N$ 的周长最少约多少米?（保留整数）（ $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
23. 综合与实践：

(1)、问题背景：
已知 $A (1 ， 2)$ ， $B (3 ， 0)$ ， $C (1 ， - 1)$ ， $D (- 3 ， - 3)$ ．在平面直角坐标系中描出这几个点，并分别找到线段 $A B$ 和 $C D$ 中点 $P_{1}$ 、 $P_{2}$ ，然后写出它们的坐标，则 $P_{1}$ ▲ ， $P_{2}$ ▲ ．

(2)、探究发现：
结合上述计算结果，你能发现若线段的两个端点的坐标分别为 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，则线段的中点坐标为．

(3)、拓展应用：
利用上述规律解决下列问题：已知三点 $E (- 1 ， 2)$ ， $F (3 ， 1)$ ， $G (1 ， 4)$ ，第四个点 $H (x ， y)$ 与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．

查看试题解析
24. 如图1，点 $M$ 到点 $O$ 的距离为5个单位，OM与Ox的夹角为 $7 0^{°}$ （Ox的逆时针方向），则点M的位置表示为 $(5 ， 7 0^{°})$ ；同理，点 $N$ 到点 $O$ 的距离为3个单位，ON与Ox的夹角为 $5 0^{°} (O x$ 的顺时针方向），则点 $N$ 的位置表示为 $(3 ， - 5 0^{°})$ .
如图2，已知过点 $O$ 的所有射线等分圆周且相邻两射线的夹角为 $1 5^{°}$ .

(1)、点 $A$ 的位置可表示为；点 $D$ 的位置可表示为.

(2)、请在图2中标出点 $B (5 ， 4 5^{°})$ ，点 $E (2 ， - 9 0^{°})$ .

(3)、怎样从点 $B$ 运动到点 $C$ ？
小明设计的一条路线为：点 $B \to (4 ， 4 5^{°}) \to$ $(3 ， 4 5^{°}) \to (3 ， 3 0^{°}) \to$ 点 $C$ .
请你设计一条与小明不同的路线，也可以从点 $B$ 运动到点 $C$ .

查看试题解析

浙教版数学八年级上册《 第4章 图形与坐标》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

浙教版数学八年级上册《第4章图形与坐标》单元提升测试卷