北师大版数学七年级上册《第三章整式及其加减》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列说法正确的是（）

A、 $- x^{2} y - 2^{2} x^{3} y$ 是六次多项式 B、 $\frac{3 x + y}{3}$ 是单项式 C、 $- \frac{1}{2} π a b$ 的系数是 $- \frac{1}{2} π$ ，次数是2次 D、 $\frac{1}{a}$ +1是多项式

查看试题解析
2. 若多项式 $3 x^{| m |} + (m + 2) x - 7$ 是关于x的二次三项式，则m的值是（）

A、2 B、 $- 2$ C、2或 $- 2$ D、以上答案均不对

查看试题解析
3. 用代数式表示图中阴影部分面积正确的是（）

A、 $a b - \frac{π}{4} a^{2} - \frac{π}{4} b^{2}$ B、 $a b - \frac{π}{2} a^{2}$ C、 $a b - \frac{π}{2} b^{2}$ D、 $\frac{π}{4} a^{2} + \frac{π}{4} b^{2}$

查看试题解析
4. 在式子： $- \frac{3}{8} a b$ ， $\frac{2 x^{2} y}{5}$ ， $\frac{x + y}{2}$ ， $- 2 a^{2} b$ ， 9， $x^{2} - 2 x + 3$ ， $x^{3}$ 中，单项式的个数为（）

A、7个 B、4个 C、6个 D、5个

查看试题解析
5. 把四张形状、大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形的盒子底部，按图甲和图乙两种方式摆放，若长方体盒子底部的长与宽的差为2，则图甲和图乙中阴影部分周长之差为（）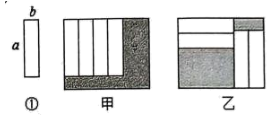

A、4 B、3 C、2 D、1

查看试题解析
6. 一个长方形的周长为 $14 m + 6 n$ ，其中一边的长为 $3 m + 2 n$ ，则另一边的长为 $($ 　　 $)$

A、 $4 m + n$ B、 $7 m + 3 n$ C、 $11 m + 4 n$ D、 $8 m + 2 n$

查看试题解析
7. 把算式： $(- 5) - (- 4) + (- 7) - (- 2)$ 写成省略括号的形式，正确的是（）

A、 $- 5 - 4 + 7 - 2$ B、 $5 + 4 - 7 - 2$ C、 $- 5 + 4 - 7 + 2$ D、 $- 5 + 4 + 7 - 2$

查看试题解析
8. 如图是1个纸杯和6个叠放在一起的纸杯的示意图，量得1个纸杯的高度为8cm，6个叠放在一起的纸杯的高度为12cm，则n个这样的纸杯按照同样方式叠放在一起，总高度(单位：cm)是（）

A、 $8 + \frac{4}{5} n$ B、 $7.2 + \frac{4}{5} n$ C、 $8 + \frac{2}{3} n$ D、 $7.2 + \frac{2}{3} n$

查看试题解析
9. 如图是由一些同样大小的三角形按照一定规律所组成的图形，第1个图有4个三角形．第2个图有7个三角形，第3个图有10个三角形…按照此规律排列下去，第674个图中三角形的个数是（）

A、2022 B、2023 C、2024 D、2025

查看试题解析
10. 已知 $a_{1} = 3 ， a_{2} = \frac{1}{1 - a_{1}} ， a_{3} = \frac{1}{1 - a_{2}} ， a_{4} = \frac{1}{1 - a_{3}} ， \cdot \cdot \cdot$ ，依此类推，则 $a_{2024}$ 等于（）．

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析

二、填空题（每题3分，共18分）

11. 如图所示，是用图形“○”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去，第个“小屋子”中图形“○”个数是图形“●”个数的3倍.

查看试题解析
12. 若一个多项式加上 $y^{2} + 3 x y - 4$ ，结果是 $3 x y + 2 y^{2} - 5$ ，则这个多项式为.

查看试题解析
13. 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示．即：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，……，请你推算2²⁰²⁴的个位数字是．

查看试题解析
14. 小明在化简： $(4 x^{2} - 6 x + 7) - (4 x^{2} - □ x + 2)$ 时发现系数“□”印刷不清楚，老师提示他：“此题的化简结果是常数”，则多项式中的“□”表示的数是.

查看试题解析
15. 如图1，两个正方形分别由①，②两种规格小长方形纸片拼成，现将它们放入一个长为a，宽为b的大长方形中，如图2，其中阴影部分恰好为正方形，则大长方形中未被纸片覆盖部分甲的周长为 .（用含a，b的代数式表示）

查看试题解析
16. 下列说法：
①若 $x^{2} = 1$ ，则 $x = \pm 1$ ；
②单项式 $- 2^{2} a b^{2}$ 和多项式 $x^{3} + x^{2}$ 都是五次整式；
③若 $a + b + c > 0$ ， $a b c < 0$ ，则 $\frac{| a |}{| a |} - \frac{b}{| b |} + \frac{| c |}{c} - \frac{| a b c |}{a b c}$ 的结果有两个；
④若 $2 (a x^{2} - x + 2) - (4 x^{2} + 5 x + a)$ 的运算结果中不含 $x^{2}$ 项，则常数项为 $2$ ．其中一定正确的结论是(只填序号)．

查看试题解析

三、解答题（共8题，共72分）

17. 计算： $3 a^{2} + a^{2} - (2 a^{2} - 2 a) + (3 a - a^{2})$ ．

查看试题解析
18. 计算： $2 a + b + 3 (2 a + 3 b) - 2 (4 a - 6 b)$

查看试题解析
19. 小明准备完成化简： $(□ x^{2} + 6 x + 8) - (6 x + 5 x^{2} + 2)$ ，发现系数“□”印刷不清楚．

(1)、她把“□”猜成4，请你化简 $(4 x^{2} + 6 x + 8) - (6 x + 5 x^{2} + 2)$ ；

(2)、他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”请通过计算说明原题中“□”是什么数．

查看试题解析
20. A、B、C．D四个车站的位置如图所示，车站B距车站A、D的距离分别为 $(a + b) k m$ 、 $(5 a + 36) k m$ ，车站C与车站D的距离为 $(3 a + 2 b) k m$ ．其中a，b是不为0的实数．

(1)、求B、C两站之间的距离（用含a、b的代数式表示）．

(2)、若B、D两个车站之间的距离比A、B两个车站之间的距离长8km，求出B、C两个车站相距多少km？

查看试题解析
21. 如图1，有一块长方形纸板，长是宽的2倍，现将其四角各剪去一个正方形，折成如图2所示的高为 $b c m$ 的无盖长方体盒子（纸板厚度忽略不计）．

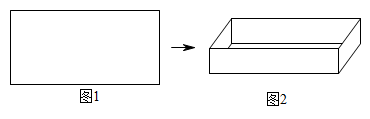(1)、请在图1中的长方形纸板中画出无盖长方体盒子的示意图，用实线表示剪切线，虚线表示折痕．

(2)、如果无盖长方体盒子底面宽为 $a c m$ ，长是宽的3倍，原长方形纸板的长可以用两个不同的代数式表示，则这两个代数式分别为 $c m$ 或 $c m$ ．

(3)、如果原长方形纸板宽为 $x c m$ ，经过剪切折成的无盖长方体盒子底面的周长为（结果化成最简） $c m$ ．

查看试题解析
22. 某超市在双十一期间对顾客实行优惠，规定如下：
一次性购物优惠办法
少于200元不予优惠
低于500元但不低于200元八折优惠
500元或超过500元其中500元部分给予八折优惠，超过500元部分给予七折优惠

(1)、若王老师一次性购物600元，他实际付款元．若王老师实际付款160元，那么王老师一次性购物可能是元；

(2)、若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款元，当x大于或等于500元时，他实际付款元（用含x的代数式表示并化简）；

(3)、如果王老师有两天去超市购物原价合计900元，第一天购物的原价为a元（ $200 < a < 300$ ），用含a的代数式表示这两天购物王老师实际一共付款多少元？当 $a = 250$ 元时，王老师两天一共优惠了多少元？

查看试题解析
23. 已知式子 $M = (a + 4) x^{3} + 6 x^{2} - 2 x + 5$ 是关于 $x$ 的二次多项式，且二次项系数为 $b$ ，数轴上 $A$ ， $B$ 两点所对应的数分别是 $a$ 和 $b$ ．

(1)、则 $a =$ ， $b =$ ； $A$ ， $B$ 两点之间的距离为；

(2)、有一动点 $P$ 从点 $A$ 出发第一次向左运动1个单位长度，然后在新的位置第二次向右运动2个单位长度，再在此位置第三次向左运动3个单位长度…，按照如此规律不断地左右运动，当运动到第2023次时，求点 $P$ 所对应的有理数；

(3)、若点 $A$ 以每秒3个单位长度的速度向左运动，同时点 $B$ 以每秒5个单位长度的速度向右运动，动点 $D$ 从原点开始以每秒 $m (m > 0)$ 个单位长度在 $A ， B$ 之间运动（到达 $A$ 或 $B$ 即停止运动），运动时间为 $t$ 秒，在运动过程中， $B D - 2 A D$ 的值始终保持不变，求 $D$ 点运动的方向及 $m$ 的值．

查看试题解析
24. 【阅读理解】
在计算机上可以设置程序，将二次多项式处理成一次多项式，设置程序为：将二次多项式A的二次项系数乘以2作为一次多项式B的一次项系数，将二次多项式A的一次项系数作为一次多项式B的常数项．
例如： $A = 5 x^{2} - 7 x + 2$ ， A经过程序设置得到 $B = 2 \times 5 x - 7 = 10 x - 7$ ．
【知识应用】
关于x的二次多项式A经过程序设置得到一次多项式B ，已知 $A = x^{2} - x - m$ ，根据上方阅读材料，解决下列问题：

(1)、若 $B = 3 n x - m$ ，求m ， n的值；

(2)、若 $A - m B$ 的结果中不含一次项，求关于x的方程 $B = m$ 的解；

(3)、某同学在计算 $A - 2 B$ 时，把A-2B看成了 $2 A - B$ ，得到的结果是 $2 x^{2} - 4 x - 3$ ，求出 $A - 2 B$ 的正确值．

查看试题解析

一次性购物	优惠办法
少于200元	不予优惠
低于500元但不低于200元	八折优惠
500元或超过500元	其中500元部分给予八折优惠，超过500元部分给予七折优惠

北师大版数学七年级上册《 第三章 整式及其加减》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学七年级上册《第三章整式及其加减》单元提升测试卷