湘教版数学八年级上册《第3章实数》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 矩形相邻两边长分别为 $\sqrt{2}$ cm、 $\sqrt{5}$ cm，设其面积为S cm² ，则S在哪两个连续整数之间（　　）

A、1和2 B、2和3 C、3和4 D、4和5

查看试题解析
2. 如图，数轴上表示实数 $\sqrt{7}$ 的点可能是（）

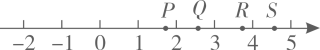A、点P B、点Q C、点R D、点S

查看试题解析
3. 已知a是有理数，b是无理数，下列算式的结果必定为无理数的是（　　）

A、a+b B、ab C、 $\frac{a}{b}$ D、 $\sqrt{a^{2} + b^{2}}$

查看试题解析
4. 在 $- 3$ ， $- 1$ ， π， $\sqrt{5}$ 这四个数中，最小的数是（）

A、 $- 3$ B、 $- 1$ C、π D、 $\sqrt{5}$

查看试题解析
5. 下列说法：①无限小数都是无理数；②无理数都是带根号的数；③负数没有立方根；④ $\sqrt{64}$ 的平方根是±8；⑤无理数减去任意一个有理数仍为无理数．其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 正整数a、b分别满足 $\sqrt[3]{53} < a < \sqrt[3]{98}$ ， $\sqrt{2} < b < \sqrt{7}$ ，则 $b^{a} =$ （）

A、4 B、8 C、9 D、16

查看试题解析
7. 下列语句正确的是（）

A、4是16的算术平方根，即± $\sqrt{16}$ ＝4 B、-3是27的立方根 C、 $\sqrt{64}$ 的立方根是2 D、1的立方根是-1

查看试题解析
8. 如题图数轴上点P表示的数可能是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{10}$

查看试题解析
9. 若6－ $\sqrt{13}$ 的整数部分为x，小数部分为y，则(2x＋ $\sqrt{13}$ )y的值是（）

A、5－3 $\sqrt{13}$ B、3 C、3 $\sqrt{13}$ －5 D、－3

查看试题解析
10. 如果 $\sqrt[3]{23.7} = 2.872$ ， $\sqrt[3]{23700} = 28.72$ ，则 $\sqrt[3]{0.0237} =$ （）

A、0.2872 B、28.72 C、2.872 D、0.02872

查看试题解析

二、填空题（每题3分，共18分）

11. $\sqrt{81}$ 的平方根是．

查看试题解析
12. 若 $2 a - 1$ 的平方根是±3，则 $a =$ ．

查看试题解析
13. 对于实数x，用 $[x]$ 表示不超过x的最大整数，记 ${x} = x - [x]$ ．如 $[3.14] = 3$ ， ${3.14} = 0.14$ ，若 $a = [3 - \sqrt{2}]$ ， $b = {3 - \sqrt{2}}$ ，则代数式 $(a + \sqrt{2}) b =$ ．（要求答案为具体的数值）

查看试题解析
14. 若 $\sqrt{19}$ +1的值在两个整数a与a+1之间，则a= ．

查看试题解析
15. 如果一个数的平方根是a+6和2a﹣15，则这个数为．

查看试题解析
16. 若 $a = \sqrt{1003} + \sqrt{997}$ ， $b = \sqrt{1001} + \sqrt{999}$ ， $c = 2 \sqrt{1001}$ ，则 $a ， b ， c$ 的大小关系用“＜”号排列为．

查看试题解析

三、解答题（共10题，共72分）

17. 计算： $| \sqrt{3} - 1 | - {(\sqrt{3})}^{2} - 12 \times (- \frac{1}{3})$ ．

查看试题解析
18. 计算： $(- 2)^{2} + | - \sqrt{3} | - \sqrt{25} + (3 - \sqrt{3})^{0}$

查看试题解析
19. 计算： $- (- 2) + (π - 3.14)^{0} - | 1 - \sqrt{3} | + {(- \frac{1}{3})}^{- 1}$

查看试题解析
20. 计算： $\sqrt[3]{- 27} + (- 3)^{0} - \sqrt{8} + | - 2 \sqrt{2} |$ .

查看试题解析
21. 计算： ${(\sqrt{2} - 1)}^{0} + | - 3 | - \sqrt[3]{27} + {(- 1)}^{2021}$ .

查看试题解析
22. 计算： $\sqrt{8} + | \sqrt{3} - 2 | - {(- \frac{1}{2})}^{- 1} + {(π - 2023)}^{0}$ ．

查看试题解析
23. 已知 $5 a + 2$ 的立方根是3， $3 a + b - 1$ 的算术平方根是4，c是 $\sqrt{13}$ 的整数部分．

(1)、求a ， b ， c的值；

(2)、求 $3 a - b + c$ 的平方根．

查看试题解析
24. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} =$ 1 $+ \frac{1}{1} - \frac{1}{2} =$ 1 $\frac{1}{2}$
$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} =$ 1 $+ \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$
$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} =$ 1 $+ \frac{1}{3} - \frac{1}{4} =$ 1 $\frac{1}{12}$
请你根据上面三个等式提供的信息，猜想：

(1)、 $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}} =$

(2)、请你按照上面每个等式反映的规律，写出用n（n为正整数）表示的等式

(3)、利用上述规律计算： $\sqrt{\frac{50}{49} + \frac{1}{64}}$ （份照上式出过程）

查看试题解析
25. 阅读下面的文字，解答问题.
无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来，比如π、 $\sqrt{2}$ 等，而常用“……”或者“≈”的表示方法都不够百分百准确，于是小刚用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小刚的表示方法吗？事实上，小刚的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分，又例如：因为 $\sqrt{4} ＜ \sqrt{5} ＜ \sqrt{9}$ ，即2＜ $\sqrt{5}$ ＜3，所以 $\sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ ，也就是说，任何一个无理数，都可以夹在两个相邻的整数之间。根据上述信息，请回答下列问题：

(1)、 $\sqrt{21}$ 的整数部分是，小数部分是；

(2)、10+ $\sqrt{7}$ 也是夹在两个整数之间的，可以表示为 $a ＜ 10 + \sqrt{7} ＜ b$ ，则 $(a - b)_{}^{2013} =$ ；

(3)、若 $\sqrt{23} - 2 = x + y$ ，其中 $x$ 是整数，且0<y<1，求： $x - y$ 的相反数.

查看试题解析
26. 新定义：若无理数 $\sqrt{T}$ 的被开方数 $T$ （ $T$ 为正整数）满足 $n^{2} < T < (n + 1)^{2}$ （其中 $n$ 为正整数），则称无理数 $\sqrt{T}$ 的“青一区间”为 $(n ， n + 1)$ ；同理规定无理数 $- \sqrt{T}$ 的“青一区间”为 $(- n - 1 ， - n)$ ．例如：因为 $1^{2} < 2 < 2^{2}$ ，所以 $1 < \sqrt{2} < 2$ ，所以 $\sqrt{2}$ 的“青一区间”为 $(1 ， 2)$ ， $- \sqrt{2}$ 的“青一区间”为 $(- 2 ， - 1)$ ．请解答下列问题：

(1)、 $\sqrt{17}$ 的“青一区间”是； $- \sqrt{23}$ 的“青一区间”是；

(2)、若无理数 $- \sqrt{a}$ （ $a$ 为正整数）的“青一区间”为 $(- 3 ， - 2)$ ， $\sqrt{a + 3}$ 的“青一区间”为 $(3 ， 4)$ ，求 $\sqrt[3]{a + 1}$ 的值；

(3)、实数x ， y ， m满足关系式： $\sqrt{2 x + 3 y - m} + \sqrt{3 x + 4 y - 2 m} = \sqrt{x + y - 2023} + \sqrt{2023 - x - y}$ ，求 $m$ 的算术平方根的“青一区间”．

查看试题解析

湘教版数学八年级上册《第3章 实数》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共10题，共72分）

湘教版数学八年级上册《第3章实数》单元提升测试卷