浙教版数学八年级上册《第3章一元一次不等式》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 设“○”“□”“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”"□”“△”按质量从小到大的排列顺序为（）

A、○□△ B、○△□ C、□○△ D、△□○

查看试题解析
2. 已知 $a < b, c < 0$ ，则（）

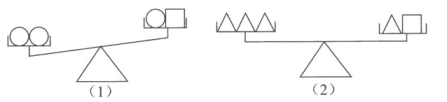A、 $a < b + c$ B、 $a < b - c$ C、 $a c < b c$ D、 $\frac{a}{c} < \frac{b}{c}$

查看试题解析
3. 当0＜x＜1时，x²、x、 $\frac{1}{x}$ 的大小顺序是（　　）

A、x² $< x < \frac{1}{x}$ B、 $\frac{1}{x}$ ＜x＜x² C、 $\frac{1}{x} < x^{2}$ ＜x D、x＜x²＜ $\frac{1}{x}$

查看试题解析
4. 若关于x、y的二元一次方程组 ${\begin{array}{l} x + 3 y = 2 + a \\ 3 x + y = - 4 a \end{array}$ 的解满足x＋y＞2，则a的取值范围为（）

A、a＜−2 B、a＞−2 C、a＜2 D、a＞2

查看试题解析
5. 解不等式组 ${\begin{array}{l} 3 x - 2 < 2 x ① \\ 2 (x + 1) \geq x - 1 ② \end{array}$ 时，不等式①和不等式②的解集在数轴上表示正确的是( )

A、 B、 C、 D、

查看试题解析
6. 若不等式组 ${\begin{array}{l} \frac{x + 1}{3} < \frac{x}{2} - 1 \\ x < 4 m \end{array}$ 无解，则 $m$ 的取值范围为（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m > 2$

查看试题解析
7. 若关于x的不等式组 ${\begin{array}{l} 2 x + 3 > 12 \\ x - a \leq 0 \end{array}$ 恰有3个整数解，则实数a的取值范围是（）

A、 $7 < a < 8$ B、 $7 < a \leq 8$ C、 $7 \leq a < 8$ D、 $7 \leq a \leq 8$

查看试题解析
8. 如图所示为小丽和小欧依序进入电梯时，电梯因超重而警示音响起的过程，且过程中没有其他人进出.
已知当电梯乘载的质量超过 $300 k g$ 时，警示音响起，且小丽、小欧的质量分别为 $50 k g$ 、 $70 k g$ .若小丽进入电梯前，电梯内已乘载的质量为 $x (k g)$ ，则所有满足题意的 $x$ 可用不等式表示为（）

A、 $180 < x ⩽ 250$ B、 $180 < x ⩽ 300$ C、 $230 < x ⩽ 250$ D、 $230 < x ⩽ 300$

查看试题解析
9. 对于任意实数p、q，定义一种运算：p@q＝p-q＋pq，例如2@3＝2-3＋2×3.请根据上述定义解决问题：若关于x的不等式组 ${\begin{array}{l} 2 @ x < 4 \\ x @ 2 \geq m \end{array}$ 有3个整数解，则m的取值范围为是（）

A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-5

查看试题解析
10. 若不等式组 ${\begin{matrix} \end{matrix} \begin{matrix} x + 2 > 2 x - 6 \\ x < m \end{matrix}$ 的解为 $x < 8$ ，则m的取值范围是（）

A、 $m \geq 8$ B、 $m \leq 8$ C、 $m < 8$ D、 $m > 8$

查看试题解析

二、填空题（每题3分，共18分）

11. 某校组织开展了与神舟飞船有关的知识竞赛活动，竞赛试题共有30道，答对一道题得4分，答错或不答一道题扣1分.如果小明想参加本次竞赛且得分不低于80分，那么他至少需要答对道题.

查看试题解析
12. 某同学解一个关于 $x$ 的一元一次不等式 $x - ■ ⩽ 1$ ，不等式中的■是一个数字，但被墨水涂污看不清楚了．根据如图所示的不等式的解集，可知■处的数字为．

查看试题解析
13. 若关于x的不等式 $3 x - 2 m < x - m$ 只有3个正整数解，则m的取值范围是．

查看试题解析
14. 定义一种新运算： $a \otimes b = a - a b$ ，例如： $2 \otimes 3 = 2 - 2 \times 3 = - 4$ ．根据上述定义，不等式组 ${\begin{array}{l} 2 \otimes x \geq - 1 \\ x \otimes 2 \leq 1 \end{array}$ 的整数解为．

查看试题解析
15. 关于 $x$ 的一元一次不等式组 ${\begin{array}{l} 2 x - a \geq 0 \\ b - x < 0 \end{array}$ 的两个不等式的解集在数轴上表示如图，则 $a - b$ 的值为．

查看试题解析
16. 某校决定购买一批篮球和足球共100个。已知篮球和足球的单价分别为120元和90元。根据需求，购买篮球的数量不少于40个。学校可用于购买这批篮球和足球的资金最多为10260元，则有种购买方案。

查看试题解析

三、解答题（共10题，共72分）

17. 解不等式组 $\{\begin{array}{l} 2 x - 6 \leq 0 \\ x < \frac{4 x - 1}{2} \end{array}$ ，并求出它的所有整数解的和．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 5 - x ⩾ 3 (x - 1), \\ \frac{2 x - 1}{3} - \frac{5 x + 1}{2} < 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
19. 解不等式组： ${\begin{array}{l} 2 x + 1 ⩾ x + 2 ① \\ 2 x - 1 < \frac{1}{2} (x + 4) ② \end{array}$ ．

查看试题解析
20. 解不等式组： ${\begin{matrix} 3 x + 6 \geq 5 (x - 2) \\ \frac{x - 5}{2} - \frac{4 x - 3}{3} < 1 \end{matrix}$ ．

查看试题解析
21. 解不等式组： ${\begin{array}{l} 5 x - 2 < 3 (x + 1) (1) \\ \frac{2 x - 2}{3} \geq x - 1 (2) \end{array}$

查看试题解析
22. 解不等式组 ${\begin{matrix} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{matrix}$

查看试题解析
23. 某班为了丰富学生的课外活动和体育健身，计划购买10个足球和20根跳绳，共花费980元，其中足球的价格是跳绳价格的3倍多8元．

(1)、求跳绳和足球的单价；

(2)、在实际课外活动中，发现如果全班同学根据自身的爱好总有部分学生无法玩足球或跳绳，若使用剩余班费233元，并要求至少购买一个足球，那么最多可购买多少根跳绳？

查看试题解析
24. 上周末，小马约上小唐一起出发去离学校 $240 km$ 的 $A$ 地游玩，小唐从学校出发，半小时后、小马也从学校出发，已知小唐的车速是小马的车速的 $\frac{3}{4}$ ，结果小马比小唐提前 $18$ 分钟到达 $A$ 地．

(1)、求小马和小唐的车速分别为多少？（单位：千米 $/$ 小时）

(2)、 $A$ 地游玩之后，小马和小唐两车以原速度同时出发前往 $B$ 地，小马的车行驶了 $2$ 小时后发生故障，小马原地检修用了 $20$ 分钟后以原速度的 $80 %$ 行驶．此时，小唐提高速度，为了保证小唐再用不超过1小时与小马相遇，那么小唐的行驶速度至少提高多少千米小时？

查看试题解析
25. 五一假期，某旅行团32人在秦王宫景区游玩，他们由成人和儿童组成.已知成人比儿童多12人.

(1)、求该旅行团中成人与儿童分别是多少人？

(2)、因时间充裕，该团准备让部分成人带领全部儿童去清明上河图景区游玩，清明上河图景区的门票价格为160元/张，成人全票，儿童5折，一名成人可以免费携带一名儿童.并且为安全起见，一个成人最多监护两个儿童.
①若由成人8人带队，则所需门票的总费用是多少元？

②若剩余经费只有1400元可用于购票，在不超额的前提下，可以安排多少成人带队？求所有满足条件的方案.

查看试题解析
26. 阅读下列材料：
解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法：
解：∵x﹣y=2，又∵x＞1，∴y+2＞1，即y＞﹣1
又y＜0，∴﹣1＜y＜0．…①
同理得：1＜x＜2．…②
由①+②得﹣1+1＜y+x＜0+2，∴x+y的取值范围是0＜x+y＜2．
请按照上述方法，完成下列问题：
已知关于x、y的方程组 ${\begin{matrix} 2 x - y = - 1 \\ x + 2 y = 5 a - 8 \end{matrix}$ 的解都为非负数．

(1)、求a的取值范围；

(2)、已知2a﹣b=1，且，求a+b的取值范围；

(3)、已知a﹣b=m（m是大于1的常数），且b≤1，求2a+b最大值．（用含m的代数式表示）

查看试题解析

浙教版数学八年级上册《 第3章 一元一次不等式》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共10题，共72分）

浙教版数学八年级上册《第3章一元一次不等式》单元提升测试卷