浙教版数学九年级上册《第3章圆的基本性质》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是：在工件圆弧上任取两点A ， B ，连接AB ，作AB的垂直平分线CD交AB于点D ，交 $\hat{A B}$ 于点C ，测出AB＝40cm ， CD＝10cm ，则圆形工件的半径为（　　）

A、50cm B、35cm C、25cm D、20cm

查看试题解析
2. 如图，在⊙O中，弦AB⊥弦CD，垂足为E，若AE=2， BE=6， DE=3，则⊙O的面积是（）

A、20π B、13π C、 $\frac{65}{4} π$ D、 $\frac{11}{4} π$

查看试题解析
3. 如图，A、B、C、P是 $⊙ O$ 上的四个点， $∠ A C B = 60 °$ ，且 $P C$ 平分 $∠ A P B$ ，则 $△ A B C$ 的形状是（　　）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
4. 如图，AB是⊙O的弦，OC⊥AB交⊙O于点C ，点D是⊙O上一点，连接BD ， CD ．若∠D＝28°，则∠OAB的度数为（　　）

A、28° B、34° C、56° D、62°

查看试题解析
5. 如图，△ABC内接于⊙O，DE，FG是⊙O的弦，AB＝DE，FG＝AC．下列结论：①DE+FG＝BC；② $\overset{⌢}{D E}$ + $\overset{⌢}{F G}$ ＝ $\overset{⌢}{B C}$ ；③∠DOE+∠FOG＝∠BOC；④∠DEO+∠FGO＝∠BAC．其中所有正确结论的序号是（）

A、①②③④ B、②③ C、②④ D、②③④

查看试题解析
6. 如图，半圆 $O$ 的直径 $A B = 6$ ，两弦 $A C 、 B D$ 相交于点 $E$ ，弦 $C D = 3$ ，则 $∠ C B D$ 等于（）

A、 $22.5 °$ B、 $30 °$ C、 $36 °$ D、 $45 °$

查看试题解析
7. 如图，AB是 $⊙ O$ 的直径，C，D是 $⊙ O$ 上的两点，连接AC，CD，AD，若 $∠ A D C = 75 °$ ，则 $∠ B A C$ 的度数是（）

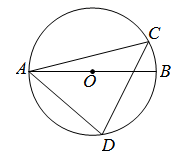A、15° B、25° C、30° D、75°

查看试题解析
8. 如图，四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，若∠BEC＝20°，则∠ADC的度数为（）

A、100° B、110° C、120° D、130°

查看试题解析
9. 如图，在扇形AOB中，∠AOB＝80°，半径OA＝3，C是 $\overset{⌢}{A B}$ 上一点，连接OC ， D是OC上一点，且OD＝DC ，连接BD ．若BD⊥OC ，则 $\overset{⌢}{A C}$ 的长为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、π

查看试题解析
10. 如图，在矩形 $A B C D$ 中，分别以点A和C为圆心，AD长为半径画弧，两弧有且仅有一个公共点.若 $A D = 4$ ，则图中阴影部分的面积为( )

A、 $32 - 8 π$ B、 $16 \sqrt{3} - 4 π$ C、 $32 - 4 π$ D、 $16 \sqrt{3} - 8 π$

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，在⊙O中，直径AB⊥CD于点E ， CD＝6，BE＝1，则弦AC的长为．

查看试题解析
12. 某新建学校因场地限制，要合理规划体育场地．小明绘制的铅球场地设计图如图所示，该场地由⊙O和扇形OBC组成，OB ， OC分别与⊙O交于点A ， D ． OA＝1m ， OB＝10m ， ∠AOD＝40°，则阴影部分的面积为m²（结果保留π）．

查看试题解析
13. 如图，在 $⊙ O$ 中， $\overset{⏜}{A B} = \overset{⏜}{C D}$ ，则下列结论中： $① A B = C D$ ； $② A C = B D$ ； $③ ∠ A O C = ∠ B O D$ ； $④ \overset{⏜}{A C} = \overset{⏜}{B D}$ ，正确的是 $($ 填序号 $)$ ．

查看试题解析
14. 如图，AB是圆的直径， $∠ 1 、 ∠ 2 、 ∠ 3 、 ∠ 4$ 的顶点均在AB上方的圆弧上， $∠ 1 、 ∠ 4$ 的一边分别经过点A、B，则 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 =$ .

查看试题解析
15. 如图，四边形ABCD内接于 $⊙ O$ ，延长AD至点 $E$ ，已知 $∠ A O C = 14 0^{°}$ ，那么 $∠ C D E =$ °.

查看试题解析
16. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $A C = \sqrt{3}$ ，以 $C$ 为圆心， $C A$ 为半径的圆弧分别交 $A B$ 、 $C B$ 于点 $D$ 、 $E$ ，则图中阴影部分面积之和为．

查看试题解析

三、解答题（共8题，共72分）

17. 石拱桥是我国古代人民勤劳和智慧的结晶（如图①），赵州桥是我国古代石拱桥的代表，图②是根据该石拱桥画出的几何图形，桥的主桥拱是圆弧形，表示为 $\overset{⌢}{A B}$ ，桥的跨度（弧所对的弦长） $A B = 30 m$ ，设 $\overset{⌢}{A B}$ 所在圆的圆心为O ， $O B$ ， $O C$ 为半径，半径 $O C ⊥ A B$ ，垂足为D.拱高（弧的中点到弦的距离） $C D = 5 m$ ．

(1)、直接写出 $A D$ 与 $B D$ 的数量关系；

(2)、求这座石拱桥主桥拱的半径．

查看试题解析
18. 如图， $A B$ 是 $⊙ O$ 的弦，半径 $O D ⊥ A B$ ，垂足为 $C$ ，点 $E$ 在 $⊙ O$ 上，连接 $O A$ ， $D E$ ， $B E$ ．

(1)、若 $∠ D E B = 30 °$ ，求 $∠ A O D$ 的度数；

(2)、若 $C D = 2$ ， $A B = 8$ ，求 $⊙ O$ 的半径长．

查看试题解析
19. 如图，在正方形 $A B C D$ 中有一点P ，连接 $A P$ 、 $B P$ ，旋转 $△ A P B$ 到 $△ C E B$ 的位置．

(1)、若正方形的边长是8， $B P = 4$ ．求阴影部分面积；

(2)、若 $B P = 4$ ， $A P = 7$ ， $∠ A P B = 135 °$ ，求 $P C$ 的长．

查看试题解析
20. 如图，AB是 $⊙ O$ 的直径， $C D = C B$ ， $C E ⊥ A B$ 于点E ，连接BD交CE于点F.

(1)、求证： $C F = B F$ .

(2)、若 $C D = 4 \sqrt{5}$ ， $A C = 8 \sqrt{5}$ ，求弦BD的长.

查看试题解析
21. 如图，⊙O半径为2，弦BC=3，A是弦BC所对优弧上的一个点，连结CO并延长交⊙O于点M，连结AM，过点B作BE⊥AC，垂足为E.

(1)、求证：BE//AM.

(2)、过点A作AD⊥BC，分别交BE，BC于点H，D.求AH的长.

查看试题解析
22. 如图， $O A ， O B ， O C$ 都是 $⊙ O$ 的半径， $∠ A C B = 2 ∠ B A C$ ．

(1)、求证： $∠ A O B = 2 ∠ B O C$ ；

(2)、若 $A B = 4 ， B C = \sqrt{5}$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 如图，四边形ABCD内接于⊙O，C是 $\overset{⏜}{B D}$ 的中点，延长AB至点E，使得BE=AD，连结AC，CE.

(1)、求证：AC=CE.

(2)、若AD=4 $\sqrt{3}$ ， AB=6 $\sqrt{3}$ ， ∠BCD=120°，求BC的长。

查看试题解析
24. 【实际情境】
手工课堂上，老师给每个制作小组发放一把花折伞和制作花折伞的材料及工具.同学们认真观察后，组装了花折伞的骨架，粘贴了彩色伞面，制作出精美的花折伞.

(1)、【模型建立】
如图1，从花折伞中抽象出“伞形图”. $A M = A N$ ， $D M = D N$ .求证： $∠ A M D = ∠ A N D$ .

(2)、【模型应用】
如图2， $△ A M C$ 中， $∠ M A C$ 的平分线 $A D$ 交 $M C$ 于点D.请你从以下两个条件：
① $∠ A M D = 2 ∠ C$ ；② $A C = A M + M D$ 中选择一个作为已知条件，另一个作为结论，并写出结论成立的证明过程.（注：只需选择一种情况作答）

(3)、【拓展提升】
如图3， $A C$ 为 $⊙ O$ 的直径， $\overset{⌢}{A B} = \overset{⌢}{B C}$ ， $∠ B A C$ 的平分线 $A D$ 交 $B C$ 于点E ，交 $⊙ O$ 于点D ，连接 $C D$ .求证： $A E = 2 C D$ .

查看试题解析

浙教版数学九年级上册《第3章 圆的基本性质》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

浙教版数学九年级上册《第3章圆的基本性质》单元提升测试卷