北师大版数学八年级上册《第三章位置与坐标》单元提升测试卷

试卷更新日期：2024-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，小明从点 $O$ 出发，先向西走 $400 m$ ，再向南走 $300 m$ 到达点 $M$ ，如果点 $M$ 的位置用 $(- 4 ， - 3)$ 表示，那么 $(1 ， - 2)$ 表示的位置是（）

A、点A B、点B C、点C D、点D

查看试题解析
2.
周末，小明与小文相约一起到游乐园去游玩，如图是他俩在微信中的一段对话：
根据上面两人的对话纪录，小文能从M超市走到游乐园门口的路线是（　　）

A、向北直走700米，再向西直走300米 B、向北直走300米，再向西直走700米 C、向北直走500米，再向西直走200米 D、向南直走500米，再向西直走200米

查看试题解析
3. 已知点 $A (a ， b)$ ，其中a ， b均为实数，若a ， b满足 $3 a = 2 b + 5$ ，则称点A为“和谐点”.若点 $B (k + 2 ， 1 - \frac{1}{2} k)$ 是“和谐点”，则点B在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知点 $P (x ， y)$ 在第四象限，且 $| x | = 3 ， | y | = 5$ ，则 $P$ 点的坐标是（）

A、 $(- 3 ， - 5)$ B、 $(5 ， - 3)$ C、 $(3 ， - 5)$ D、 $(- 3 ， 5)$

查看试题解析
5. 已知点A的坐标为（1，2），直线AB∥x轴，且AB＝5，则点B的坐标为（）

A、（5，2）或（4，2） B、（6，2）或（-4，2） C、（6，2）或（－5，2） D、（1，7）或（1，－3）

查看试题解析
6. 如图，动点 $P$ 在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点 $(- 1 ， 1)$ ，第2次接着运动到点 $(- 2 ， 0)$ ，第3次接着运动到点 $(- 3.2)$ ， ……，按这样的运动规律，经过第2025次运动后，动点 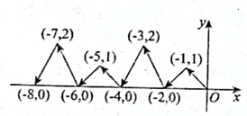$P$ 的坐标是（）．

A、 $(- 2025 ， 0)$ B、 $(- 2025 ， 1)$ C、 $(- 2025 ， 2)$ D、 $(- 2026 ， 1)$

查看试题解析
7. 若点 $A (x ， 1)$ 与 $B (- 2 ， y)$ 关于 $x$ 轴对称，则（）．

A、 $x = - 2$ ， $y = 1$ B、 $x = - 2$ ， $y = - 1$ C、 $x = 2$ ， $y = - 1$ D、 $x = 2$ ， $y = 1$

查看试题解析
8. 在平面直角坐标系中，若干个边长为 $2$ 个单位长度的等边三角形，按如图中的规律摆放 $.$ 点 $P$ 从原点 $O$ 出发，以每秒 $2$ 个单位长度的速度沿着等边三角形的边“ $O A_{1} \to A_{1} A_{2} \to A_{2} A_{3} \to A_{3} A_{4} \to A_{4} A_{5} \dots$ ”的路线运动，设第 $n$ 秒点 $P$ 运动到点 $P_{n} (n$ 为正整数 $)$ ，则点 $P_{2023}$ 的坐标是（）

A、 $(- 2022，0)$ B、 $(- 2023 ， - \sqrt{3})$ C、 $(- 2022 ， \sqrt{3})$ D、 $(- 2023 ， \sqrt{3})$

查看试题解析
9. 已知点 $P (2 m + 3 n ， 2)$ 与点 $Q (6 ， 3 m - 2 n)$ 关于x轴对称，在 $△ A B C$ 中，边 $A B$ ， $A C$ 的垂直平分线分别交 $B C$ 于点M ， G（如图），连 $A M$ ， $A G$ ．若 $B C = 26 m + 13 n$ ．则 $△ A M G$ 的周长为（）

A、28 B、30 C、32 D、34

查看试题解析
10. 如图，弹性小球从点 $P (0 ， 1)$ 出发，沿所示方向运动，每当小球碰到正方形 $O A B C$ 的边时反弹，反弹时反射角等于入射角，当小球第1次碰到正方形的边时的点为 $P_{1} (2 ， 0)$ ，第2次碰到正方形的边时的点为 $P_{2}$ ， …，第 $n$ 次碰到正方形的边时的点为 $P_{n}$ ，则点 $P_{2024}$ 的坐标是（）

A、 $(2 ， 0)$ B、 $(4 ， 3)$ C、 $(2 ， 4)$ D、 $\begin{array}{l} (4 ， 1) \end{array}$

查看试题解析

二、填空题（每题3分，共18分）

11. 在平面直角坐标系中，若点 $P (m + 3 ， 3 - m)$ 在y轴上，则m的值是.

查看试题解析
12. 如图，所有正方形的中心均在坐标原点，且各边与坐标轴平行，从内到外，它们的边长依次为2，4，6，8，…，顶点依次为 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $A_{4}$ ， …，则顶点 $A_{2024}$ 的坐标是．

查看试题解析
13. 在平面直角坐标系中，点 $A (3 a - 5 ， a + 1)$ 在第二象限，且该点到 $x$ 轴与到 $y$ 轴的距离相等，则 $A$ 点坐标为．

查看试题解析
14. 如图，在平面直角坐标系中，点 $A$ 的坐标是 $(- 3 ， 0)$ ，点 $B$ 的坐标是 $(0 ， 4)$ ，点 $C$ 是 $O B$ 上一点，将 $△ A B C$ 沿 $A C$ 折叠，点 $B$ 恰好落在 $x$ 轴上的点 $B^{'}$ 处，则点 $C$ 的坐标为．

查看试题解析
15. 如图，在平面直角坐标系中．对 $△ A B C$ 进行循环往复的轴对称变换，若原来点A坐标是 $(a ， b)$ ，则经过第2023次变换后所得的A点坐标是．

查看试题解析
16. 如图，在平面直角坐标系中，△ABC关于直线m对称，直线m与x轴交点为(1，0)，点C的坐标为(4，1)，则点B的坐标为.

查看试题解析

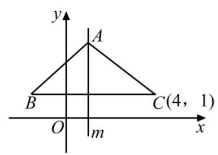
三、解答题（共8题，共72分）

17. 已知△ABC在平面直角坐标系中的位置如图所示，A，B，C三点均在格点上.

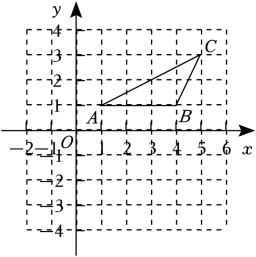(1)、在直角坐标系内画出△ABC关于x轴对称的△A'B'C'，并写出点A'，B'，C'的坐标；

(2)、若点P与点C关于y轴对称，则点P的坐标为；

(3)、如果要使△ABD与△ABC全等，那么点D的坐标是.

查看试题解析
18. 已知点P(2x- 6，3x+1)，求下列情形下点P的坐标．

(1)、点P在y轴上．

(2)、点P到y轴的距离为6．

(3)、点P在过点A(2，-4)且与y轴平行的直线上．

查看试题解析
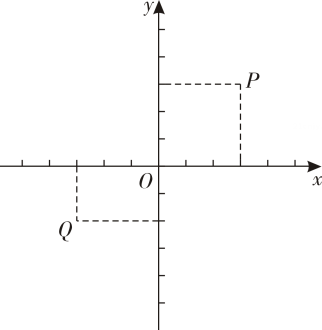
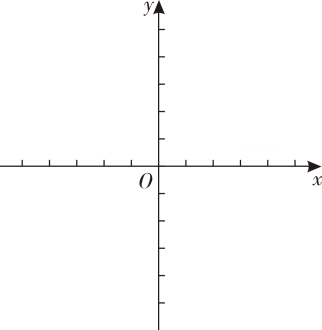
19. 在平面直角坐标系 $x O y$ 中，对于 $P$ ， $Q$ 两点给出如下定义：若点 $P$ 到 $x$ 、 $y$ 轴的距离中的最大值等于点 $Q$ 到 $x$ 、 $y$ 轴的距离中的最大值，则称 $P$ ， $Q$ 两点为“等距点”．如图中的 $P$ ， $Q$ 两点即为“等距点”．
备用图

(1)、已知点 $A$ 的坐标为 $(- 3 ， 1)$ ，在点 $E (0 ， 3)$ ， $F (3 ， - 3)$ ， $G (2 ， - 5)$ 中，为点 $A$ 的“等距点”的是．

(2)、若 $T_{1} (- 1 ， - k - 3)$ ， $T_{2} (4 ， 4 k - 3)$ 两点为“等距点”，且两点纵坐标异号，求 $k$ 的值．

查看试题解析
20. 如图，在直角坐标系中，已知点 $A (1 ， 2) ， B (- 1 ， 3) ， C (2.5 ， - 1)$ ，直线l是第二、四象限的角平分线．

(1)、操作：连结线段 $A B$ ，作出线段 $A B$ 关于直线l的轴对称图形 $A_{1} B_{1}$ ．

(2)、发现：请写出坐标平面内任一点 $P (a ， b)$ 关于直线l的对称点 $P^{'}$ 的坐标．

(3)、应用：请在直线l上找一点Q，使得 $Q A + Q C$ 最小，并写出点Q的坐标．

查看试题解析
21. 已知当 $m$ 、 $n$ 都是实数，且满足 $2 m = 6 + n$ ，则称点 $A (m - 1 ， \frac{n}{2})$ 为“智慧点”．

(1)、判断点 $P (4 ， 10)$ 是否为“智慧点”，并说明理由．

(2)、若点 $M (a ， 1 - 2 a)$ 是“智慧点”．请判断点 $M$ 在第几象限？并说明理由．

查看试题解析
22. 如图所示的象棋棋盘上，若帅位于点（1，0）上，相位于点（3，0）上.

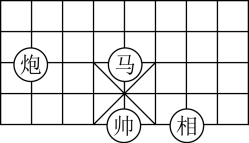(1)、请在如图所示的网格中建立平面直角坐标系；

(2)、炮所在点的坐标是，马与帅的距离是；

(3)、若要把炮移动到与它关于y轴对称的点的位置，则移动后炮的位置是（用坐标表示）.

查看试题解析
23. 定义：在平面直角坐标系中，对于任意两点 $A (a ， b)$ ， $B (c ， d)$ ，若点 $T (x ， y)$ 满足 $x = \frac{a + c}{3}$ ， $y = \frac{b + d}{3}$ ，那么称点 $T$ 是点 $A$ 和 $B$ 的衍生点.例如： $M (- 2 ， 5)$ ， $N (8 ， - 2)$ ，则点 $T (2 ， 1)$ 是点 $M$ 和 $N$ 的衍生点.已知点 $D (3 ， 0)$ ，点 $E (m ， m + 2)$ ，点 $T (x ， y)$ 是点 $D$ 和 $E$ 的衍生点.

(1)、若点 $E (4 ， 6)$ ，则点 $T$ 的坐标为

(2)、请直接写出点 $T$ 的坐标（用 $m$ 表示）；

(3)、若直线 $E T$ 交 $x$ 轴于点 $H$ ，当 $∠ D H T = 90 °$ 时，求点 $E$ 的坐标.

查看试题解析
24. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，线段 $D E$ 经过点C，且 $A D ⊥ D E$ 于点D， $B E ⊥ D E$ 于点E．求证： $A D = C E$ ， $C D = B E$ ”这个问题时，只要证明 $△ A D C ≌ △ C E B$ ，即可得到解决，

(1)、积累经验：
请写出证明过程；

(2)、类比应用：
如图2，在平面直角坐标系中， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点A的坐标为 $(0 ， 2)$ ，点C的坐标为 $(1 ， 0)$ ，求点B与x轴的距离．

(3)、拓展提升：
如图3， $△ A B C$ 在平面直角坐标系中， $∠ A C B = 90 °$ ， $A C = B C$ ，点A的坐标为 $(2 ， 1)$ ，点C的坐标为 $(4 ， 2)$ ，求点B的坐标．

查看试题解析

北师大版数学八年级上册《第三章 位置与坐标》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学八年级上册《第三章位置与坐标》单元提升测试卷