江西省萍乡市2023-2024学年七年级下学期期末数学试题

试卷更新日期：2024-08-08 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题只有一个正确选项）

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $3 x^{2} + 4 x^{2} = 7 x^{4}$ B、 $2 x^{2} \cdot 3 x^{2} = 6 x^{2}$ C、 $x \div x^{- 2} = x^{3}$ D、 ${(- \frac{1}{2} x^{2} y)}^{3} = - \frac{1}{6} x^{6} y^{3}$

查看试题解析
3. 人体内的淋巴细胞直径约是0.0000051米，将0.0000051用科学记数法表示为（）

A、 $0.51 \times 1 0^{- 5}$ B、 $5.1 \times 1 0^{5}$ C、 $5.1 \times 1 0^{- 6}$ D、 $0.51 \times 1 0^{6}$

查看试题解析
4. 下列事件中，是必然事件的是（）

A、内错角相等 B、掷两枚硬币，必有一个正面朝上，一个反面朝上 C、13人中至少有两个人的生肖相同 D、打开电视，一定能看到新闻联播

查看试题解析
5. 设 $x^{2} + m x + 4$ 是一个完全平方式，那么 $m$ 的值是（）

A、4 B、 $\pm 4$ C、 $\pm 2$ D、 $- 2$

查看试题解析
6. 如图，已知直线 $A B / / C D$ ， $∠ C = 125 °$ ， $∠ A = 45 °$ ，那么 $∠ E$ 的大小为（）

A、80° B、70° C、90° D、100°

查看试题解析
7. 如图，已知 $∠ A C B = 90 °$ ， $B C = 8$ ， $A C = 6$ ， $A B = 10$ ，点 $D$ 在线段AB上运动，线段CD的最短距离是（）

A、4.8 B、4 C、5.8 D、5

查看试题解析
8. 已知等腰 $△ A B C$ 中， $∠ A = 40 °$ ，则底角的大小为（）

A、40° B、70° C、100° D、40°或70°

查看试题解析
9. 如图所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后走路回家，中途去早餐店吃早餐，然后接着走回家，其中x表示时间，y表示张强离家的距离.根据图象提供的信息，以下四个说法中错误的有（）

A、体育场离张强家3.5千米 B、张强在体育场锻炼了15分钟 C、体育场离早餐店1.5千米 D、张强从早餐店回家的平均速度是3千米/小时

查看试题解析
10. 已知：如图，在长方形 $A B C D$ 中， $A B = 4$ ， $A D = 6$ ，延长BC到点E ，使 $C E = 2$ ，连接DE ，动点P从点B出发，以每秒2个单位的速度沿 $B C \to C D \to D A$ 向终点A运动，设点P的运动时间为t秒，当 $△ A B P$ 和 $△ D C E$ 全等时，t的值为（）

A、1 B、1或3 C、1或7 D、3或7

查看试题解析

二、填空题（本大题共8个小题，每小题3分，共24分，请把答案填在答题卡上）

11. ${(- 2 a b^{2})}^{3} =$ .

查看试题解析
12. 若 $m^{2} - n^{2} = 6$ ， $m - n = 3$ ，则 $m + n =$ .

查看试题解析
13. 在等腰 $△ A B C$ 中，如果两边长分别为5、10，则第三边的长为.

查看试题解析
14. 如 $(x + m)$ 与 $(x - 3)$ 的乘积中不含 $x$ 的一次项，则 $m$ 的值为.

查看试题解析
15. 如图，用一段长为20米的篱笆围成一个一边靠墙（墙的长度不限）的长方形菜园 $A B C D$ ，设AB为x米，则菜园的面积y（平方米）与x（米）的关系式为.（不写x的取值范围）

查看试题解析
16. 一枚质地均匀的正方体骰子，其六个面上分别刻有1，2，3，4，5，6六个数字，抛掷这枚骰子一次，则向上的面的数字大于4的概率是.

查看试题解析
17. 如图有一张直角三角形纸片，两直角边AC＝4cm ， BC＝8cm ，把纸片的部分折叠，使点B与点A重合，折痕为DE ，则△ACD的周长为．

查看试题解析
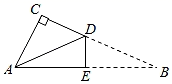18. 已知，如图 $△ A B C$ ，点D是 $△ A B C$ 内一点，连接BD ， CD ，则 $∠ B D C$ 与 $∠ A$ ， $∠ 1$ ， $∠ 2$ 之间的数量关系为.

查看试题解析

三、解答题（本大题共3小题，第19题8分，第20题4分，第21题5分，共17分）

19.

(1)、计算： $- 3^{2} + 5^{0} + | - 2 |$

(2)、先化简，再求值： $(2 a + b) (2 a - b) - 3 (a + b)^{2} + 4 b^{2}$ ，其中 $a = 2$ ， $b = - 1$ .

查看试题解析
20. 下列正方形网格图中，部分方格涂上了阴影，请按不同要求作图.

(1)、如图①，将某一个方格涂上阴影，使整个图形有两条对称轴；

(2)、如图②，将某一个方格涂上阴影，使整个图形有四条对称轴.

查看试题解析
21. 如图， $∠ A B C = ∠ B C D$ ，若 $∠ A = ∠ D$ ，试说明： $A E / / B D$ .

查看试题解析

四、解答题（本大题共2小题，每小题各5分，共10分）

22. 端午节期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图，转盘被等分成8个扇形）.如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中纪念奖，指向其余数字不中奖.

(1)、转动转盘中奖的概率是多少？

(2)、端午节期间有1000人参与这项活动，估计获得一等奖的人数是多少？

查看试题解析
23. 如图，在 $△ A B C$ 中，BD是AC边上的高线，点P在边BC上，连接DP ， $∠ B D P + ∠ A = 90 °$ .

(1)、请判断DP与AB的位置关系，并说明理由；

(2)、若BD平分 $∠ A B C$ ， $∠ A = 67 °$ ，求 $∠ B P D$ 的度数.

查看试题解析

五、解答题（本大题共2小题，每小题各6分，共12分）

24. 如图，在 $△ A B C$ 与 $△ D E F$ 中，点B ， E ， C ， F在一条直线上， $A B / / D E$ ， $A C = D F$ ， $∠ A = ∠ D$ .

(1)、试说明 $△ A B C ≌ △ D E F$ ；

(2)、若 $B F = 7$ ， $C E = 3$ ，求线段BE的长度.

查看试题解析
25. 如图（1），B地在A地的正东方向，某一时刻，乙车从B地开往A地，1小时后，甲车从A地开往B地，当甲车到达B地的同时乙车也到达A地.如图（2），横轴x（小时）表示两车的行驶时间（从乙车出发的时刻开始计时），纵轴y（千米）表示两车与A地的距离.

问题：

(1)、A、B两地相距千米；

(2)、 $l_{1}$ 和 $l_{2}$ 两段线分别表示两车距A地的距离y（千米）与行驶时间x（小时）之间的关系，请问：表示甲车的图象为，表示乙车的图象为；

(3)、求两车相遇时距A地多少千米？

查看试题解析

六、解答题（本大题共1小题，共7分）

26. 已知点A、D在直线l的同侧.

(1)、如图1，在直线l上找一点C ，使得线段 $A C + D C$ 最小（请通过画图指出点C的位置）；

(2)、如图2，在直线l上取两点B、E ，恰好能使 $△ A B C$ 和 $△ C D E$ 均为等边三角形，M、N分别是线段AC、BC上的动点，连接DN交AC于点G ，连接EM交CD于点F.
①当点M、N分别是AC、BC的中点时，判断线段EM与线段DN的数量关系，并说明理由；
②如图3，若点M、N分别从点A和B开始沿线段AC和线段BC以相同的速度向点C匀速运动，当M、N与点C重合时运动停止，判断在运动过程中线段GF与直线l的位置关系.

查看试题解析