广东省珠海市金湾区2023-2024学年七年级下学期期末考试数学试题
试卷更新日期:2024-08-08 类型:期末考试
一、选择题:本大题共10小题,每小题3分,共30分.每小题给出的四个选项中只有一项是符合题目要求的.
-
1. 下列数中是无理数的是 ( )A、 B、-1 C、 D、π2. 下列调查中,最适合采用全面调查的是 ( ).A、检测某市的空气质量 B、对旅客上飞机前的安检 C、了解一批节能灯泡的使用寿命 D、对五一节假日期间居民出行方式的调查3. 在平面直角坐标系中,点A(-4,3)所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 我区年八年级“国家体质健康测试”中,立定跳远为必测项目,如图为测量立定跳远成绩的示意图,其依据的数学原理是( )
 A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过一点有且只有一条直线与已知直线垂直5. 若a<b,则下列各式一定成立的是 ( ).A、a-1<b-1 B、 C、 D、ac<bc6. 不等式组的解集在数轴上表示,正确的是( )A、
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过一点有且只有一条直线与已知直线垂直5. 若a<b,则下列各式一定成立的是 ( ).A、a-1<b-1 B、 C、 D、ac<bc6. 不等式组的解集在数轴上表示,正确的是( )A、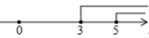 B、
B、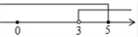 C、
C、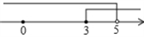 D、
D、 7. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图是一局象棋残局,已知表示棋子“馬”和“車”的点坐标分别为(4,3),(-2, 1), 则表示棋子“炮”的点坐标为( ).
7. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图是一局象棋残局,已知表示棋子“馬”和“車”的点坐标分别为(4,3),(-2, 1), 则表示棋子“炮”的点坐标为( ). A、(2, 3) B、(2, 1) C、(1, 2) D、(1, 3)8. 如图,光在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.在空气中平行的两条入射光线,在水中的两条折射光线也是平行的,若水面和杯底互相平行,且 , 则的度数为( )
A、(2, 3) B、(2, 1) C、(1, 2) D、(1, 3)8. 如图,光在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.在空气中平行的两条入射光线,在水中的两条折射光线也是平行的,若水面和杯底互相平行,且 , 则的度数为( ) A、 B、 C、 D、9. 长跑比赛中,张华跑在前面,在离终点 100m时他以4m/s的速度向终点冲刺,在他身后10m的李明需以多快的速度同时开始冲刺,才能够在张华之前到达终点?设李明冲刺的速度为xm/s,可列出不等式为 ( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,长方形ADCB的边 BC平行于x轴,如果点A 的坐标为(-1,2), 点C的坐标为(3,-3),把一根长为2024个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A 处,并按顺时针方向绕在长方形 ADCB的边上,则细线的另一端所在位置的坐标为( ).
A、 B、 C、 D、9. 长跑比赛中,张华跑在前面,在离终点 100m时他以4m/s的速度向终点冲刺,在他身后10m的李明需以多快的速度同时开始冲刺,才能够在张华之前到达终点?设李明冲刺的速度为xm/s,可列出不等式为 ( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,长方形ADCB的边 BC平行于x轴,如果点A 的坐标为(-1,2), 点C的坐标为(3,-3),把一根长为2024个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A 处,并按顺时针方向绕在长方形 ADCB的边上,则细线的另一端所在位置的坐标为( ). A、(3, -2) B、(3, -3) C、(2, -3) D、(2, 2)
A、(3, -2) B、(3, -3) C、(2, -3) D、(2, 2)二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 把方程 改写成用含y的式子表示x的形式,则. .12. 如图,根据机器零件的设计图纸,用不等式表示零件长度的合格尺寸(L的取值范围)为.
 13. 在七年级的一次考试中,1班某道单项选择题的作答情况如图所示,由统计图可得选C的人数是人.
13. 在七年级的一次考试中,1班某道单项选择题的作答情况如图所示,由统计图可得选C的人数是人. 14. 已知 是关于x、y的二元一次方程ax+by=3的一组解, 则代数式4a+2b-2的值为.15. 如图1是长方形纸带, ∠DEF=25°, 将纸带沿EF折叠成图2,再沿BF折叠成图3, 则图3中的∠CFE 的度数是.
14. 已知 是关于x、y的二元一次方程ax+by=3的一组解, 则代数式4a+2b-2的值为.15. 如图1是长方形纸带, ∠DEF=25°, 将纸带沿EF折叠成图2,再沿BF折叠成图3, 则图3中的∠CFE 的度数是.
三、解答题 (一) :本大题共4小题, 每小题6分, 共24分.
-
16. 计算:17. 解方程组18. 如图,在四边形中,E是上一点,延长交延长线于点F, , . 求证: .
 19. 如图,把两张小正方形纸片分别沿对角线剪开,拼成一张面积为 的大正方形纸片.
19. 如图,把两张小正方形纸片分别沿对角线剪开,拼成一张面积为 的大正方形纸片. (1)、小正方形纸片的边长为cm;(2)、若沿此大正方形纸片边的方向剪出一张长方形纸片,能否使剪出的长方形纸片的长宽之比为2∶1,且面积为 若能,试求出剪出的长方形纸片的长和宽;若不能,请说明理由.
(1)、小正方形纸片的边长为cm;(2)、若沿此大正方形纸片边的方向剪出一张长方形纸片,能否使剪出的长方形纸片的长宽之比为2∶1,且面积为 若能,试求出剪出的长方形纸片的长和宽;若不能,请说明理由.四、解答题 (二) :本大题共3小题, 每小题9分, 共27分.
-
20. 如图,三角形ABC三个顶点坐标分别为A(3, 4), B(1,3) , C(4, 1), 点A'的坐标为(-2, 3) .
 (1)、 将三角形ABC平移, 使点A与点 重合,画出平移后的三角形.(2)、 点B'的坐标为 , 点C'的坐标为 ;(3)、 连接OB, 在x轴上找点D, 使 的面积是 面积的2倍,直接写出点 D的坐标.21. 某中学开展专家讲座,帮助学生合理规划周末使用手机的时间,并在讲座前后对本校学生周末手机使用时间情况进行随机抽样调查,制成如下统计图表(数据分组包含左端值不包含右端值).
(1)、 将三角形ABC平移, 使点A与点 重合,画出平移后的三角形.(2)、 点B'的坐标为 , 点C'的坐标为 ;(3)、 连接OB, 在x轴上找点D, 使 的面积是 面积的2倍,直接写出点 D的坐标.21. 某中学开展专家讲座,帮助学生合理规划周末使用手机的时间,并在讲座前后对本校学生周末手机使用时间情况进行随机抽样调查,制成如下统计图表(数据分组包含左端值不包含右端值).
讲座开展前学生周末手机使用时间
人数
0~2小时
5
2~4小时
8
4~6小时
15
6~8小时
12
8小时以上
10
(1)、在讲座开展前抽取的学生中周末使用时长在哪个区间的人数最多?占抽取人数的百分之几?(2)、该校共有学生1500人,请估计讲座开展后全校周末使用手机8小时以上的学生人数;(3)、小军认为,讲座开展后的样本中周末使用手机6小时以上的人数与讲座开展前相比变化不大,所以讲座并没有起到效果.请结合统计图表,对小军分析数据的方法及讲座宣传活动的效果谈谈你的看法.22. 古人曰:“读万卷书,行万里路”,七年级同学开启了期盼已久的研学活动,师生一起去参观珠海博物馆.下面是王老师和小真、小萱同学有关租车问题的对话:王老师:“客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45 座的贵 200 元. ”
小真:“八年级师生昨天在这个客运公司租了3辆60座和4辆45座的客车到该博物馆参观, 一天的租金共计6200元. ”
小萱:“如果我们七年级租用45座的客车a辆,那么还有15人没有座位;如果租用60座的客车可少租2辆,且正好坐满.”
根据以上对话,解答下列问题:
(1)、客运公司60座和45 座的客车每辆每天的租金分别是多少元?(2)、①参加此次活动的七年级师生共有 ▲ 人;②若同时租用两种或一种客车,要使每位师生都有座位,且每辆客车恰好坐满,应该怎样租用才合算?
五、解答题 (三) :本大题共2 小题,每小题12分,共24分.
-
23. 对x, y定义一种新的运算A, 规定: (其中ab≠0) .(1)、 若已知a=-2, b=1, 则A(4, 3) =;(2)、 已知A(1, 1)=5, A(-1, 2)=1, 求a, b的值;(3)、在(2)问的基础上,若关于正数p的不等式组 恰好有2个整数解,求m的取值范围.24. 【问题提出】小颖同学在学习中自主探究以下问题,请你解答她提出的问题:
 (1)、 如图1 所示, 已知AB∥CD, 点E为AB, CD之间一点, 连接BE, DE, 得到∠BED, 若∠B=20°, ∠D=30°, 则∠BED的度数为;(2)、【类比迁移】如图2所示, 已知AB∥CD,点E为AB, CD之间一点,∠ABE和∠CDE的平分线相交于点 F, 若∠E=α, 请用含α的式子表示∠F;(3)、【变式挑战】小颖结合角平分线的知识将问题进行深入探究,如图3 所示,已知AB∥CD, 点E的位置移到AB上方,点F在EB延长线上, ∠ABF与. 的平分线相交于点 G,请猜想∠G与∠E之间的数量关系,并说明理由.
(1)、 如图1 所示, 已知AB∥CD, 点E为AB, CD之间一点, 连接BE, DE, 得到∠BED, 若∠B=20°, ∠D=30°, 则∠BED的度数为;(2)、【类比迁移】如图2所示, 已知AB∥CD,点E为AB, CD之间一点,∠ABE和∠CDE的平分线相交于点 F, 若∠E=α, 请用含α的式子表示∠F;(3)、【变式挑战】小颖结合角平分线的知识将问题进行深入探究,如图3 所示,已知AB∥CD, 点E的位置移到AB上方,点F在EB延长线上, ∠ABF与. 的平分线相交于点 G,请猜想∠G与∠E之间的数量关系,并说明理由.