湘教版数学八年级上册《第2章 三角形》单元提升测试卷
试卷更新日期:2024-08-08 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,62. 将一副三角尺按如图所示的方式叠放,则的度数为( )
 A、 B、 C、 D、3. 用直角三角板作△ABC的高,下列作法正确的是( )A、
A、 B、 C、 D、3. 用直角三角板作△ABC的高,下列作法正确的是( )A、 B、
B、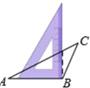 C、
C、 D、
D、 4. 如图,在中,是高,平分 , , , 则的度数是( )
4. 如图,在中,是高,平分 , , , 则的度数是( ) A、 B、 C、 D、5. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2 , 则S阴影等于( )
A、 B、 C、 D、5. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2 , 则S阴影等于( ) A、2cm2 B、1cm2 C、 cm2 D、 cm26. 如图,在中, , 将绕点逆时针旋转后得到 , 此时点恰好落在BD边上.若 , 则( )
A、2cm2 B、1cm2 C、 cm2 D、 cm26. 如图,在中, , 将绕点逆时针旋转后得到 , 此时点恰好落在BD边上.若 , 则( ) A、 B、 C、 D、7. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD,下列结论不一定正确的是( )
A、 B、 C、 D、7. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD,下列结论不一定正确的是( ) A、AD∥BC B、∠DAC=∠E C、BC⊥DE D、AD+BC=AE8. 如图,在中, , , 分别以点 , 点为圆心,大于的长为半径作弧,两弧交于点 , , 过点 , 作直线交于点 , 连结 , 则的周长为( )
A、AD∥BC B、∠DAC=∠E C、BC⊥DE D、AD+BC=AE8. 如图,在中, , , 分别以点 , 点为圆心,大于的长为半径作弧,两弧交于点 , , 过点 , 作直线交于点 , 连结 , 则的周长为( ) A、7 B、8 C、10 D、129. 用直尺和圆规作一个角等于已知角的作图痕迹如图所示,可得△ODC≌O'D'C' , 进一步得到∠O'=∠O . 上述作图中判定全等三角形的依据是( )
A、7 B、8 C、10 D、129. 用直尺和圆规作一个角等于已知角的作图痕迹如图所示,可得△ODC≌O'D'C' , 进一步得到∠O'=∠O . 上述作图中判定全等三角形的依据是( ) A、SSS B、SAS C、ASA D、AAS10. 如图,在和中,B,E,C,F在同一条直线上.下面给出5个论断:① , ② , ③ , ④ , ⑤ . 选其中3个作为条件,不能判定的是( ).
A、SSS B、SAS C、ASA D、AAS10. 如图,在和中,B,E,C,F在同一条直线上.下面给出5个论断:① , ② , ③ , ④ , ⑤ . 选其中3个作为条件,不能判定的是( ). A、①②③ B、②③④ C、③④⑤ D、①②④
A、①②③ B、②③④ C、③④⑤ D、①②④二、填空题(每题3分,共18分)
-
11. 如图,在△ABC中,AB=AC , ∠A=40°,按如下步骤作图:①以点B为圆心,适当长为半径画弧,分别交BA , BC于点D , E;②分别以点D , E为圆心,大于DE长为半径画弧,两弧在∠ABC的内部相交于点F , 作射线BF交AC于点G . 则∠ABG的大小为度.
 12. 如图,△ABC中,D是AB上一点,CF∥AB , D、E、F三点共线,请添加一个条件 , 使得AE=CE . (只添一种情况即可)
12. 如图,△ABC中,D是AB上一点,CF∥AB , D、E、F三点共线,请添加一个条件 , 使得AE=CE . (只添一种情况即可) 13. 一副三角板如图1摆放,把三角板绕公共顶点O顺时针旋转至图2,即时,的大小为 .
13. 一副三角板如图1摆放,把三角板绕公共顶点O顺时针旋转至图2,即时,的大小为 . 14. 如图,在中,是中线的中点.若的面积是1,则的面积是.
14. 如图,在中,是中线的中点.若的面积是1,则的面积是. 15. 等腰三角形一腰上的高与另一腰的夹角为52°,则该三角形的底角的度数为.16. 如图,在△ABC中,∠C=27°,点D在AC的垂直平分线上,将△ABD沿AD翻折后,使点B落在点B1处,线段B1D与AC相交于点E , 则∠CED= .
15. 等腰三角形一腰上的高与另一腰的夹角为52°,则该三角形的底角的度数为.16. 如图,在△ABC中,∠C=27°,点D在AC的垂直平分线上,将△ABD沿AD翻折后,使点B落在点B1处,线段B1D与AC相交于点E , 则∠CED= .
三、解答题(共8题,共72分)
-
17. 如图,△ABC中,AB=AC,点E,D,F分别在三边上,且BE=CD,CF=BD.
 (1)、求证:△BDE≌△CFD;(2)、若∠EDF=50°,求∠A的度数.18. 将两把大小相同的含30°角的三角尺(∠BAC=∠B'A'C=30°)按图①所示的方式放置,固定三角尺A'B'C,然后将三角尺ABC 绕直角顶点C 按顺时针方向旋转(旋转角小于 90°)至图②所示的位置,AB 与A'C相交于点E,AC 与A'B'相交于点F,AB与A'B'相交于点O.
(1)、求证:△BDE≌△CFD;(2)、若∠EDF=50°,求∠A的度数.18. 将两把大小相同的含30°角的三角尺(∠BAC=∠B'A'C=30°)按图①所示的方式放置,固定三角尺A'B'C,然后将三角尺ABC 绕直角顶点C 按顺时针方向旋转(旋转角小于 90°)至图②所示的位置,AB 与A'C相交于点E,AC 与A'B'相交于点F,AB与A'B'相交于点O. (1)、求证:△BCE≌△B'CF.(2)、当旋转角等于30°时,AB 与A'B'垂直吗? 请说明理由.19. 已知,如图,点、、、在同一直线上, , , .
(1)、求证:△BCE≌△B'CF.(2)、当旋转角等于30°时,AB 与A'B'垂直吗? 请说明理由.19. 已知,如图,点、、、在同一直线上, , , . (1)、求证:≌;(2)、当 , 时,求的度数.20. 综合与实践
(1)、求证:≌;(2)、当 , 时,求的度数.20. 综合与实践主题:研究旋转的奥妙.
素材:一张等边三角形硬纸板和一根木棍.
步骤:如图,将一根木棍放在等边三角形硬纸板上,木棍一端与等边三角形的顶点重合,点在上(不与点重合),将木棍绕点顺时针方向旋转 , 得到线段 , 点的对应点为 , 连接 .

猜想与证明:
(1)、直接写出线段与线段的数量关系.(2)、证明(1)中你发现的结论.21. (1)、问题发现:如图①,把一块三角板(AB=BC , ∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,发现与∠DAB始终相等的角是 , 与线段AD相等的线段是 .(2)、拓展探究:如图②,在△ABC中,点D在边BC上,并且DA=DE , ∠B=∠ADE=∠C . 求证:△ADB≌△DEC .(3)、能力提升:如图③,在等边△DEF中,A,C分别为DE、DF边上的点,AE=4,连接AC , 以AC为边在△DEF内作等边△ABC , 连接BF , 当∠CFB=30°时,请求出CD的长度.22. 请回忆华师版八年级上册数学教材第94页的部分内容,该内容阐述了垂直平分线的性质定理:线段垂直平分线上的点到线段两端钓距离相等;并给出了证明的方法。
(1)、问题发现:如图①,把一块三角板(AB=BC , ∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,发现与∠DAB始终相等的角是 , 与线段AD相等的线段是 .(2)、拓展探究:如图②,在△ABC中,点D在边BC上,并且DA=DE , ∠B=∠ADE=∠C . 求证:△ADB≌△DEC .(3)、能力提升:如图③,在等边△DEF中,A,C分别为DE、DF边上的点,AE=4,连接AC , 以AC为边在△DEF内作等边△ABC , 连接BF , 当∠CFB=30°时,请求出CD的长度.22. 请回忆华师版八年级上册数学教材第94页的部分内容,该内容阐述了垂直平分线的性质定理:线段垂直平分线上的点到线段两端钓距离相等;并给出了证明的方法。 (1)、定理证明:根据教材的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.(2)、定理应用:如图②,在△ABC中,直线m、n分别是边BC、AC的垂直平分线,直线m、n交于点O , 过点O作OH⊥AB于点H . 求证:AH=BH .(3)、如图③,在△ABC中,AB=BC , 边AB的垂直平分线交AC于点D , 边BC的垂直平分线交AC于点E . 若∠ABC=120°,AC=9,求DE的值是多少?23.
(1)、定理证明:根据教材的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.(2)、定理应用:如图②,在△ABC中,直线m、n分别是边BC、AC的垂直平分线,直线m、n交于点O , 过点O作OH⊥AB于点H . 求证:AH=BH .(3)、如图③,在△ABC中,AB=BC , 边AB的垂直平分线交AC于点D , 边BC的垂直平分线交AC于点E . 若∠ABC=120°,AC=9,求DE的值是多少?23. (1)、如图①,在中,的平分线与的平分线交于点O,求证:(2)、如图②,在中, E是边BC延长线上一点,的平分线与的平分线交于点O,求证:;(3)、如图③,在中,D是边延长线上一点,E是边延长线上一点,的平分线与的平分线交于点O. 试探求∠A与的数量关系并证明你的结论;24.
(1)、如图①,在中,的平分线与的平分线交于点O,求证:(2)、如图②,在中, E是边BC延长线上一点,的平分线与的平分线交于点O,求证:;(3)、如图③,在中,D是边延长线上一点,E是边延长线上一点,的平分线与的平分线交于点O. 试探求∠A与的数量关系并证明你的结论;24.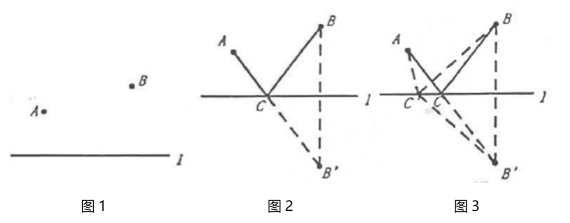
提出问题:早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者——海伦.一天,一位将军专程拜访他,请教一个百思不得其解的问题:如图1,将军每天从军营出发,先到河边饮马,然后再去军营开会,怎样走才能使路程最短?据说海伦略加思索就解决了它.这个问题被称为“将军饮马”的问题.你知道海伦是怎样解决这个问题的吗?
(1)、研究方法:第一步作其中一定点的对称点,第二步连接对称点和另一定点,第三步找与河(对称轴)的交点.如图2,此时最短,由轴对称的性质可得 , 所以最短.如图3,在直线上任取点 , 的理由是: .(2)、如图4,在等边 , , , 是的中点,是上的一点,则的最小值是;(请直接写出答案)(3)、如图5,在平面直角坐标系中,已知点 , 点 , 点在轴上运动,当的值最小时,点的坐标是;(请直接写出答案)(4)、如图6,于点 , 于点 , 且 , , 当点在直线上运动时,的最小值是 . (请直接写出答案)