湘教版数学八年级上册《第2章 三角形》单元同步测试卷
试卷更新日期:2024-08-08 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 以下列各组线段为边,能组成三角形的是( )A、2cm、10cm、13cm B、3cm、7cm、4cm C、4cm、4cm、4cm D、5cm、14cm、6cm2. 如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
 A、59° B、60° C、56° D、22°3. 如图,下面是三位同学的折纸示意图,则AD依次是的( )
A、59° B、60° C、56° D、22°3. 如图,下面是三位同学的折纸示意图,则AD依次是的( ) A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、中线、高线 D、角平分线、高线、中线4. 已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为( )
A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、中线、高线 D、角平分线、高线、中线4. 已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为( )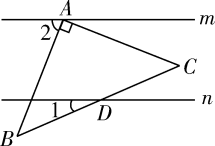 A、60° B、65° C、70° D、75°5. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且6. 如图,直线 .以直线 上的点A为圆心、适当长为半径画弧,分别交直线 于点B、C,连结 .若 ,则 的度数为( )
A、60° B、65° C、70° D、75°5. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且6. 如图,直线 .以直线 上的点A为圆心、适当长为半径画弧,分别交直线 于点B、C,连结 .若 ,则 的度数为( ) A、 B、 C、 D、7. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A、 B、 C、 D、7. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( ) A、50° B、70° C、75° D、80°8. 下面是“作一个角使其等于”的尺规作图方法.
A、50° B、70° C、75° D、80°8. 下面是“作一个角使其等于”的尺规作图方法.(1)如图,以点O为圆心,任意长为半径画弧,分别交 , 于点C , D;
(2)作射线 , 以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,两弧交于点;
(3)过点作射线 , 则.

上述方法通过判定得到 , 其中判定的依据是( )
A、三边分别相等的两个三角形全等 B、两边及其夹角分别相等的两个三角形全等 C、两角及其夹边分别相等的两个三角形全等 D、两角分别相等且其中一组等角的对边相等的两个三角形全等9. 如图,已知 , 添加选项( )仍不能证明 . A、 B、 C、 D、10. 如图,Rt中, , 要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )A、
A、 B、 C、 D、10. 如图,Rt中, , 要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )A、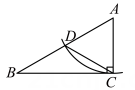 B、
B、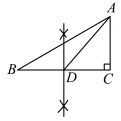 C、
C、 D、
D、
二、填空题(每题3分,共18分)
-
11. 如图,在中, , , 点在上且 , 连结 , 则.
 12. 如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为 cm.
12. 如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为 cm. 13. 如图,已知方格纸中鱼4个相同的正方形,则 .
13. 如图,已知方格纸中鱼4个相同的正方形,则 . 14. 如图,在中, , , 观察图中尺规作图的痕迹,则的度数为 .
14. 如图,在中, , , 观察图中尺规作图的痕迹,则的度数为 .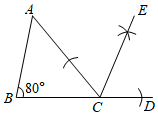 15. 如图,等腰三角形ABC的底边BC长为5,面积是20,腰AC的垂直平分线EF分别交AC , AB边于E , F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 .
15. 如图,等腰三角形ABC的底边BC长为5,面积是20,腰AC的垂直平分线EF分别交AC , AB边于E , F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 . 16. 如图,在中,的垂直平分线交于M , 的垂直平分线交于N , 连接、 , 若 , 则 .
16. 如图,在中,的垂直平分线交于M , 的垂直平分线交于N , 连接、 , 若 , 则 .
三、解答题(共9题,共72分)
-
17. 如图, , 点E在边上,与相交于点 . 若 , .
 (1)、求线段的长;(2)、求的度数.18. 如图,已知 , 分别是边上的高和中线,若 , , , .
(1)、求线段的长;(2)、求的度数.18. 如图,已知 , 分别是边上的高和中线,若 , , , . (1)、求的长度.(2)、求的面积.19. 如图,已知在与中,与交于点 , 且 , .
(1)、求的长度.(2)、求的面积.19. 如图,已知在与中,与交于点 , 且 , . (1)、求证:;(2)、当时,求的度数.20. 如图,已知 , 是的一个外角.
(1)、求证:;(2)、当时,求的度数.20. 如图,已知 , 是的一个外角. (1)、请用尺规作图法,作的平分线;(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 求证:.21. 如图,为任意三角形,以边、为边分别向外作等边三角形和等边三角形 , 连接、并且相交于点 .
(1)、请用尺规作图法,作的平分线;(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 求证:.21. 如图,为任意三角形,以边、为边分别向外作等边三角形和等边三角形 , 连接、并且相交于点 . (1)、求证:;(2)、 .22. 如图,点B、C、D在同一条直线上, , , , .
(1)、求证:;(2)、 .22. 如图,点B、C、D在同一条直线上, , , , . (1)、求证: .(2)、若 , 求的度数.23. 如图,点A,B,C在同一条直线上,点在BD上,且.
(1)、求证: .(2)、若 , 求的度数.23. 如图,点A,B,C在同一条直线上,点在BD上,且. (1)、求DE的长.(2)、判断直线AC与直线BD的位置关系,并说明理由.(3)、判断直线AD与直线CE的位置关系,并说明理由.24. (阅读理解)
(1)、求DE的长.(2)、判断直线AC与直线BD的位置关系,并说明理由.(3)、判断直线AD与直线CE的位置关系,并说明理由.24. (阅读理解)课外兴趣小组活动时,老师提出了如下问题:

如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)、由已知和作图能得到△ADC≌△EDB的理由是_____.A、SSS B、SAS C、AAS D、HL(2)、求得AD的取值范围是______.A、6<AD<8 B、6≤AD≤8 C、1<AD<7 D、1≤AD≤7(3)、解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.问题解决:
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
25. 已知,如图①,是等边三角形, , 是线段上的动点. (1)、问题解决:在图①中,若 , 根据给出的已知条件,直接写出一条未知线段的长度或一个角的大小;(2)、问题探究:如图②,在(1)的条件下,以线段为边在右侧作等边 , 连接 , 猜想与的数量关系并证明;(3)、拓展延伸:如图③,以线段为边在右侧作等边 , 在点从点向点的运动过程中,猜想点的运动路径是什么?当的值最小时,点运动路径的长度?(直接写出结果)
(1)、问题解决:在图①中,若 , 根据给出的已知条件,直接写出一条未知线段的长度或一个角的大小;(2)、问题探究:如图②,在(1)的条件下,以线段为边在右侧作等边 , 连接 , 猜想与的数量关系并证明;(3)、拓展延伸:如图③,以线段为边在右侧作等边 , 在点从点向点的运动过程中,猜想点的运动路径是什么?当的值最小时,点运动路径的长度?(直接写出结果)