浙教版数学八年级上册《第2章特殊三角形》单元同步测试卷

试卷更新日期：2024-08-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

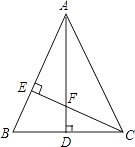
1. 已知一个等腰三角形的两边长分别为 $3$ 和 $5$ ，则它的周长为（）

A、 $11$ B、 $13$ C、 $11$ 或 $13$ D、 $12$ 或 $13$

查看试题解析
2. 如图，已知 $△ A B C$ 的面积为28， $A B = A C = 16$ ，点 $D$ 为 $B C$ 边上一点，过点 $D$ 分别作 $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ，若 $D F = 2 D E$ ，则 $D F$ 长为（）

A、 $\frac{7}{3}$ B、 $\frac{7}{6}$ C、 $\frac{16}{3}$ D、6

查看试题解析
3. 如图，在△ABC中，AB＝AC，D是BC的中点，下列结论不一定正确的是（）

A、∠B＝∠C B、AD＝2AB C、∠BAD＝∠CAD D、AD⊥BC

查看试题解析
4. 已知一个等腰三角形一内角的度数为80°，则这个等腰三角形顶角的度数为（）

A、20°或80° B、50°或80° C、80° D、100°

查看试题解析
5. 下列各组线段中，能构成直角三角形的是（）

A、2，3，4 B、3，4，6 C、5，12，13 D、4，6，7

查看试题解析
6. 《九章算术》是我国古代最重要的数学著作之一，它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈，末折抵地，去本四尺，问折者高几何？”翻译成数学问题是：如图所示， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C + A B = 10$ 尺， $B C = 4$ 尺，求AC的长.则AC的长为（）

A、4.2尺 B、4.3尺 C、4.4尺 D、4.5尺

查看试题解析
7. 如图，点P是∠BAC内一点，且点P到AB，AC的距离相等，则△PEA≌△PFA的理由是（）

A、HL B、AAS C、SSS D、ASA

查看试题解析
8. 如图所示，在△ABC中，∠BAC=60°，∠BAC的平分线AD与边BC的垂直平分线MD相交于点D，DE⊥AB交AB的延长线于点E，DF⊥AC于点F，现有下列结论：
①DE=DF；②DE+DF=AD；③DM平分∠EDF；④AB+AC=2AE.
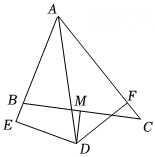
其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，点C在线段 $B D$ 上，且 $A B ⊥ B D$ ， $D E ⊥ B D$ ， $A B = C D$ ， $A C = C E$ ，下列说法错误的是（）

A、 $△ A B C ≌ △ C D E$ B、 $∠ A = ∠ E$ C、 $∠ A C E = 90 °$ D、 $B C = D E$

查看试题解析

二、填空题（每题3分，共18分）

10. 如图， $△ A B C$ 中， $A B = A C$ ， $B C = 5$ ， $S_{△ A B C} = 15$ ， $A D ⊥ B C$ 于点D， $E F$ 垂直平分 $A B$ ，交 $A C$ 于点F，在 $E F$ 上确定一点P，使 $P B + P D$ 最小，则这个最小值为．

查看试题解析
11. 如图所示的一块地，∠ADC=90°，CD=3，AD=4，AB=13，BC=12，求这块地的面积为.

查看试题解析
12. 若一个三角形的三边满足 $c^{2} - a^{2} = b^{2}$ ，则这个三角形是。

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $B C = 6$ ，以 $A B$ 、 $A C$ 为边作正方形，这两个正方形的面积和为．

查看试题解析
14. 如图，是一个三级台阶，它的每一级的长、宽，高分别为 $20 d m$ ， $3 d m$ 、 $2 d m$ ， $A$ 和 $B$ 是这个台阶两个相对的端点， $A$ 点有一只蚂蚁，想到 $B$ 点去吃可口的食物，则蚂蚁沿着台阶面爬到 $B$ 点的最短路程是 $d m$ 。

查看试题解析
15. 下列命题中逆命题是真命题的是.（写序号）
（ 1 ）直角三角形两条直角边的平方和等于斜边的平方；

（ 2 ）等腰三角形两腰上的高线相等；

（ 3 ）若三条线段 $a, b, c$ 是三角形的三边，则这三条线段满足 $a + b > c$ ；

（ 4 ）角的内部，到角两边距离相等的点在这个角的平分线上.

（ 5 ）全等三角形的面积相等.

查看试题解析

三、解答题（共8题，共72分）

16. 如图，在长度为1个单位长度的小正方形组成的正方形网格中， $△$ ABC的三个顶点A、B、C都在格点上．

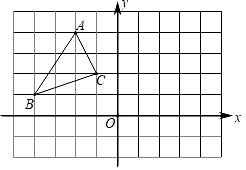
（ 1 ）在图中画出与 $△$ ABC关于直线y成轴对称的 $△$ A₁B₁C₁；

（ 2 ）求 $△$ ABC的面积；

（ 3 ）在x轴上找出一点P，使得PB+PC的值最小．（不需计算，在图上直接标记出点P的位置）

查看试题解析
17. 如图，已知AD，AE分别是Rt△ABC的高和中线，∠BAC=90°．

(1)、若AB=6cm，AC=8cm，BC=10cm，求AD的长；

(2)、若∠C＝30°，求∠DAE的度数．

查看试题解析
18. 如图1，在△ABC中，AB=AC，P为底边BC上一点，PE⊥AB，PF⊥AC，CH⊥AB，垂足分别为E，F，H．易证PE+PF=CH．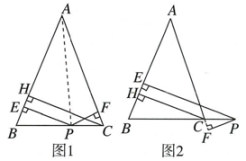
证明过程如下：
如图1，连结AP．
∵PE⊥AB，PF⊥AC，CH⊥AB，
∴S_△_ABP= $\frac{1}{2}$ AB·PE，S_△_ACP= $\frac{1}{2}$ AC·PF，S_△_AB_C= $\frac{1}{2}$ AB·CH．
又∵S_△_ABP+S_△_ACP=S_△_ABC ，
∴AB·PE+AC·PF=AB·CH．
∵AB=AC，
∴PE+PF=CH．
如图2，当P为BC延长线上的点时，其他条件不变，PE，PF，CH又有怎样的数量关系？请写出你的猜想，并加以证明．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B$ 的垂直平分线 $D M$ 交 $B C$ 于点 $D$ ，边 $A C$ 的垂直平分线 $E N$ 交 $B C$ 于点E．

(1)、已知 $△ A D E$ 的周长 $7 c m$ ，求 $B C$ 的长；

(2)、若 $∠ A B C = 30 °$ ， $∠ A C B = 40 °$ ，求 $∠ D A E$ 的度数．

查看试题解析
20. 如图所示，A城与C城的直线距离为60公里，B城与C城的直线距离为80公里，A城与B城的直线距离为100公里．

(1)、现需要在A ， B ， C三座城市所图成的三角形区域内建造一个加油站 $P$ ．使得这个加油站 $P$ 到三座城市A ， B ， C的距离相等，则加油站 $P$ 点一定是 $△ A B C$ 三条的交点；（请在以下选项中选出正确答案并将对应选项序号填写在横线上：①中线②高线③角平分线④垂直平分线）

(2)、判断 $△ A B C$ 形状，并说明理由．

查看试题解析
21. 如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：

(1)、△AEF≌△CEB；

(2)、AF=2CD．

查看试题解析
22. 如图，一架云梯AB的长25m，斜靠在一面墙上，梯子靠墙的一端A距地面距离AC为24m．

(1)、这个梯子底端B离墙的距离BC有多少米？

(2)、如果梯子的顶端下滑了4m，那么梯子的底部在水平方向也滑动了4 m吗？为什么？

查看试题解析

浙教版数学八年级上册《第2章 特殊三角形》单元同步测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

浙教版数学八年级上册《第2章特殊三角形》单元同步测试卷