北师大版数学九年级上册《第二章一元二次方程》单元提升测试卷

试卷更新日期：2024-08-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 若方程 $(a - 1) x^{2} + x = 1$ 是关于x的一元二次方程，则a的取值范围是（）

A、 $a \neq 1$ B、 $a \neq 0$ C、 $a \geq 0$ 且 $a \neq 1$ D、 $a > 1$

查看试题解析
2. 用配方法解方程 $2 x^{2} - x - 1 = 0$ 时．变形结果正确的是（）

A、 ${(x - \frac{1}{4})}^{2} = \frac{9}{16}$ B、 ${(x - \frac{1}{2})}^{2} = \frac{3}{4}$ C、 ${(x - \frac{1}{4})}^{2} = \frac{17}{16}$ D、 ${(x - \frac{1}{4})}^{2} = \frac{3}{4}$

查看试题解析
3. 关于 $x$ 的一元一次方程 $(m + 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是（）

A、 $m < 0$ 且 $m \neq - 1$ B、 $m ⩾ 0$ C、 $m ⩽ 0$ 且 $m \neq - 1$ D、 $m < 0$

查看试题解析
4. 对于任意4个实数a ， b ， c ， d定义一种新的运算 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，例如： $| \begin{array}{l} 4 & 2 \\ 1 & 6 \end{array} | = 4 \times 6 - 2 \times 1 = 22$ ，则关于x的方程 $| \begin{array}{l} x & 4 \\ 2 & x - k \end{array} | = 0$ 的根的情况为（）

A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
5. 若关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 4 m - 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $(x_{1} + 2) (x_{2} + 2) - 2 x_{1} x_{2} = 17$ ，则 $m =$ （）

A、2或6 B、2或8 C、2 D、6

查看试题解析
6. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 2022 = 0$ 的两个实数根，则代数式 $x_{1}^{3} - 2022 x_{1} + x_{2}^{2}$ 的值是（）

A、4045 B、4044 C、2022 D、1

查看试题解析
7. 如图，在一块长为36米，宽为25米的矩形空地上修建三条宽均为x米的笔直小道，其余部分（即图中阴影部分）改造为草坪进行绿化，若草坪的面积为840平方米，求x的值.根据题意，下列方程正确的是（）

A、 $36 \times 25 - 36 x - 25 x = 840$ B、 $36 x + 25 x = 840$ C、 $(36 - x) (25 - x) + x^{2} = 840$ D、 $(36 - x) (25 - x) = 840$

查看试题解析
8. 某班学生毕业时，每个同学都要给其他同学写一份留言纪念，全班同学共写了1980份留言，如果全班同学有x名学生，根据题意，下列方程正确的是（）

A、x（x﹣1）＝1980 B、x（x+1）＝1980 C、 $\frac{x （ x ﹣ 1 ）}{2} = 1980$ D、 $\frac{x （ x + 1 ）}{2} = 1980$

查看试题解析
9. 眉山市东坡区永丰村是“天府粮仓”示范区，该村的“智慧春耕”让生产更高效，提升了水稻亩产量，水稻亩产量从2021年的670千克增长到了2023年的780千克，该村水稻亩产量年平均增长率为 $x$ ，则可列方程为（）

A、 $670 \times (1 + 2 x) = 780$ B、 $670 \times {(1 + x)}^{2} = 780$ C、 $670 \times (1 + x^{2}) = 780$ D、 $670 \times (1 + x) = 780$

查看试题解析
10. 端午节又称端阳节，是中华民族重要的传统节日，我国各地都有吃粽子的习俗．某超市以10元每袋的
价格购进一批粽子，根据市场调查，售价定为每袋16元，每天可售出200袋；若售价每降低1元，则可多
售出80袋，问此种粽子售价降低多少元时，超市每天售出此种粽子的利润可达到1440元？若设每袋粽子
售价降低x元，则可列方程为（）

A、 $(16 - x - 10) (200 + 80 x) = 1440$ B、 $(16 - x) (200 + 80 x) = 1440$ C、 $(16 - x - 10) (200 + 80 x) = 1440$ D、 $(16 - x) (200 + 80) = 1440$

查看试题解析

二、填空题（每题3分，共18分）

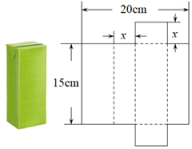
11. 若关于x的一元二次方程x²+2x﹣m=0有两个相等的实数根，则m的值为．

查看试题解析
12. 已知方程 $x^{2} + x - 2 = 0$ 的两根分别为 $x_{1}$ ， $x_{2}$ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为．

查看试题解析
13. 随着经济复苏，某公司近两年的总收入逐年递增.该公司2021年缴税40万元，2023年缴税48.4万元，该公司这两年缴税的年平均增长率是.

查看试题解析
14. 已知等腰三角形的一边长为9，另一边长为方程x²﹣8x+15=0的根，则该等腰三角形的周长为．

查看试题解析
15. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
16. 图①中有一首古算诗，根据诗中的描述可以计算出红莲所在位置的湖水深度，其示意图如图②，其中AB＝AB^' ， AB⊥B^'C于点C ， BC＝0.5尺，B^'C＝2尺．设AC的长度为x尺，可列方程为．

查看试题解析

三、解答题（共8题，共72分）

17. 用配方法解方程x²﹣4x﹣5＝0．

查看试题解析
18. 解方程：

(1)、 $x^{2} - 2 x - 35 = 0$ ；

(2)、 ${(x + 3)}^{2} = 2 x + 6$ .

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - p x + 1 = 0$ （p为常数）有两个不相等的实数根 $x_{1}$ 和 $x_{2}$ .

(1)、填空： $x_{1} + x_{2} =$ ， $x_{1} x_{2} =$ ；

(2)、求 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ， $x_{1} + \frac{1}{x_{1}}$ ；

(3)、已知 $x_{1}^{2} + x_{2}^{2} = 2 p + 1$ ，求p的值.

查看试题解析
20. 关于 $x$ 的一元二次方程 $x^{2} + 2 x + 3 - k = 0$ 有两个不相等的实数根．

(1)、求 $k$ 的取值范围；

(2)、若方程的两个根为 $α$ ， $β$ ，且 $k^{2} = α β + 3 k$ ，求 $k$ 的值．

查看试题解析
21. 已知关于 $x$ 的方程 $k^{2} x^{2} - 2 (k - 1) x + 1 = 0$ 有两个实数根 $x_{1}$ 、 $x_{2}$ .

(1)、求 $k$ 的取值范围.

(2)、若 $x_{1}$ 、 $x_{2}$ 满足等式 $| x_{1} + x_{2} | = 5 x_{1} x_{2} - 1$ ，求 $k$ 的值.

查看试题解析
22. 已知关于x的一元二次方程x²﹣（2m+1）x+m²+m＝0．

(1)、求证：无论m取何值时，方程都有两个不相等的实数根；

(2)、设该方程的两个实数根为x₁ ， x₂ ．
①求代数式； $x_{1}^{2} + x_{2}^{2} - 4 x_{1} x_{2}$ 的最大值；
②若方程的一个根是6，x₁和x₂是一个等腰三角形的两条边，求等腰三角形的周长．

查看试题解析
23. 阅读材料：
材料：关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根 $x_{1}, x_{2}$ 和系数 $a$ ， b，c有如下关系： $x_{1} + x_{2} = - \frac{b}{a}, x_{1} x_{2} = \frac{c}{a}$ ；
根据上述材料，结合你所学的知识，完成下列问题：

(1)、类比：一元二次方程 $2 x^{2} + 3 x - 1 = 0$ 的两个实数根为m，n，则 $m + n =$ ；mn=；

(2)、应用：已知一元一次方程 $2 x^{2} + 3 x - 1 = 0$ 的两个实数根为m，n，求 $m^{2} + n^{2}$ 的值；

(3)、提升：已知实数s，t满足 $2 s^{2} + 3 s - 1 = 0, 2 t^{2} + 3 t - 1 = 0$ 且 $s \neq t$ ，求 $\frac{1}{s} - \frac{1}{t}$ 的值.

查看试题解析
24. 某商场销售一批衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加利润，尽快减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件.

(1)、若每件衬衫降价5元，则商场平均每天可售出衬衫件，每天获得的利润为元。

(2)、若商场每天要获得利润1200元，请计算出每件衬衫应降价多少元？

(3)、商场每天要获得利润有可能达到1400元吗？若能，请求出此时每件衬衫的利润；若不能，请说明理由

查看试题解析

北师大版数学九年级上册《第二章 一元二次方程》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学九年级上册《第二章一元二次方程》单元提升测试卷