北师大版数学八年级上册《第二章实数》单元提升测试卷

试卷更新日期：2024-08-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在给出的一组数0，π， $\sqrt{5}$ ， 3.14， $\sqrt[3]{9}$ ， $\frac{22}{7}$ 中，无理数有（　　）

A、1个 B、2个 C、3个 D、5个

查看试题解析
2. 若 $m + 4$ 与 $m - 2$ 是同一个正数的两个平方根，则m的值为（　　）

A、3 B、 $- 3$ C、1 D、 $- 1$

查看试题解析
3. $\sqrt{16}$ 的平方根是（　　）

A、4 B、±4 C、±2 D、2

查看试题解析
4. 下列说法正确的是（）

A、无限小数都是无理数 B、 $- \frac{1}{125}$ 没有立方根 C、正数的两个平方根互为相反数 D、 $- (- 13)$ 没有平方根

查看试题解析
5. 甲、乙、丙三人对平方根和立方根进行了研究，以下是他们三人的结论：
甲：当 $a > 0$ 时， $\sqrt{a^{2}} = a$ 乙： $a < 0$ 时， $- \sqrt{a^{2}} = - a$ 丙：当 $a > 0$ 时， $\sqrt[3]{- a} = - \sqrt[3]{a}$ 则下列说法正确的是（）.

A、只有甲、乙正确 B、只有甲、丙正确 C、甲、乙、丙都正确 D、甲、乙、丙都不正确

查看试题解析
6. 若 $3 + \sqrt{5}$ 的小数部分是a， $3 - \sqrt{5}$ 的小数部分是b，则a+b的值为（）

A、0 B、1 C、-1 D、2

查看试题解析
7. 如图的数轴上，点 $A$ ， $C$ 对应的实数分别为1，3，线段 $A B ⊥ A C$ 于点 $A$ ，且 $A B$ 长为1个单位长度.若以点 $C$ 为圆心， $B C$ 长为半径的弧交数轴于0和1之间的点 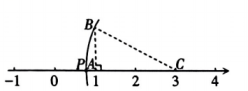$P$ ，则点 $P$ 表示的实数为（）

A、 $3 - \sqrt{5}$ B、 $\sqrt{5} - 2$ C、 $\sqrt{5} - 1$ D、 $3 - \sqrt{10}$

查看试题解析
8. 下列计算，正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{(- 2) \times (- 2)} = 2$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$

查看试题解析
9. 把 $m \sqrt{- \frac{1}{m}}$ 根号外的因式移到根号内，得（）

A、 $\sqrt{m}$ B、- $\sqrt{m}$ C、- $\sqrt{- m}$ D、 $\sqrt{- m}$

查看试题解析
10. 下列各式中，一定成立的是（）

A、 $\sqrt[]{{(a + b)}^{2}} = a + b$ B、 $\sqrt[]{{(a^{2} + 1)}^{2}} = a^{2} + 1$ C、 $\sqrt[]{a^{2} - 1} = \sqrt{a + 1} \cdot \sqrt{a - 1}$ D、 $\sqrt{\frac{a}{b}} = \frac{1}{b} \sqrt{a b}$

查看试题解析

二、填空题（每题3分，共18分）

11. 已知正数m的两个平方根是2a-1与2-a，则m的值为．

查看试题解析
12. 规定用符号 $[m]$ 表示一个实数 $m$ 的整数部分，例如 $[0.6] = 0$ ， $[3.14] = 3$ ，按此规定 $[\sqrt{10} + 2]$ 的值为．

查看试题解析
13. 点 $A$ 在数轴上表示的数是 $- \sqrt{15}$ ，点 $B$ 在数轴上表示的数为 $\sqrt{7}$ ，则A、B之间表示的整数点有个.

查看试题解析
14. 实数 $a$ 、 $b$ 在数轴上位置如图，化简： $| a + b | + \sqrt{{(a - b)}^{2}} =$ ；

查看试题解析
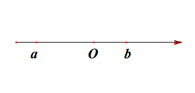15. 观察下列等式：
第1个等式： $a_{1} = \frac{1}{1 + \sqrt{2}}$ $=$ = $\sqrt{2}$ $- 1$ ，
第 $2$ 个等式： $a_{2} = \frac{1}{\sqrt{2} + \sqrt{3}}$ = $=$ $\sqrt{3} - \sqrt{2}$ ，
第 $3$ 个等式： $a_{3} = \frac{1}{\sqrt{3} + 2}$ $= 2 -$ $\sqrt{3}$ ，
第 $4$ 个等式： $a_{4} = \frac{1}{2 + \sqrt{5}}$ = $=$ $\sqrt{5}$ $- 2$ ，
…
按上述规律，计算 $a_{1} + a_{2} + a_{3} ⋯ + a_{n} =$ ．

查看试题解析
16. 已知x，y为实数，且 $y = \sqrt{x - 2024} - \sqrt{2024 - x} + 2000$ ，则 $\sqrt{x - y}$ =.

查看试题解析

三、解答题（共9题，共72分）

17. 计算： $\sqrt{48} \div \sqrt{3} + \sqrt{\frac{1}{2}} \times \sqrt{12} - \sqrt{24}$ .

查看试题解析
18. 计算： $\sqrt{75} \div \sqrt{3} + \sqrt{\frac{1}{2}} \times \sqrt{18} - {(\sqrt{6} + \sqrt{2})}^{2}$

查看试题解析
19. 计算： $7 a \sqrt{8 a} - 4 a^{2} \sqrt{\frac{1}{8 a}} + 7 a \sqrt{2 a}$ ．

查看试题解析
20. 计算： $\frac{3}{5} \sqrt{a b^{2}} \cdot (- \frac{5}{6} \sqrt{a^{3} b}) \div \frac{4}{15} \sqrt{\frac{b^{2}}{a}}$ ．

查看试题解析
21. 已知 $a$ ， $b$ ， $m$ 都是实数，若 $a + b = 2$ ，则称 $a$ 与 $b$ 是关于 $l$ 的“平衡数”．

(1)、 $4$ 与是关于 $l$ 的“平衡数”， $3 - \sqrt{2}$ 与是关于 $l$ 的“平衡数”；

(2)、若 $（ m + \sqrt{3} ）（ 1 - \sqrt{3} ） = - 2$ ，判断 $m + \sqrt{3}$ 与 $2 - \sqrt{3}$ 是否是关于 $l$ 的“平衡数”，并说明理由．

查看试题解析
22. 我们在学习二次根式时，了解了分母有理化及其应用．其实，还有一个类似的方法叫做“分子有理化”，即分母和分子都乘以分子的有理化因式，从而消除分子中的根式．
比如： $\sqrt{7} - \sqrt{6} = \frac{(\sqrt{7} - \sqrt{6}) (\sqrt{7} + \sqrt{6})}{\sqrt{7} + \sqrt{6}}$ ＝ $\frac{1}{\sqrt{7} + \sqrt{6}}$ ．

分子有理化可以用来比较某些二次根式的大小，也可以用来处理一些二次根式的最值问题．例如：比较： $\sqrt{7} - \sqrt{6}$ 和 $\sqrt{6} - \sqrt{5}$ 的大小可以先将它们分子有理化如下： $\sqrt{7} - \sqrt{6} = \frac{1}{\sqrt{7} + \sqrt{6}}$ ， $\sqrt{6} - \sqrt{5} = \frac{1}{\sqrt{6} + \sqrt{5}}$ ．

因为 $\sqrt{7} + \sqrt{6} > \sqrt{6} + \sqrt{5}$ ，所以， $\sqrt{7} - \sqrt{6} < \sqrt{6} - \sqrt{5}$ ．

再例如，求y＝ $\sqrt{x + 2} - \sqrt{x - 2}$ 的最大值、做法如下：

解：由x＋2≥0，x﹣2≥0可知x≥2，而y＝ $\sqrt{x + 2} - \sqrt{x - 2}$ ＝ $\frac{4}{\sqrt{x + 2} + \sqrt{x - 2}}$ ．当x＝2时，分母 $\sqrt{x + 2} + \sqrt{x - 2}$ 有最小值2.所以y的最大值是2

利用上面的方法，完成下面问题：

(1)、比较 $\sqrt{19}$ ﹣ $\sqrt{18}$ 和 $\sqrt{18}$ ﹣ $\sqrt{17}$ 的大小；

(2)、求y＝ $\sqrt{x + 1}$ ﹣ $\sqrt{x - 1}$ ＋2的最大值．

查看试题解析
23. 我们知道 $\sqrt{2}$ 是无理数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如： $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，所以 $\sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ ．
请根据以上信息，回答下列问题：

(1)、 $\sqrt{34}$ 整数部分是，小数部分是；

(2)、如果 $\sqrt{11}$ 的整数部分为 $a ， \sqrt{17}$ 的整数部分为 $b$ ，求 $12 a + 7 b$ 的立方根；

(3)、已知 $9 - \sqrt{7} = x - y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，求 $x + y$ 的值．

查看试题解析
24. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $3 a + b - 9$ 的立方根是 $2$ ， $c$ 是 $\sqrt{5}$ 的整数部分．

(1)、求 $a$ 和 $b$ 的值；

(2)、求 $a + 2 b - c + 2$ 的算术平方根．

查看试题解析
25. [阅读材料]在解决数学问题时，我们要仔细阅读题干。找出有用信息，然后利用这些信息解决问题。有些题目信息比较明显。我们把这样的信息称为显性条件s而有些信息不太明显，需要结合图形、特殊式子成立的条件、实际问题等发现总合你总作为条件。我们把这样的条件称为隐含条件。做题时。我们要注意发现题目中的隐含条件。

(1)、[感知探索]补全下面两个问题的解答过程：
已知a≤1，化简 $\sqrt{(a - 1)^{2}} - (\sqrt{2 - a})^{2}$
解：原式=|a-1|-（2-a）．
∵a≤1．显性条件
请进一步完成 $\sqrt{(a - 1)^{2}} - (\sqrt{2 - a})^{2}$ 的化简、

(2)、三角形的三边长分别为2、5、m．化简 $\sqrt{(m - 3)^{2}} + \sqrt{m^{2} - 14 m + 49}$ ．
解：三角形的三边长分别为2、5、m．
∴m的取值范围是隐含条件
化简 $\sqrt{(m - 3)^{2}} + \sqrt{m^{2} - 14 m + 49}$ ．

(3)、[拓展应用]解方程： $(\sqrt{x - 2})^{2} + \sqrt{(3 - 2 x)^{2}} = 1$ ．

查看试题解析

北师大版数学八年级上册《第二章 实数》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

北师大版数学八年级上册《第二章实数》单元提升测试卷