北师大版（2024）数学七年级上册《 第一章 丰富的图形世界》单元提升测试卷
试卷更新日期：2024-08-06 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 下列常见的几何体中，主视图和左视图不同的是（ ）A、
B、
C、
D、
2. 用5个大小相同的小正方体搭一个几何体，其主视图、左视图如图2，现将其中4个小正方体按图1方式摆放，则最后一个小正方体应放在（ ）
A、①号位置 B、②号位置 C、③号位置 D、④号位置3. 如图是由5个相同的小立方块搭成的几何体，这个几何体的俯视图是（ ）
A、
B、
C、
D、
4. 由5个形状、大小完全相同的小正方体组合而成的几何体，其主视图和左视图如图所示，则搭建该几何体的方式有（ ）
A、1种 B、2种 C、3种 D、4种5. 将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（ ）
A、
B、
C、
D、
6. 由5个棱长为1的小正方体组成的几何体如图放置，一面着地，两面靠墙．如果要将露出来的部分涂色，则涂色部分的面积为（ ）
A、10 B、11 C、12 D、137. 有一块正方体木块，它的六个面上分别标上数字1~6，下图是这个正方体木块从不同面所看到的数字情况，请问1对面的数字是（ ）
A、3 B、4 C、6 D、28. 如图是的正方形网格，选择一空白小正方形，能与阴影部分组成正方体展开图的方法有（ ）
A、1种 B、2种 C、3种 D、4种9. 走马灯，又称仙音烛，据史料记载，走马灯的历史起源于隋唐时期，盛行于宋代，是中国特色工艺品，常见于除夕、元宵、中秋等节日，在一次综合实践活动中，一同学用如图所示的纸片，沿折痕折合成一个棱锥形的“走马灯”，正方形做底，侧面有一个三角形面上写了“祥”字，当灯旋转时，正好看到“吉祥如意”的字样.则在A、B、C处依次写上的字可以是( )
A、吉如意 B、意吉如 C、吉意如 D、意如吉10. 如图所示的几何体由六块相同的小正方体搭成，若移走一块小正方体几何体的左视图发生了改变，则移走的小正方体是（ ）
A、① B、② C、③ D、④二、填空题（每题3分，共18分）
-
11. 用若干个相同的小正方体搭一个几何体，该几何体的主视图、俯视图如图所示.若小正方体的棱长为1，则搭成的几何体的表面积是.
12. 已知一个直棱柱共有15条棱，它的底面边长都是5cm，侧棱长都是4cm，则这个棱柱的所有侧面的面积之和是 ．13. 表的指针旋转时，会形成一个圆面，笔在纸上移动时，能画出线．一般地，点动成线， ， ．14. 从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为 ．
15. 如图所示，用经过A ， B ， C三点的平面截去正方体的一角，变成一个新的多面体，若这个多面体的面数为m ， 棱数为n ， 则.
16. 如图是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图，若这个几何体最多由m个小正方体组成，最少由n个小正方体组成，则2m+3n＝ ．
三、解答题（共8题，共72分）
-
17. 已知长方形的长为4cm、宽为3cm ， 将其绕它的一边所在的直线旋转一周，得到一个几何体，
(1)、求此几何体的表面积．（结果保留π）(2)、求此几何体的体积；（结果保留π）18. 【问题情境】小明所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔．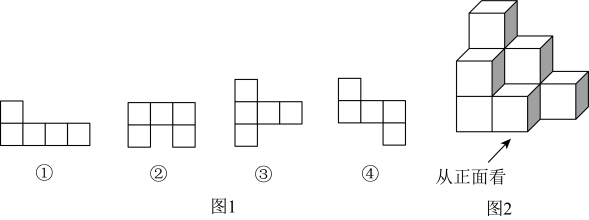
【操作探究】
(1)、图1中的第个图形经过折叠不能围成无盖正方体纸盒（填序号）．(2)、小圣所在的综合实践小组把折叠成9个棱长都为的无盖正方体纸盒摆成如图2所示的几何体．①请计算出这个几何体的表面积；
②要保持从上面看到的平面图形不变，最多可以拿走小正方体的个数是 ▲ ．
19. 如图所示，把一个底面半径是5cm、高是8cm的圆柱放在水平桌面上.
(1)、若用一个平面沿水平方向去截这个圆柱，所得的截面是；(2)、若用一个平面沿竖直方向去截这个圆柱，所得的截面是；(3)、若用一个平面去截这个圆柱，使截得的截面是长方形，且长方形的截面面积最大，请写出截法，并求出此时截面的面积.20. 如图，这是一个缺少一个面的正方体纸盒的表面展开图.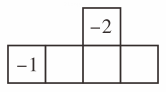
(1)、在图中补上缺少的这个面，使得折叠后能围成一个正方体.(2)、请把 ， ， ， 分别填入没有填数的三个正方形和（1）中所补的一个正方形中，使得折叠成正方体后，相对的面上的两个数的和都等于.21. 在一次数学综合实践活动中，需要制作如图所示的零件（长方体和圆锥的组合体），为此方方同学画出了该零件的三视图．
(1)、请问方方所画的三个视图是否有错？如有错，请将错的视图改正．(2)、根据图中尺寸，求出其体积．（注：长方体的底面为正方形，单位：cm ， 结果保留一位小数）22. 如图，观察下列几何体并回答问题．
(1)、请观察所给几何体的面、棱、顶点的数量并归纳出棱柱有个面，条棱，个顶点；棱锥有个面，条棱，个顶点；(2)、所有像三棱柱、四棱柱、六棱柱、三棱锥等这样由四个或四个以上多边形所围成的立体图形叫做多面体，经过前人们归纳总结发现，多面体的面数 ， 顶点个数以及棱的条数存在着一定的关系，请根据（1）总结出这个关系为 ．23.如图①、②、③、④四个图形都是平面图形，观察图②和表中对应数值，探究计数的方法并解答下面的问题．
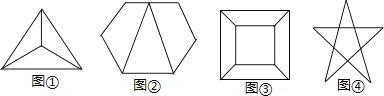
（1）数一数每个图各有多少顶点、多少条边、这些边围成多少区域，将结果填入下表：
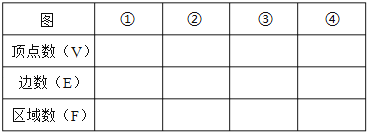
（2）根据表中的数值，写出平面图的顶点数、边数、区域数之间的关系；
（3）如果一个平面图形有20个顶点和11个区域，求这个平面图形的边数．
24. 综合实践问题情景：某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究：
(1)、若准备制作一个无盖的正方体形纸盒，如图1，下面的哪个图形经过折叠能围成无盖正方体形纸盒？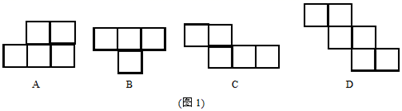
(2)、如图2是小明的设计图，把它折成无盖正方体形纸盒后与“保”字相对的是哪个字？
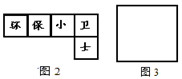(3)、如图3，有一张边长为20cm的正方形废弃宣传单，小华准备将其四角各剪去一个小正方形，折成无盖长方体形纸盒.①请你在图3中画出示意图，用实线表示剪切线，虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形，用含x的代数式表示这个纸盒的高以及底面积，当小正方形边长为4cm时，求纸盒的容积.