浙教版数学八年级上册《第1章 三角形的初步知识》单元提升测试卷
试卷更新日期:2024-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在中, , AE平分 , 若 , , 则的度数是( )
 A、10° B、12° C、13° D、15°2. 如图,点P是△ABC的AB边上一动点,当S△APC=S△BPC时,则CP是△ABC的( )
A、10° B、12° C、13° D、15°2. 如图,点P是△ABC的AB边上一动点,当S△APC=S△BPC时,则CP是△ABC的( ) A、高 B、中线 C、角平分线 D、中位线3. 小红同学在一次作业中完成了以下作图步骤:
A、高 B、中线 C、角平分线 D、中位线3. 小红同学在一次作业中完成了以下作图步骤:①在和上分别截取 , , 使;
②分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;
③作射线 , 连接 , , 如图所示.

根据以上作图,一定可以推得的结论是
A、且 B、且 C、且 D、且4.如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
 A、0 B、1 C、2 D、35. 如图 , 在矩形 中, , 延长 至点 , 使 , 连结 , 动点 从点 出发, 以每秒 2 个单位的速度沿 向终点 运动. 设点 的运动时间为 , 要使 和 全等,则 的值为( )
A、0 B、1 C、2 D、35. 如图 , 在矩形 中, , 延长 至点 , 使 , 连结 , 动点 从点 出发, 以每秒 2 个单位的速度沿 向终点 运动. 设点 的运动时间为 , 要使 和 全等,则 的值为( ) A、1 B、1 或 3 C、1 或 7 D、3 或 76. 如上图,点B、F、C、E都在一条直线上, , 添加下列一个条件后,仍无法判断的是( )
A、1 B、1 或 3 C、1 或 7 D、3 或 76. 如上图,点B、F、C、E都在一条直线上, , 添加下列一个条件后,仍无法判断的是( ) A、 B、 C、 D、7. 如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE , AE交BC于点D , CD=5,P为AB上一动点,则PD的最小值为( )
A、 B、 C、 D、7. 如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE , AE交BC于点D , CD=5,P为AB上一动点,则PD的最小值为( ) A、2 B、3 C、4 D、58. 为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.
A、2 B、3 C、4 D、58. 为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.甲:如图1,先过点B作的垂线 , 再在射线上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E,则测出的长即为A,B间的距离;
乙:如图2,先确定直线 , 过点B作射线 , 在射线上找可直接到达点A的点D,连接 , 作 , 交直线于点C,则测出的长即为A,B间的距离,则下列判断正确的是( )
 A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行9. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )
A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行9. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )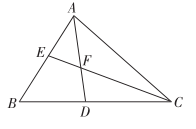
①;②;③若 , 则;④ .
A、1个 B、2个 C、3个 D、4个10. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB , 其中正确的有( )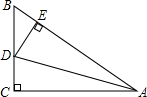 A、2个 B、3个 C、4个 D、1个
A、2个 B、3个 C、4个 D、1个二、填空题(每题3分,共18分)
-
11. 如图,在 中, 厘米, , 厘米,点 为 的中点.如果点 在线段 上以4厘米/秒的速度由 点向 点运动,同时,点 在线段 上由 点向 点运动.当点 的运动速度为厘米/秒时,能够在某一时刻使 与 全等.
 12. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是.
12. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是. 13. 如图,在中, , , , 则的度数是
13. 如图,在中, , , , 则的度数是 14. 如图, , , , 此时点恰好在线段上,则的度数为 .
14. 如图, , , , 此时点恰好在线段上,则的度数为 . 15. 如图,在中, , 平分 , 若 , , 则 .
15. 如图,在中, , 平分 , 若 , , 则 . 16. 如图①是某种型号拉杆箱的实物图,如图②是它的几何示意图,行李箱的侧面可看成一个矩形,点F,C,D在同一直线上,为了拉箱时的舒适度,现将调整为 , 保持不变(恒等为),则图中应为 .
16. 如图①是某种型号拉杆箱的实物图,如图②是它的几何示意图,行李箱的侧面可看成一个矩形,点F,C,D在同一直线上,为了拉箱时的舒适度,现将调整为 , 保持不变(恒等为),则图中应为 .
三、解答题(共8题,共72分)
-
17. 如图,中,点D在边上, , 的平分线交于点E , 过点E作 , 垂足为 , 且 , 连接 .
 (1)、求证:平分;(2)、若 , 求的面积.18. 已知:AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,
(1)、求证:平分;(2)、若 , 求的面积.18. 已知:AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F, (1)、如图1,求证:BE=CD.(2)、如图2,连接AF,在不添加任何辅助线的情况下,请直接写出图2中所有的全等三角形.19. 如图①,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图②,伞圈D沿着伞柄滑动时,伞柄始终平分同一平面内两条伞骨所成的 , 伞骨 , 的B , C点固定不动,且到点A的距离 .
(1)、如图1,求证:BE=CD.(2)、如图2,连接AF,在不添加任何辅助线的情况下,请直接写出图2中所有的全等三角形.19. 如图①,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图②,伞圈D沿着伞柄滑动时,伞柄始终平分同一平面内两条伞骨所成的 , 伞骨 , 的B , C点固定不动,且到点A的距离 . (1)、当D点在伞柄上滑动时,处于同一平面的两条伞骨和相等吗?请说明理由.(2)、如图③,当油纸伞撑开时,伞的边缘M , N与点D在同一直线上,若 , , 求的度数.20. 两个大小不同的等腰直角三角板如图所示放置,右图是由它抽象出的几何图形,B , C , E在同一条直线上,连接DC .
(1)、当D点在伞柄上滑动时,处于同一平面的两条伞骨和相等吗?请说明理由.(2)、如图③,当油纸伞撑开时,伞的边缘M , N与点D在同一直线上,若 , , 求的度数.20. 两个大小不同的等腰直角三角板如图所示放置,右图是由它抽象出的几何图形,B , C , E在同一条直线上,连接DC .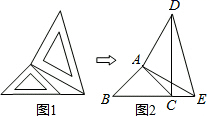 (1)、求证:△ABE≌△ACD;(2)、若图2中的BE=3CE , CD=6,求 △DCE的面积.21. 如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)、求证:△ABE≌△ACD;(2)、若图2中的BE=3CE , CD=6,求 △DCE的面积.21. 如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC. (1)、求证:△ABD≌△EDC;(2)、若AB=2,BE=3,求CD的长.22. 如图,在 中,按以下步骤作图:
(1)、求证:△ABD≌△EDC;(2)、若AB=2,BE=3,求CD的长.22. 如图,在 中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交BA,BC于点M,N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.请你观察图形,解答下列问题.
(1)、由尺规作图可证得 ,依据是;(2)、求证: ;(3)、若 , ,求∠ACB的度数.23. [阅读理解]课外兴趣小组活动时,老师提出了如下问题:如图1,在中,若 , 求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD到点E , 使 , 连结BE , 请根据小明的方法思考:
图1
 图2
图2  图3
图3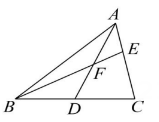 (1)、由已知和作图能得到 , 其理由是什么?(2)、求AD的取值范围.(3)、如图3,AD是的中线,BE交AC于点F , 且 , 试说明 .24. 在直线m上依次取互不重合的三个点D , A , E , 在直线m上方有 , 且满足 .(1)、【积累经验】
(1)、由已知和作图能得到 , 其理由是什么?(2)、求AD的取值范围.(3)、如图3,AD是的中线,BE交AC于点F , 且 , 试说明 .24. 在直线m上依次取互不重合的三个点D , A , E , 在直线m上方有 , 且满足 .(1)、【积累经验】如图1,当时,猜想线段DE , BD , CE之间的数量关系是;
 (2)、【类比迁移】
(2)、【类比迁移】如将2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;
 (3)、【拓展应用】
(3)、【拓展应用】如图3,在中,是钝角, , , , 直线m与CB的延长线交于点F , 若 , 的面积是12,请直接写出与的面积之和.
