浙教版数学八年级上册《第1章三角形的初步知识》单元同步测试卷

试卷更新日期：2024-08-06 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下面四个图形中，线段 $B E$ 能表示 $△ A B C$ 的高的是（）

A、 B、 C、 D、

查看试题解析
2. 在Rt△ABC中，若一个锐角等于40°，则另一个锐角的度数为（　　）

A、40° B、45° C、50° D、60°

查看试题解析
3. 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）

A、16 B、11 C、3 D、6

查看试题解析
4. 下列语句中，不是命题的是（　　）

A、两点确定一条直线 B、垂线段最短 C、作角A的平分线 D、内错角相等

查看试题解析
5. 如图， $D E / / B C ， B E$ 平分 $∠ A B C$ ，求证： $∠ 1 =$ $∠ 3$ .以下是排乱的证明过程：
① $∵ D E / / B C$ (已知)，
② $∵ B E$ 平分 $∠ A B C$ (已知)，
③ $∴ ∠ 1 = ∠ 2$ (角平分线的定义)，
④ $∴ ∠ 2 = ∠ 3$ (两直线平行，同位角相等)，
⑤ $∴ ∠ 1 = ∠ 3$ (等量代换).
证明步㵵顺序正确的是（）

A、③ $\to$ ② $\to$ ① $\to$ ④ $\to$ ⑤ B、① $\to$ ④ $\to$ ② $\to$ ③ $\to$ ⑤ C、① $\to$ ③ $\to$ ④ $\to$ ② $\to$ ⑤ D、① $\to$ ④ $\to$ ③ $\to$ ② $\to$ ⑤

查看试题解析
6. 如图，观察图中的尺规作图痕迹，下列说法错误的是（）

A、 $∠ D A E = ∠ B$ B、 $∠ C = ∠ E A C$ C、 $∠ D A E = ∠ E A C$ D、 $A E / / B C$

查看试题解析
7. 已知图中的两个三角形全等，则∠α的度数是（）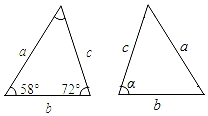

A、72° B、60° C、58° D、50°

查看试题解析
8. 如图，嘉淇利用全等三角形的知识测量池塘两端A，B之间的距离，如果△AOB≌△COD，则只需测出（）

A、OD的长度 B、CD的长度 C、OB的长度 D、AC的长度

查看试题解析
9. 如图，已知 $A C = A D$ ，再添加一个条件仍不能判定 $Δ A B C ≅ Δ A B D$ 的是（）

A、 $∠ C = ∠ D = 90 °$ B、 $∠ B A C = ∠ B A D$ C、 $B C = B D$ D、 $∠ A B C = ∠ A B D$

查看试题解析
10. 如图，在△ABC中，AB=4，AC=5，以点A为圆心，任意长为半径画弧，分别交AB，AC于点D和E，再分别以点D，E为圆心，大于 $\frac{1}{2}$ DE长为半径画弧，两弧交于点F，连接AF并延长交BC于点M，作MN⊥AC于点N．若MN=2，则△ABM的面积为（）

A、4 B、5 C、8 D、10

查看试题解析

二、填空题（每题3分，共18分）

11. 等腰三角形的一边长等于4，一边长等于9，它的周长是.

查看试题解析
12. 将命题“对顶角相等”改写成“如果……，那么……”的形式：.

查看试题解析
13. 如图，若 $△ A B C ≌ △ D E F$ ， $B E = 3$ ， $A E = 8$ ，则 $B D$ 的长是．

查看试题解析
14. 如图，电线杆上的横梁下方用三角形的支架支撑的理论根据是.

查看试题解析
15. 已知： $∠ A O B$ ．求作： $∠ A O B$ 的平分线．
作法：（1）以点 $O$ 为圆心，适当长为半径画弧，交 $O A$ 于点 $M$ ，交 $O B$ 于点 $N$ ；（2）分别以点 $M$ ， $N$ 为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧在 $∠ A O B$ 的内部相交于点 $P$ ；（3）画射线 $O P$ ，射线 $O P$ 即为所求（如图）．
从上述作法中可以判断 $△ M O P ≌ △ N O P$ ，其依据是（在“SSS”“SAS”“AAS”“ASA”中选填）

查看试题解析
16. 如图，①在OA、OB上分别截取线段OD、OE ，使OD=OE；②分别以 $D ， E$ 为圆心，大于 $\frac{1}{2} D E$ 的长为半径画弧，在 $∠ A O B$ 内两弧交于点 $C$ ；③作射线 $O C$ ．若∠AOB=60° ，则 $∠ A O C =$ $°$ ．

查看试题解析

三、解答题（共9题，共72分）

17. 已知：如图， $A B / / D C$ ， $A C$ 和 $B D$ 相交于点 $O$ ， $E$ 是 $C D$ 上一点， $F$ 是 $O D$ 上一点，
且 $∠ 1 = ∠ A$ ．

(1)、求证： $F E / / O C$ ；

(2)、若 $∠ B F E = 110 °$ ， $∠ 1 = 60 °$ ，求 $∠ B$ 的度数．

查看试题解析
18. 已知：如图，点A、B、C、D在一条直线上， $E A / / F B ， E A = F B ， A B = C D$ .

(1)、求证： $△ A C E ≌ △ B D F$ ；

(2)、若 $∠ A = 40 ， ∠ D = 80 °$ ，求 $∠ E$ 的度数.

查看试题解析
19. 如图，在△ABC中，∠B=∠C，过BC的中点D作DE⊥AB，DF⊥AC，垂足分别为点E、F.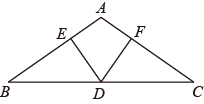

(1)、求证∶DE=DF；

(2)、若∠BDE=55°，求∠BAC的度数.

查看试题解析
20. 如图，已知△ABF≌△CDE.

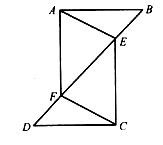(1)、若∠B＝30°，∠DCF＝40°，求∠EFC的度数；

(2)、若BD=10，EF=2，求BF的长.

查看试题解析
21. 如图， $R t Δ A B C$ 和 $R t Δ A D E$ 中， $∠ C = ∠ E = 90 °$ ， $∠ C A D = ∠ E A B$ ， $A C = A E$ ，AB，DE相交于点F，AD，BC相交于点G.

(1)、求证： $Δ A B C ≅ Δ A D E$ ；

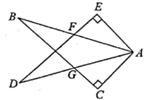(2)、若 $A B = 11$ ， $A G = 6$ ，求DG的长.

查看试题解析
22. 如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．

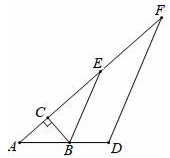(1)、求∠CBE的度数；

(2)、过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．

查看试题解析
23. 如图，在Rt△ABC中，∠C=90°.

(1)、作∠BAC的平分线AD交边BC于点D.（尺规作图，保留作图痕迹，不写作法）.

(2)、在（1）的条件下，若∠BAC=28°，求∠ADB的度数.

查看试题解析
24. 在 $R t △ A B C$ 中， $∠ B A C = 90 ° ， A B = A C$ ，过直角顶点 $A$ 作直线 $M N ， B D ⊥ M N$ 于点 $D ， C E ⊥ M N$ 于点 $E$ ．

(1)、如图1，当 $M N$ 与 $B C$ 边不相交时，判断 $B D ， C E ， D E$ 之间的数量关系，并说明理由；

(2)、当 $M N$ 与边 $B C$ 相交时，请在图2中画出图形，并直接写出 $B D ， C E ， D E$ 之间的数量关系．

查看试题解析
25. [问题情境]
在综合实践课上，老师组织班上的同学开展了探究两角之间数量关系的数学活动，如题24图，已知射线AM∥BN，连接AB，点P是射线AM上的一个动点(与点A不重合)，BC，BD分别平分∠ABP和∠PBN，且分别交射线AM于点C，D．
[探索发现]

(1)、当∠A=60°时，求证：∠CBD=∠A．

(2)、”快乐小组”经过探索后发现：不断改变∠A的度数，∠CBD与∠A始终存在某种数量关系．
①当∠A=40°时，∠CBD=度；
②当∠A=x°时，∠CBD=度(用含x的代数式表示)．

(3)、[操作探究]
”智慧小组”利用量角器量出∠APB和∠ADB的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线AM上运动时，无论点P在AM上的什么位置，∠APB与∠ADB之间的数量关系都保持不变．请写出它们的关系，并说明理由．

查看试题解析

浙教版数学八年级上册《第1章 三角形的初步知识》单元同步测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

浙教版数学八年级上册《第1章三角形的初步知识》单元同步测试卷