浙教版数学九年级上册《第1章 二次函数》单元同步测试卷
试卷更新日期:2024-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列函数中,y是x的二次函数的是( )A、y=3x B、y=- C、y=+5 D、y=x2-3x+52. 已知函数是二次函数,则等于( )A、 B、2 C、 D、63. 若抛物线y=x2+bx+c的对称轴为y轴,且点P(2,6)在该抛物线上,则c的值为( )A、﹣2 B、0 C、2 D、44. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、
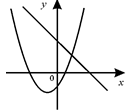 B、
B、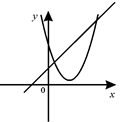 C、
C、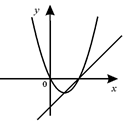 D、
D、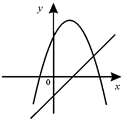 5. 已知二次函数的图象如图所示,给出以下结论:①;②;③;④;⑤ , 其中正确结论是( )
5. 已知二次函数的图象如图所示,给出以下结论:①;②;③;④;⑤ , 其中正确结论是( ) A、②③④ B、②③⑤ C、①②⑤ D、①③⑤6. 把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、7. 函数与的图象如图所示,当( )时, , 均随着的增大而减小.
A、②③④ B、②③⑤ C、①②⑤ D、①③⑤6. 把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、7. 函数与的图象如图所示,当( )时, , 均随着的增大而减小. A、 B、 C、 D、8. 若二次函数的部分图象如图所示,则关于的方程的解为( )
A、 B、 C、 D、8. 若二次函数的部分图象如图所示,则关于的方程的解为( ) A、 , B、 , C、 , D、 ,9. 已知二次函数的图象如图所示,下列说法错误的是( )
A、 , B、 , C、 , D、 ,9. 已知二次函数的图象如图所示,下列说法错误的是( ) A、图象关于直线对称 B、函数的最小值是-4 C、当时,y随x的增大而增大 D、-1和3是方程的两个根10. 已知抛物线y=ax2+bx+c开口向下,顶点坐标(3,-5),那么该抛物线有( )A、最小值-5 B、最大值-5 C、最小值3 D、最大值3
A、图象关于直线对称 B、函数的最小值是-4 C、当时,y随x的增大而增大 D、-1和3是方程的两个根10. 已知抛物线y=ax2+bx+c开口向下,顶点坐标(3,-5),那么该抛物线有( )A、最小值-5 B、最大值-5 C、最小值3 D、最大值3二、填空题(每题3分,共18分)
-
11. 已知抛物线y=x2-6x+m与x轴有且只有一个交点,则m=.12. 将抛物线先向右平移2个单位长度,再向上平移3个单位长度,得到的抛物线是 .13. 抛物线 的顶点坐标是 .14. 已知二次函数y=ax2+bx+c的函数值y与自变量x的部分对应值如表:
x
…
﹣2
﹣1
0
1
2
3
…
y
…
8
3
0
﹣1
0
3
…
则这个二次函数图象的对称轴是直线 .
15. 请你写出一个二次函数,其图象满足条件:①开口向下;②与 轴的交点坐标为 .此二次函数的解析式可以是16. 如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 则铅球被推出的水平距离为 m.
三、解答题(共8题,共72分)
-
17. 已知一次函数和二次函数 , 下表给出了与自变量的几组对应值:
…
0
1
2
3
4
…
…
5
4
3
2
1
0
…
…
0
3
4
3
0
…
(1)、求的解析式;(2)、直接写出关于的不等式的解集.18. 如图,二次函数y=x2+bx+c的图象与x轴交于A(-1,0)、B(3,0)两点,顶点为D. (1)、求此二次函数的解析式;(2)、求△ABD的面积.19. 如图,在矩形中, , , 点M从A出发 , 以的速度在矩形边上沿A→B→C方向运动,点N从B点出发,以的速度在矩形边上沿B→C→D方向运动,两点同时出发,其中一点到达终点时,两点同时停止,运动时间为t(单位:s , 且0<t≤6).
(1)、求此二次函数的解析式;(2)、求△ABD的面积.19. 如图,在矩形中, , , 点M从A出发 , 以的速度在矩形边上沿A→B→C方向运动,点N从B点出发,以的速度在矩形边上沿B→C→D方向运动,两点同时出发,其中一点到达终点时,两点同时停止,运动时间为t(单位:s , 且0<t≤6).
 (1)、当0<t≤4时,能否成为等腰三角形,若能,求出此时t的值,若不能,说明理由;(2)、如图,当4<t≤6时,恰好是以BN为底的等腰三角形,求此时t的值.20. 如图,已知抛物线y=﹣x2+mx+3经过点M(﹣2,3).
(1)、当0<t≤4时,能否成为等腰三角形,若能,求出此时t的值,若不能,说明理由;(2)、如图,当4<t≤6时,恰好是以BN为底的等腰三角形,求此时t的值.20. 如图,已知抛物线y=﹣x2+mx+3经过点M(﹣2,3).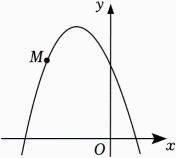 (1)、求m的值,并求出此抛物线的顶点坐标;(2)、当﹣3≤x≤0时,直接写出y的取值范围.21. 绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示.
(1)、求m的值,并求出此抛物线的顶点坐标;(2)、当﹣3≤x≤0时,直接写出y的取值范围.21. 绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示. (1)、求生产成本y2(元)与产量x(kg)之间的函数关系式;(2)、求日利润为W(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?22. 从地面竖直向上发射的物体离地面的高度满足关系式 , 其中是物体运动的时间,是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.(1)、小球被发射后s时离地面的高度最大(用含的式子表示).(2)、若小球离地面的最大高度为20m,求小球被发射时的速度.(3)、按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s.”已知实验楼高15m,请判断他的说法是否正确,并说明理由.23. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).
(1)、求生产成本y2(元)与产量x(kg)之间的函数关系式;(2)、求日利润为W(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?22. 从地面竖直向上发射的物体离地面的高度满足关系式 , 其中是物体运动的时间,是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.(1)、小球被发射后s时离地面的高度最大(用含的式子表示).(2)、若小球离地面的最大高度为20m,求小球被发射时的速度.(3)、按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s.”已知实验楼高15m,请判断他的说法是否正确,并说明理由.23. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).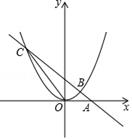 (1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.24. 根据以下素材,探索完成任务.
(1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.24. 根据以下素材,探索完成任务.如何设计喷泉安全通道?
在抛物线形的喷泉水柱下设置一条安全的通道,可以让儿童在任意时间穿过安全通道时不被水柱喷到(穿梭过程中人的高度变化忽略不计).
素材1
图1为音乐喷泉,喷头的高度在垂直地面的方向上随着音乐变化而上下移动.不同高度的喷头喷出来的水呈抛物线型或抛物线的一部分,但形状相同,最高高度也相同,水落地点都在喷水管的右侧.

素材2
图2是当喷水头在地面上时(喷水头最低),其抛物线形水柱的示意图,水落地点离喷水口的距离为 , 水柱最高点离地面 .
图3是某一时刻时,水柱形状的示意图.为喷水管,为水的落地点,记长度为喷泉跨度.


素材3
安全通道在线段上,若无论喷头高度如何变化,水柱都不会进入上方的矩形区域,则称这个矩形区域为安全区域.

问题解决
任务1
确定喷泉形状.
在图2中,以为原点,所在直线为轴,建立平面直角坐
标系,求出抛物线的函数表达式.
任务2
确定喷泉跨度的最小值.
若喷水管最高可伸长到 , 求出喷泉跨度的最小值.
任务3
设计通道位置及儿童的身高上限.
现在需要一条宽为的安全通道 , 为了确保进入安全通道
上的任何人都能在安全区域内,则能够进入该安全通道的人
的最大身高为多少?(精确到)