北师大版数学九年级上册《第一章 特殊平行四边形》单元提升测试卷
试卷更新日期:2024-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在中, , 相交于点 , , . 过点作的垂线交于点 , 记长为 , 长为 . 当 , 的值发生变化时,下列代数式的值不变的是( )
 A、 B、 C、 D、2. 如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE , AF , AM平分∠EAF交CD于点M . 若BE=DF=1,则DM的长度为( )
A、 B、 C、 D、2. 如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE , AF , AM平分∠EAF交CD于点M . 若BE=DF=1,则DM的长度为( ) A、2 B、 C、 D、3. 如图,在正方形中,是上一点, , , 若是上一动点,则的最小值是( )
A、2 B、 C、 D、3. 如图,在正方形中,是上一点, , , 若是上一动点,则的最小值是( ) A、12 B、10 C、8 D、164. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )
A、12 B、10 C、8 D、164. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )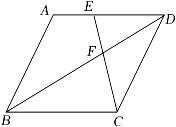 A、16 B、6 C、12 D、305. 如图,矩形的对角线 , 相交于点O , , , 点M , N分别是 , 的中点,连接 , 若四边形的周长是16,则的长为( )
A、16 B、6 C、12 D、305. 如图,矩形的对角线 , 相交于点O , , , 点M , N分别是 , 的中点,连接 , 若四边形的周长是16,则的长为( ) A、1 B、2 C、4 D、86. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为边作矩形 . 动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A、1 B、2 C、4 D、86. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为边作矩形 . 动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )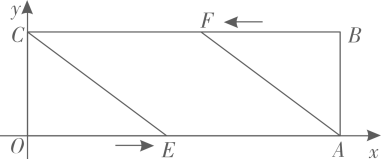 A、 B、 C、 D、7. 如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
A、 B、 C、 D、7. 如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A、① B、①② C、①③ D、①②③8. 如图,正方形由四个全等的直角三角形( , , , )和中间一个小正方形组成,连接 . 若 , , 则( ) A、5 B、 C、 D、49. 如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A、5 B、 C、 D、49. 如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( ) A、 B、 C、1 D、10. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF , AE、BF相交于点O , 下列结论:
A、 B、 C、1 D、10. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF , AE、BF相交于点O , 下列结论:
①AE=BF;②AE⊥BF;③AO=OE;④中正确的有( )
A、4个 B、3个 C、2个 D、1个二、填空题(每题3分,共18分)
-
11. 如图,在菱形中,对角线 , 相交于点 , . 线段与关于过点的直线对称,点的对应点在线段上,交于点 , 则与四边形的面积比为 .
 12. 如图,四边形是矩形,是正三角形,点F是的中点,点P是矩形内一点,且是以为底的等腰三角形,则的面积与的面积的比值是.
12. 如图,四边形是矩形,是正三角形,点F是的中点,点P是矩形内一点,且是以为底的等腰三角形,则的面积与的面积的比值是. 13. 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则 = .
13. 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则 = . 14. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
14. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°. 15. 如图,在矩形中,点E在边上,点F是AE的中点, , 则的长为 .
15. 如图,在矩形中,点E在边上,点F是AE的中点, , 则的长为 . 16. 如图,点E是正方形内的一点,将绕点B按顺时针方向旋转得到 . 若 , 则度.
16. 如图,点E是正方形内的一点,将绕点B按顺时针方向旋转得到 . 若 , 则度.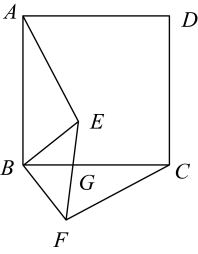
三、解答题(共7题,共72分)
-
17. 如图,为菱形的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹)
 (1)、如图,过点作的垂线;(2)、如图 , 点为线段的中点,过点作的平行线.18. 如图,在矩形ABCD中,对角线AC , BD交于点O , 分别过点C , D作BD , AC的平行线交于点E , 连接OE交AD于点F .
(1)、如图,过点作的垂线;(2)、如图 , 点为线段的中点,过点作的平行线.18. 如图,在矩形ABCD中,对角线AC , BD交于点O , 分别过点C , D作BD , AC的平行线交于点E , 连接OE交AD于点F . (1)、求证:四边形OCED是菱形;(2)、若AB=5,∠BOC=120°,求菱形OCED的周长.19. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)、求证:四边形OCED是菱形;(2)、若AB=5,∠BOC=120°,求菱形OCED的周长.19. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. (1)、线段BD与CD有什么数量关系,并说明理由;(2)、当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.20. 康康在学习了矩形定义及判定定理1后,继续探究其它判定定理.(1)、实践与操作
(1)、线段BD与CD有什么数量关系,并说明理由;(2)、当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.20. 康康在学习了矩形定义及判定定理1后,继续探究其它判定定理.(1)、实践与操作
①任意作两条相交的直线,交点记为O;
②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段;OA , OB , OC , OD
③顺次连结所得的四点得到四边形.
于是可以直接判定四边形是平行四边形,则该判定定理是:.
(2)、猜想与证明通过和同伴交流,他们一致认为四边形是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.
已知:如图,四边形是平行四边形,.

求证:四边形是矩形.
21. 【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点,AE⊥EP , EP与正方形的外角∠DCG的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;
 (1)、【思考尝试】:
(1)、【思考尝试】:同学们发现,取AB的中点F , 连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
(2)、【实践探究】:希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E , B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接CP , 可以求出∠DCP的大小,请你思考并解答这个问题.
22. 如图,在正方形中,E、F分别是边、上的两点,且 , 、分别交正方形的对角线于G、H两点,将绕点A顺时针旋转90°后,得到 , 连接 . (1)、求证:平分;(2)、求证:;(3)、试试探索、 、三条线段间的数量关系,并加以证明.23. 综合与实践
(1)、求证:平分;(2)、求证:;(3)、试试探索、 、三条线段间的数量关系,并加以证明.23. 综合与实践问题情境:在综合与实践课上,老师让同学们以“矩形纸片的折叠”为主题开展数学活动,请你解答各小组活动中产生的问题如图所示,在矩形中, , , 将矩形纸片进行折叠:
 (1)、问题解决:如图 , 奋斗小组将该矩形沿对角线折叠,点的对应点为点 , 则 , ;(2)、实践探究:如图 , 希望小组将矩形沿着点 , 分别在边 , 边上所在的直线折叠,点的对应点为点 , 连接 ,
(1)、问题解决:如图 , 奋斗小组将该矩形沿对角线折叠,点的对应点为点 , 则 , ;(2)、实践探究:如图 , 希望小组将矩形沿着点 , 分别在边 , 边上所在的直线折叠,点的对应点为点 , 连接 ,试判断四边形的形状,并说明理由;
求折痕的长.