北师大版数学九年级上册《第一章 特殊平行四边形》单元同步测试卷
试卷更新日期:2024-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,以点A为圆心,适当的长为半径画弧,交两边于点M , N , 再分别以M、N为圆心,的长为半径画弧,两弧交于点B , 连接 . 若 , 则( )
 A、 B、 C、 D、2. 中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴,小陶家有一个菱形中国结装饰.测得 . 则该菱形的面积为( )
A、 B、 C、 D、2. 中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴,小陶家有一个菱形中国结装饰.测得 . 则该菱形的面积为( ) A、 B、 C、 D、3. 如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,则OE的长等于( )
A、 B、 C、 D、3. 如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,则OE的长等于( )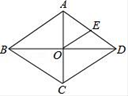 A、2 B、3.5 C、7 D、144. 如图,在矩形中,对角线与相交于点 , 则下列结论一定正确的是( )
A、2 B、3.5 C、7 D、144. 如图,在矩形中,对角线与相交于点 , 则下列结论一定正确的是( ) A、 B、 C、 D、5. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、对角线相等的四边形是矩形 D、四条边都相等的四边形是菱形6. 如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其推理依据是( )
A、 B、 C、 D、5. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、对角线相等的四边形是矩形 D、四条边都相等的四边形是菱形6. 如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其推理依据是( ) A、矩形的对角线相等 B、矩形的四个角是直角 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是矩形7. 正方形具备而矩形不具备的性质是( )A、四条边都相等 B、四个角都是直角 C、对角线互相平分 D、对角线相等8. 如图,点在正方形的内部,且在对角线的上方,连接、 , 若 , 则的度数为( )
A、矩形的对角线相等 B、矩形的四个角是直角 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是矩形7. 正方形具备而矩形不具备的性质是( )A、四条边都相等 B、四个角都是直角 C、对角线互相平分 D、对角线相等8. 如图,点在正方形的内部,且在对角线的上方,连接、 , 若 , 则的度数为( ) A、 B、 C、 D、9. 如图,在正方形的外侧,作等边 , 则为( )
A、 B、 C、 D、9. 如图,在正方形的外侧,作等边 , 则为( ) A、 B、 C、 D、10. 如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A、 B、 C、 D、10. 如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )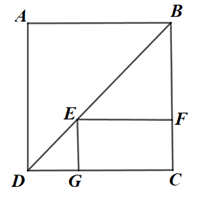 A、4 B、8 C、16 D、32
A、4 B、8 C、16 D、32二、填空题(每题3分,共18分)
-
11. 如图,在矩形中对角线 , 交于点 , 请添加一个条件 , 使矩形是正方形(填一个即可)
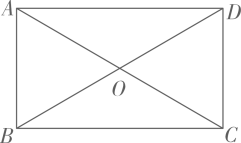 12. 如图,已知点O是矩形ABCD的对称中心,E、F分别是边AD、BC上的点,且关于点O中心对称,如果矩形的面积是22,那么图中阴影部分的面积是.
12. 如图,已知点O是矩形ABCD的对称中心,E、F分别是边AD、BC上的点,且关于点O中心对称,如果矩形的面积是22,那么图中阴影部分的面积是. 13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .
13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .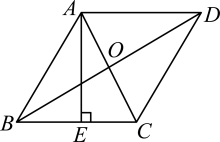 14. 如图,菱形ABCD的周长16cm,则菱形ABCD的一边中点E到对角线交点O的距离为.cm.
14. 如图,菱形ABCD的周长16cm,则菱形ABCD的一边中点E到对角线交点O的距离为.cm.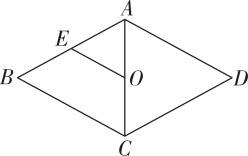 15. 如图,在矩形ABCD中, , , 作AE平分∠BAD , 若连接BF , 则BF的长度为。
15. 如图,在矩形ABCD中, , , 作AE平分∠BAD , 若连接BF , 则BF的长度为。 16. 如图,连接四边形ABCD各边中点,得到四边形EFGH , 只要添加条件ACBD . 就能保证四边形EFGH是菱形.
16. 如图,连接四边形ABCD各边中点,得到四边形EFGH , 只要添加条件ACBD . 就能保证四边形EFGH是菱形.
三、解答题(共8题,共72分)
-
17. 如图,在中,已知 , , 与交于点 , 且 .
 (1)、试判断四边形的形状,并说明理由.(2)、若 , 且 , , 求的长.18. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)、试判断四边形的形状,并说明理由.(2)、若 , 且 , , 求的长.18. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.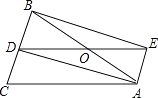 (1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由19. 如图,菱形ABCD的对角线AC、BD相交于点O, , ,OE与AB交于点F.
(1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由19. 如图,菱形ABCD的对角线AC、BD相交于点O, , ,OE与AB交于点F. (1)、求证:四边形AEBO的为矩形;(2)、若OE=10,AC=16,求菱形ABCD的面积.20. 如图,在平行四边形中,过点作于点 , 点在边上,且 , 连接 , .
(1)、求证:四边形AEBO的为矩形;(2)、若OE=10,AC=16,求菱形ABCD的面积.20. 如图,在平行四边形中,过点作于点 , 点在边上,且 , 连接 , .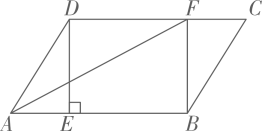 (1)、求证:四边形是矩形;(2)、若平分 , , , 求的长.21. 如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)、求证:四边形是矩形;(2)、若平分 , , , 求的长.21. 如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF. (1)、求证:▱ABCD是菱形;(2)、若AB=5,AC=6,求▱ABCD的面积.22. 王华同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.
(1)、求证:▱ABCD是菱形;(2)、若AB=5,AC=6,求▱ABCD的面积.22. 王华同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在平行四边形ABCD中, , 求证:平行四边形ABCD是 .
(1)、在方框中填空,以补全已知和求证;(2)、按王晓的想法写出证明过程;证明:
23. 如图,点E是正方形ABCD内的一点,将△BEC绕点C顺时针旋转至△DFC.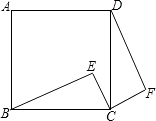 (1)、请问最小旋转度数为多少?
(1)、请问最小旋转度数为多少?
(2)、指出图中的全等图形以及它们的对应角?
(3)、若∠EBC=30°,∠BCE=80°,求∠F的度数.24.如图,四边形ABCD是正方形,点E在直线BC上,连接AE.将△ABE沿AE所在直线折叠,点B的对应点是点B' , 连接AB'并延长交直线DC于点F.
 (1)、当点F与点C重合时如图(1),易证:DF+BE=AF(不需证明);(2)、当点F在DC的延长线上时如图(2),当点F在CD的延长线上时如图(3),线段DF、BE、AF有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.
(1)、当点F与点C重合时如图(1),易证:DF+BE=AF(不需证明);(2)、当点F在DC的延长线上时如图(2),当点F在CD的延长线上时如图(3),线段DF、BE、AF有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.