北师大版数学八年级上册《第一章 勾股定理》单元提升测试卷
试卷更新日期：2024-08-06 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 如图，在5×5的正方形网格中，从在格点上的点A ， B ， C ， D中任取三点，所构成的三角形恰好是直角三角形的个数为（ ）
A、3 B、2 C、1 D、02. 如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D'处，若AB=3，AD=4，则ED的长为（ ）
A、 B、3 C、1 D、3. 下列各组数中不是勾股数的是（ ）A、9，15，12 B、11，60，61 C、6，8，10 D、0.3，0.4，0.54. 如图，在正方形网格中，每个小正方形的边长都是1，四条线段，其中能组成直角三角形三边的一组线段是（ ）
A、 B、 C、 D、5. 如图，有一个绳索拉直的木马秋千，绳索AB的长度为5米.若将它往水平方向向前推进3米（即DE=3米），且绳索保持拉直的状态，则此时木马上升的高度为（ ）
A、1米 B、米 C、2米 D、4米6. 如图，由四个全等的直角三角形与中间的小正方形拼成的大正方形图案是某届国际数学大会的会标，如果大正方形的面积为16，小正方形的面积为3，直角三角形的两直角边分别为a和b，那么 的值为（ ）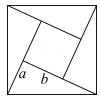
A、256 B、169 C、29 D、487. 如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，若知道图中阴影部分的面积，则一定能求出（ ）
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和8. 小强家因装修准备用电梯搬运一些木条上楼，如图，已知电梯的长、宽、高分别是 ， ， ， 那么电梯内能放入下列木条中的最大长度是（ ）
A、 B、 C、 D、9. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃（读kǔn，门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图1、2（图2为图1的平面示意图），推开双门，双门间隙CD的距离为2寸，点C和点D距离门槛AB都为1尺（1尺＝10寸），则AB的长是（ ）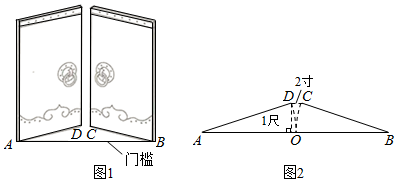
A、50.5寸 B、52寸 C、101寸 D、104寸10. 华表柱是一种中国传统建筑形式，天安门前耸立着高大的汉白玉华表，每根华表重约20000公斤，如图，在底面周长约为3米带有层层回环不断的云朵石柱上，有一条雕龙从柱底向柱顶（从点到点）均匀地盘绕3圈，每根华表刻有雕龙部分的柱身高约9米，则雕刻在石柱上的巨龙至少（ ）米.
A、 B、 C、 D、二、填空题（每题3分，共18分）
-
11. 如图，阴影部分是两个正方形，其他三个图形是一个正方形和两个直角三角形，则阴影部分的面积之和为.
12. 如图，长方形 ABCD 中，点 E 在边 AB 上，将一边 AD 折叠，使点 A恰好落在边 BC 的点 F 处，折痕为 DE．若 AB=4，BF=2，则 AE的长是 ．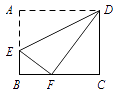
13. 如图是一个三级台阶，它的每一级的长、宽、高分别为 ， 和 ， 和 是这个台阶的两个端点， 点上有一只蚂蚁想到 点去吃可口的食物，则它所走的最短路线长度为 .
14. 对角线互相垂直的四边形叫做“垂美”四边形，如图所示的“垂美”四边形的对角线 ， 交于点 ， 若 ， ， 则＝ ．
15. 在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的大意是：如图，有一个水池，水面是一个边长为10尺的正方形．在水池正中央有一根新生的芦苇，它高出水面1尺．如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，则这个水池的深度是尺．
16. 如图，已知AP平分∠BAC ， PD⊥AB于D ， PC⊥AC于C ， 且PB＝PE.其中AC=16，AB=21，PB=13，则PC=.
三、解答题（共8题，共72分）
-
17. “儿童散学归来早，忙趁东风放纸鸢”又到了放风筝的最佳时节．某校八年级班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度 ， 他们进行了如下操作：测得水平距离的长为米；根据手中剩余线的长度计算出风筝线的长为米；牵线放风筝的小明的身高为米．
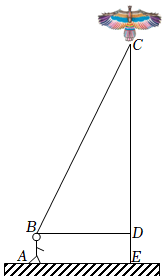(1)、求风筝的垂直高度；(2)、如果小明想风筝沿方向下降米，则他应该往回收线多少米？18. 如图，一辆小汽车在一段限速高速公路上沿直道行驶，某一时刻刚好行驶到路对面车速检测仪的正前方的处，过了后，测得小汽车到达与车速检测仪之间的距离为的处．
(1)、你能计算这辆小汽车的速度吗？(2)、这辆小汽车超速了吗？19. 已知：在线段的同侧分别过A、B作 ， ， 分别在射线 ， 上取点C、D.若 ， ， 点P是线段上的一个动点.
(1)、如图1，连接、 ， 当且时，求的长；(2)、如图2，点P在线段上以2个单位每秒的速度从点B向点A运动，同时点Q在射线上以x个单位每秒的速度从A点开始运动，当点P到达A点时停止运动.①连接 ， 当时，求x的值；
②是否存在实数x的值，使得某时刻与全等？若存在，请你求出x的值；若不存在，请说明理由.
20. 已知如下数表：n
2
3
4
5
……
a
22-1
32-1
42-1
52-1
……
b
4
6
8
10
……
c
22+1
32+1
42+1
52+1
……
(1)、观察a，b，c与n之间的关系，用含自然数n（n>1）的代数式表示：a= ， b= ， c= ．(2)、试猜想：以a，b，c为边的三角形是直角三角形吗？请说明理由．21. 定义：在任意中，如果一个内角度数的2倍与另一个内角度数的和为 ， 那么称此三角形为“倍角互余三角形”.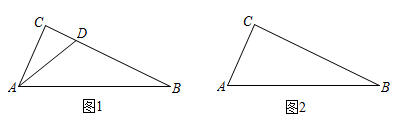
(1)、【基础巩固】若是“倍角互余三角形”， ， ， 则；(2)、【尝试应用】如图1，在中， ， 点为线段上一点，若与互余.求证：是“倍角互余三角形”；(3)、【拓展提高】如图2，在中， ， ， ， 试问在边上是否存在点 ， 使得是“倍角互余三角形”？若存在，请求出的长；若不存在，请说明理由.22. 在一款名为超级玛丽的游戏中，玛丽到达一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，
(1)、求高台A比矮台B高多少米？
(2)、求旗杆的高度OM；
(3)、玛丽在荡绳索过程中离地面的最低点的高度MN．
23. 为了测量学校旗杆的高度，八(1)班的两个数学研究小组设计了不同的方案，请结合下面表格的信息，完成任务问题．测量旗杆的高度
测量工具
测量角度的仪器、皮尺等
测量小组
第一小组
第二小组
测量方案示意图
设计方案及测量数据
在地面确定点C，并测得旗杆顶端A的仰角，即∠ACB=45°．
如图1，绳子垂直挂下来时，相比旗杆，测量多出的绳子长度FP为2米．如图2，绳子斜拉直后至末端点P位置，测量点P到地面的距离PD为1米，以及点P到旗杆AB的距离PE为9米．
(1)、任务一：判断分析第一小组要测旗杆AB的高度，只需要测量 的长度为线段并说明理由．
(2)、任务二：推理计算利用第二小组获得的数据，求旗杆的高度AB．
24. 在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D落在点F处.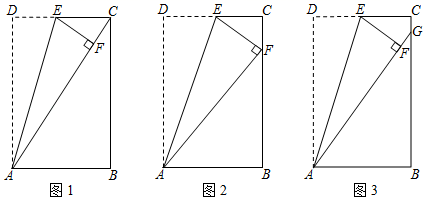
(1)、如图1，若点F落在对角线AC上，且∠BAC＝54°，则∠DAE的度数为°.(2)、如图2，若点F落在边BC上，且AB＝6，AD＝10，求CE的长.(3)、如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB＝6，AD＝10，求CG的长.